
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Нормальный закон распределения
Он характеризует вероятность отказа при длительном изменении характеристик изделия (старение, износ). Нормальный закон распределения характеризует распределение времени безотказной работы изделия при возникновении отказов из-за износа и старения.
Плотность распределения времени безотказной работы Tизделия равна:
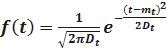 ,
,
Гдеmt, Dt – параметры закона распределения.
mt– среднее значение случайной величины T;
Dt – дисперсия случайной величины T;
Имеем
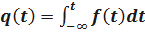 ;
; 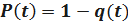 ;
; 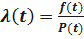 ;
;
Для нормального закона распределения q(t) примет вид
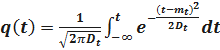 .
.
Введём новую переменную:
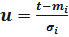 ;
;  ;
; 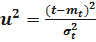 .
.
Если 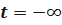 ,то
,то 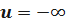 .
.
Следовательно
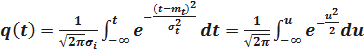 .
.
Введём в рассмотрение нормированную функцию Лапласа
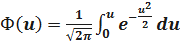 ,
, 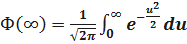 ,
,
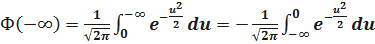 .
.
Свойства функции Лапласа
1) Ф(0) = 0;
2) Ф(-u) = -Ф(u);
3) 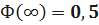 .
.
Запишем q(t) в виде
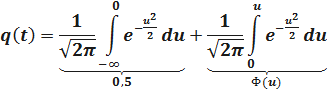
 ;
; 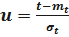 ;
;
Определим вероятность безотказной работы изделия в интервале времени (t, t1)
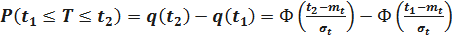 .
.
Определим интенсивность отказов 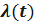 . Имеем
. Имеем
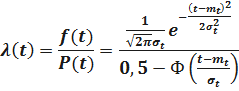
Определим P(t, t1) – время безотказной работы изделия на интервале времени (t, t1) при условии, что на интервале времени (0, t) изделие работало безотказно. Имеем
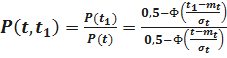 ;
;
1.16.3 Закон распределения Вейбулла
Для распределения Вейбулла плотность распределения времени безотказной работы Т изделия имеет вид
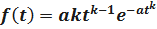 ;
;
здесь aи k– параметры закона распределения Вейбулла.
Определим q(t). Имеем
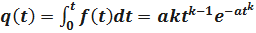 .
.
Введём новую переменную x вида
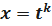 ;
; 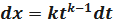 ;
;
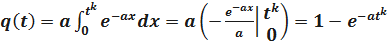 ;
; 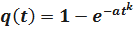
Определим P(t). Имеем
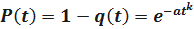 ;
; 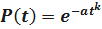
Определим 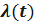 . Получим
. Получим
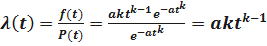 .
.
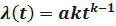 .
.
Определим среднее время безотказной работы. Имеем
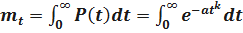 .
.
Введём новую переменную uвида
 ;
; 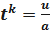 ;
; 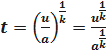 ;
;
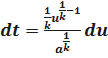 ;
; 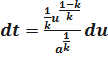 ;
;
если 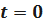 ,то
,то 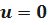 .
.
если 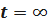 ,то
,то 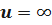 .
.
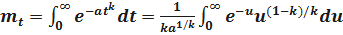 .
.
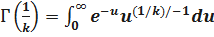 – гамма-функция
– гамма-функция
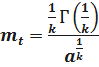
Определим дисперсию времени безотказной работы T.
Имеем
 ;
;
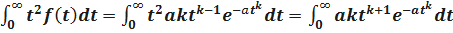 ;
;
Введём новую переменную u вида
 ;
; 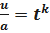 ;
; 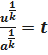 ;
;
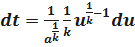 ;
;
если 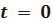 ,то
,то 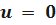 .
.
если 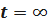 ,то
,то 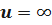 .
.
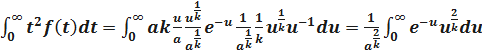 .
.
Известно следующее соотношение для гамма – функции.
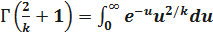 ;
;
Следовательно 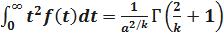 .
.
Тогда
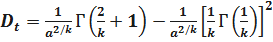 .
.
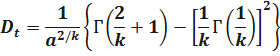
Рассмотрим случай, когда 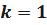 ;
; 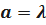 .
.
В этом случае имеем 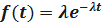 .
.
Т.е. в этом случае имеем экспоненциальный закон надёжности.
Пусть 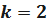 . В этом случае имеем закон Рэлея. Закон Вейбулла лучше описывает время безотказной работы изделия, чем экспоненциальный закон, т.к. в этом случае имеется два параметра: a и k. Пусть
. В этом случае имеем закон Рэлея. Закон Вейбулла лучше описывает время безотказной работы изделия, чем экспоненциальный закон, т.к. в этом случае имеется два параметра: a и k. Пусть 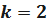 ;
; 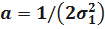 . Тогда имеем
. Тогда имеем 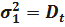 ;
;
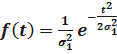 - закон распределения Рэлея.
- закон распределения Рэлея.
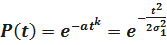 ;
; 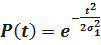 ;
;
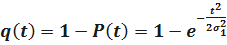 ;
;
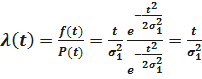 ;
;
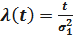 ;
;
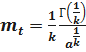 ;
; 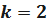 ;
; 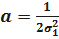 ;
; 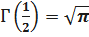 ;
;
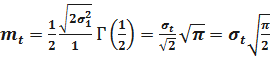 ;
;
| <== предыдущая страница | | | следующая страница ==> |
| Законы распределения отказов и их основные характеристики | | | Виды соединения элементов в систему |
Дата добавления: 2014-08-09; просмотров: 376; Нарушение авторских прав

Мы поможем в написании ваших работ!