
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Метод наименьших квадратов. Пусть по выборке , требуется определить оценки эмпирического уравнения регрессии (8)
Пусть по выборке 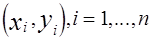 , требуется определить оценки
, требуется определить оценки 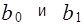 эмпирического уравнения регрессии (8).
эмпирического уравнения регрессии (8).
В этом случае при использовании МНК минимизируется следующая функция:
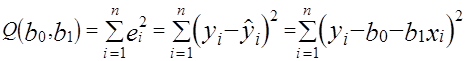 (10)
(10)
Нетрудно заметить, что функция 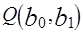 является квадратичной функцией двух параметров
является квадратичной функцией двух параметров 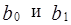 , поскольку
, поскольку 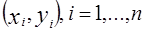 — известные данные наблюдений. Так как функция
— известные данные наблюдений. Так как функция 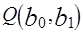 непрерывна, выпукла и ограничена снизу
непрерывна, выпукла и ограничена снизу 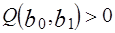 , то она имеет минимум.
, то она имеет минимум.
Необходимым условием существования минимума функции двух переменных (10) является равенство нулю ее частных производных по неизвестным параметрам 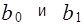 .
.
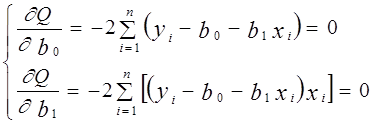 (11)
(11)
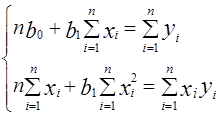 (12)
(12)
Решение данной системы имеет вид:
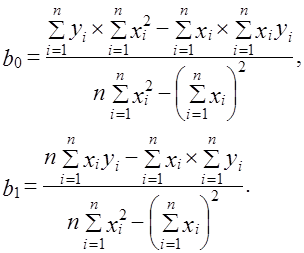 (13)
(13)
Таким образом, по МНК оценки параметров 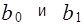 определяются по формулам (13).
определяются по формулам (13).
Проведенные рассуждения позволяют сделать ряд выводов:
1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитывать.
2. Оценки МНК являются точечными оценками теоретических коэффициентов регрессии.
3. Согласно второй формуле соотношения (13), эмпирическая прямая регрессии обязательно проходит через точку 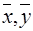 .
.
4. Эмпирическое уравнение регрессии построено таким образом, что сумма отклонений 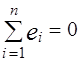 , а также среднее значение отклонения
, а также среднее значение отклонения 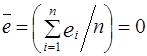 .
.
5. Отклонения 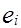 не коррелированы с наблюдаемыми значениями
не коррелированы с наблюдаемыми значениями 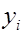 переменной
переменной 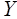 .
.
6. Отклонения 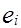 , не коррелированы с наблюдаемыми значениями
, не коррелированы с наблюдаемыми значениями 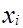 независимой переменной
независимой переменной 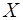 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Тема 2. Парная линейная регрессия | | | Введение. Тема: Предмет и основные задачи ветеринарной экологии |
Дата добавления: 2014-03-11; просмотров: 347; Нарушение авторских прав

Мы поможем в написании ваших работ!