Тема 2. Парная линейная регрессия

Если функция регрессии линейна, то говорят о линейной регрессии. Модель линейной регрессии (линейное уравнение) является наиболее простым видом зависимости между экономическими переменными. Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.

Линейная регрессия (теоретическое линейное уравнение регрессии) представляет собой линейную функцию между условным математическим ожиданием 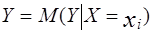зависимой переменной 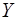и одной объясняющей переменной 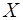(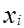— значения независимой переменной в 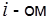наблюдении, ).

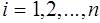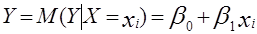(5)

Принципиальной является линейность уравнения по параметрам 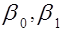. Так как каждое индивидуальное значение 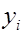отклоняется от соответствующего условного математического ожидания, в соотношение (5) необходимо ввести случайное слагаемое ,

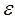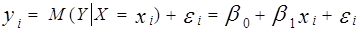(6)

Соотношение (6) называется теоретической линейной регрессионной моделью, 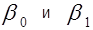— теоретическими параметрами (теоретическими коэффициентами) регрессии, 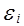— случайным отклонением.

Следовательно, индивидуальные значения 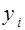представляются в виде суммы двух компонент — систематической 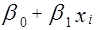и случайной 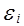. В общем, виде теоретическую линейную регрессионную модель будем представлять в виде

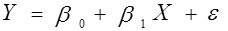(7)

Для определения значений теоретических коэффициентов регрессии необходимо знать и использовать все значения переменных 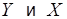генеральной совокупности, что невозможно.

Таким образом, задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным 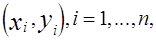для переменных :

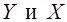а) получить наилучшие оценки неизвестных параметров ;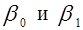

б) проверить статистические гипотезы о параметрах модели;

в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Следовательно, по выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии

(8)

где 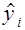— оценка условного математического ожидания 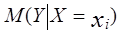; 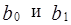— оценки неизвестных параметров 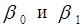, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае

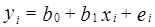, (9)

где отклонение 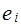— оценка теоретического случайного отклонения .

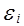В силу несовпадения статистической базы для генеральной совокупности и выборки оценки 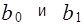практически всегда отличаются от истинных значений коэффициентов 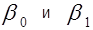, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к определению отличающихся друг от друга оценок.

Задача состоит в том, чтобы по конкретной выборке 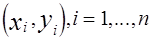найти оценки 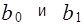неизвестных параметров 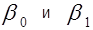так, чтобы построенная линия регрессии являлась бы наилучшей в определенном смысле среди всех других прямых линий. Построенная прямая 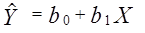должна быть «ближайшей» к точкам наблюдений по их совокупности.

Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется сумма 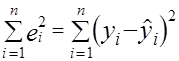. Он получил название метод наименьших квадратов (МНК). Этот метод оценки является наиболее простым с вычислительной точки зрения. Кроме того, оценки коэффициентов регрессии, найденные МНК при определенных предпосылках, обладают рядом оптимальных свойств.

Дата добавления: 2014-03-11; просмотров: 332; Нарушение авторских прав

Мы поможем в написании ваших работ!