Вращение абсолютно твёрдого тела вокруг неподвижной оси

Вращение твердого тела

Вращением твёрдого тела называется такой вид движения, при котором, по крайней мере, одна точка твёрдого тела остаётся неподвижной. Рассмотрим, однако, более простой случай – вращение АТТ вокруг неподвижной оси.

Закрепим две точки АТТ:. Рассмотрим, как будут двигаться все точки твёрдого тела и научимся определять скорости и ускорения этих точек. Ясно, что точки твёрдого тела, лежащие на прямой, проходящей через две закреплённые точки, двигаться не будут: эту прямую называют неподвижной осью вращения. Движение твёрдого тела, при котором по крайней мере две его точки неподвижны, называют вращением АТТ вокруг неподвижной оси.

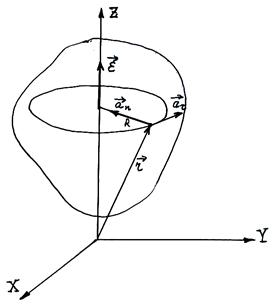
Ясно, что точки не лежащие на оси вращения описывают окружности, центры которых лежат на оси вращения. Плоскости, в которых лежат такие окружности, перпендикулярны оси вращения. Следовательно: нам известны траектории всех точек тела. Это позволяет приступить к нахождению скорости любой точки твёрдого тела.

При естественном способе задания движения точки:

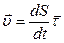(1.32)

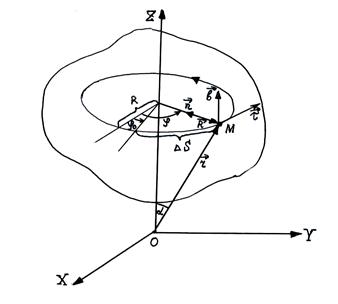Выберем неподвижную систему отсчёта, ось 0Z которой совпадает с осью вращения. Угол между неподвижной плоскостью X0Z, проходящей через ось вращения и плоскостью, жёстко связанной с твёрдым телом и проходящей через ось вращения, обозначим через. В начальный момент времени . Рассмотрим движение точки М по окружности радиуса R.

; ; .

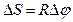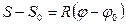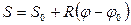Продифференцируем по времени полученное уравнения, учитывая, что величины R, S₀и 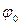являются постоянными:

(1.33)

Подставив (1.33) в (1.32) получим:

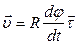(1.34)

Эта формула неудобна, потому что сюда входит единичный вектор 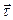, который зависит от положения точки. Мы привыкли положение точки задавать радиус-вектором 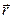. Он должен входить в формулу для скорости. Для этого проведём следующие преобразования:

используя, что 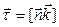, перепишем соотношение (1.34) в виде

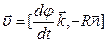(1.35)

Обозначим:

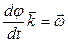– не зависит от выбора рассматриваемой точки М; (1.36)

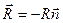– вектор, проведенный из центра окружности к точке М. (1.37)

Ясно, что модуль 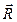равен радиусу окружности.

Подставим (1.36) и (1.37) в (1.35):

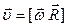(1.38)

Докажем, что 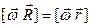(1.39)

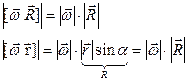
Направления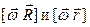совпадают с направлением единичного вектора касания .

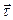Следовательно: тождество (1.39) справедливо. Осуществив замену (1.39) уравнение (1.38) запишем в виде:

– линейная скорость точки М. (1.40)

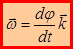– угловая скорость. (1.41)

Угловая скорость – величина одинаковая для всех точек твердого тела.

Линейная скорость любой точки твёрдого тела, вращающегося вокруг неподвижной оси, равна векторному произведению угловой скорости АТТ на радиус-вектор, проведённый из произвольной точки оси вращения, разложим 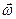по ортам:

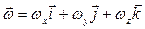. (1.42)

Сравнивая (1.42) и (1.41) получим:

;

модуль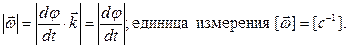

Модуль угловой скорости 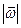связан с частотой вращения 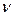абсолютно твердого тела:

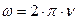
При вращении тела его угловая скорость может изменяться, необходимо уметь определить угловую скорость тела в любой момент времени. Для этого введена величина, которая характеризует изменение угловой скорости с течением времени. Эту величину называют угловым ускорением.

Дадим определение углового ускорения.

Пусть в момент времени t угловая скорость 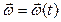. А в момент времени t+∆t угловая скорость равна 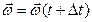. Составим отношение изменения угловой скорости к промежутку времени, в течение которого это изменение происходит, и найдём предел этого отношения при ∆t → 0. В механике этот предел называют угловым ускорением тела и обозначают 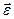поэтому: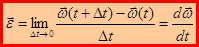. Угловое ускорение – величина одинаковая для всех точек твердого тела. Единицей измерения углового ускорения является .

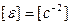Используя (1.40) определим линейное ускорение точки М:

.

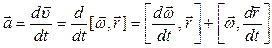Для углового ускорения, его проекции на ось 0Z, модуля углового ускорения справедливы соотношения:

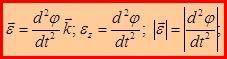
(1.43)

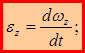
Перепишем выражение для ускорения точки:

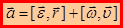(1.44)

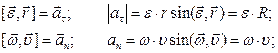
Тангенциальное ускорение любой точки твёрдого тела, вращающегося вокруг неподвижной оси, равно векторному произведению углового ускорения тела на радиус – вектор этой точки, проведённой из произвольной точки оси вращения.

Дата добавления: 2014-03-11; просмотров: 479; Нарушение авторских прав

Мы поможем в написании ваших работ!