Механический принцип относительности

Уравнение, выражающее основной закон динамики 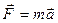отчётливо показывает, что этот закон не может быть справедлив в любой системе отсчёта. Допустим, что система отсчёта XYZ инерциальна. Рассмотрим вторую систему отсчёта X’Y’Z’, движущуюся относительно первой поступательно с постоянной скоростью 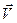=const.

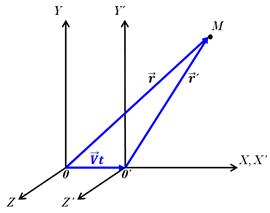Пусть известно движение материальной точки в системе XYZ. Каким будет движение этой же точки в системе координат X’Y’Z’?

Для простоты будем считать оси координат соответственно параллельными.

При t = 0 начала совпадают систем координат совпадают. Скорость 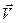направлена в сторону возрастания осей X и X’. Из рисунка видно:

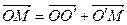или

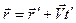(3.1)

Отсюда 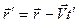. Учитывая, что время в механике Ньютона абсолютно 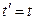, получаем выражения для координат точки М в подвижной системе координат:

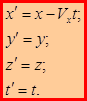– преобразования Галилея, решают поставленную задачу.

Дифференцируем (3.1) по времени:

,

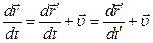или:

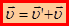– закон сложения скоростей. (3.2)

Дифференцируем (3.2) по времени: .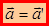

Таким образом, ускорение одно и той же в системах XYZ и X’Y’Z’. Говорят, что ускорение инвариантно относительно преобразования Галилея.

Если 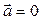, то и 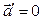. Следовательно, если XYZ – инерциальная система координат, то и X’Y’Z’ – инерциальная система отсчета.

Пусть система XYZ – инерциальная. Но m=m’, 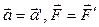(она есть функция инвариантных величин – разности координат и разностей скоростей материальных точек).

Отсюда 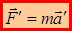. Таким образом: уравнения механики Ньютона инвариантны относительно преобразований Галилея – эта формулировка отражает принцип относительности Галилея или механический принцип относительности.

Однако движения материальной точки могут быть различными – всё зависит от начальных условий.

Дата добавления: 2014-03-11; просмотров: 323; Нарушение авторских прав

Мы поможем в написании ваших работ!