
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
И законы сохранения
Общие теоремы динамики материальной точки
Общие теоремы динамики материальной точки есть логическое следствие основного закона динамики материальных тел: 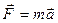 . Общие теоремы позволяют ввести ряд новых физических понятий, что позволяет полнее раскрыть закономерности механического движения.
. Общие теоремы позволяют ввести ряд новых физических понятий, что позволяет полнее раскрыть закономерности механического движения.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ И ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ
Перепишем основной закон динамики материальной точки, используя определение ускорения: 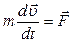 . Т.к. m = const, то:
. Т.к. m = const, то: 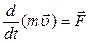 . Вектор
. Вектор  – называют импульсом материальной точки или количеством движения материальной точки.
– называют импульсом материальной точки или количеством движения материальной точки.  – дифференциальная форма теоремы об изменении импульса материальной точки: дифференциал импульса материальной точки равен элементарному импульсу силы, приложенной к ней.
– дифференциальная форма теоремы об изменении импульса материальной точки: дифференциал импульса материальной точки равен элементарному импульсу силы, приложенной к ней.
Интегрируя данное уравнение по промежутку времени ∆t = t2 – t1, получим интегральную формулировку теоремы об изменения импульса материальной точки:
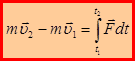
В проекциях на оси координат:
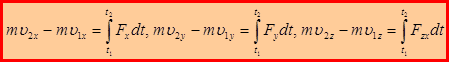
Из уравнения 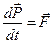 следует, что если
следует, что если 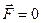 , то
, то 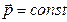 . В случае, когда на материальную точку действует несколько сил:
. В случае, когда на материальную точку действует несколько сил: 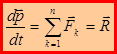 .
.
Если 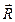 =0, то
=0, то 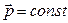 . Закон сохранения импульса материальной точки: если равнодействующая сил, приложенных к материальной точке равна нулю, то импульс материальной точки остаётся постоянным.
. Закон сохранения импульса материальной точки: если равнодействующая сил, приложенных к материальной точке равна нулю, то импульс материальной точки остаётся постоянным.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ
Моментом силы относительно произвольной точки О называют вектор 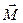 , определяемый формулой
, определяемый формулой
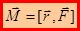 , где
, где 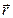 – вектор, проведённый из точки О в точку приложения силы.
– вектор, проведённый из точки О в точку приложения силы.
Модуль момента силы: 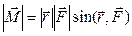
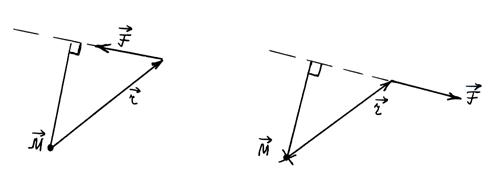 |
Момент силы направлен перпендикулярно плоскости, в которой находятся вектора
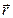 и
и 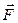 .
.
Здесь плечо силы – длина перпендикуляра, опущенного из начала вектора 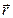 на линию действия силы.
на линию действия силы.
Совместив начало вектора 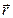 с началом системы координат получим выражение для проекций момента силы:
с началом системы координат получим выражение для проекций момента силы:
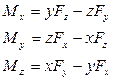
Аналогично моменту силы введём понятие момента импульса материальной точки:

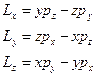
Умножим левую и правую часть уравнения, выражающее теорему об изменении импульса материальной точки 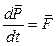 , слева векторно на радиус-вектор точки:
, слева векторно на радиус-вектор точки:
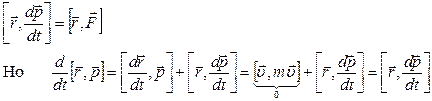
Следовательно:
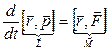
| <== предыдущая страница | | | следующая страница ==> |
| Характеристика сил | | | Работа силы. Мощность |
Дата добавления: 2014-03-11; просмотров: 290; Нарушение авторских прав

Мы поможем в написании ваших работ!