Оператор а трёхфазной системы

Расчёт трёхфазных цепей

Преимущества трёхфазных систем

Широкое распространение трёхфазных систем объясняется главным образом тремя основными причинами:

a) Передача энергии на дальние расстояние трёхфазным током экономически более выгодно, чем переменным током с иным числом фаз

b) Элементы системы – трёхфазный асинхронный двигатель, трёхфазный синхронный генератор и трёхфазный трансформатор – весьма просты в производстве, экономичны и надёжны в работе

c) Система обладает свойством неизменности величины мгновенной мощности за период синусоидального тока, если нагрузка во всех трёх фазах одинаковая

Трёхфазные цепи являются разновидностью цепей синусоидального тока и потому расчёт и исследование процессов в них производится теми же методами и приёмами, которые рассматривались ранее.

Для цепей трёхфазного тока применим так же символический метод расчёта, могут строиться векторные, топографические и круговые диаграммы.

Аналитический расчёт рекомендуется сопровождать построением векторных или топографических диаграмм, что помогает находить ошибки при аналитическом расчёте, если последние возникают.

Условимся комплексное число е_­^j120° ­по модулю равное единице, обозначить через а и называть оператором трёхфазной системы

е_­^j120° ­= а (28)

Тогда

е_­^j240° =(е_­^j120° ­)­_­² = а² (29)

Умножение любого вектора на а означает поворот его без изменения модуля на 120° против часовой стрелки. Умножение вектора на а² поворачивает его на угол 240° против часовой стрелки, или, что то же самое, поворачивает его на 120° по часовой стрелке.

Три вектора 1, а, а² – образуют симметричную трёхфазную систему, а сумма векторов любой симметричной системы равна нулю (рис. 19).

1 + а + а² = 0 (30)

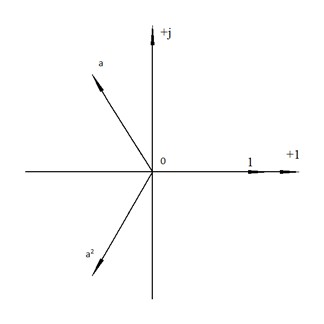
Рис. 19. Симметричная система трёх единичных векторов

С помощью оператора а можно выразить ЭДС Е́_В и Е́_С симметричной трёхфазной системы через ЭДС Е́_А:

Е́_В = а²* Е́_А; Е́_С = а*Е́_А; (30)

Расчёт схемы звезда – звезда с нулевым проводом (рис. 20)

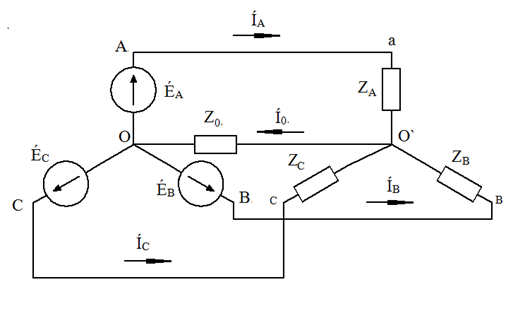
Рис. 20. Схема соединения звезда – звезда с нулевым проводом

Если нулевой провод обладает весьма малым сопротивлением, т.е. Z₀=0, то потенциал точки О` практически равен потенциалу точки О, точки О` и О фактически представляют собой одну точку:

ϕ́₀ = ϕ́₀` (32)

При этом в схеме образуются три обособленных контура, токи в которых даже при неравномерной нагрузке можно определить по простым формулам:

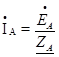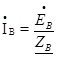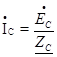; ; ; (33)

При равномерно нагрузке линейные токи Í_A, Í_B, Í_C образуют симметричную систему векторов, т. е. сдвинутых на 120° один относительно другого. Их сумма равна нулю:

Í_A + Í_B + Í_C = 0, (34)

т. е. ток нулевого провода равен нулю.

При неравномерной нагрузке линейные тока могут оказаться под любым углом по отношению друг к другу. Появляется ток нулевого провода Í₀, который можно определить по первому закону Кирхгофа для любого узла:

Í₀ = Í_A + Í_B + Í_C (35)

Если в нулевом проводе есть сопротивлениеZ­₀, то расчёт следует проводить по методу узловых потенциалов. Точка О генератора всегда заземляется по правилам техники безопасности, т. е.

ϕ́₀ = 0 (36)

Составим уравнение для узла О`:

ϕ́_0`(Y_A+Y_B+Y_C+Y₀) = Е́_АY_A+ Е́_ВY_В+ Е́_СY_С,

отсюда получаем

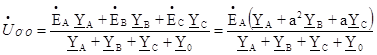(37)

где Y_A, Y_B, Y_C, Y₀ – комплексные проводимости фаз А, В, С и нулевого провода соответственно.

Если нагрузка неравномерная 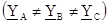, то 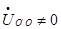и тогда фазные напряжения нагрузок будут:

Ú_{AO`</sub>=É<sub>А</sub> - Ú<sub>O`О}, Ú_{ВO`</sub>=É<sub>В</sub> - Ú<sub>O`О}, Ú_{СO`</sub>=É<sub>С</sub> - Ú<sub>O`О} (38)

А токи в фазах нагрузки будут найдены:

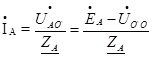; (39)

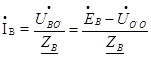; (40)

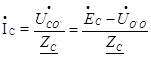; (41)

Линейные токи Í_A, Í_B, Í_C образуют несимметричную систему и появляется ток нулевого провода Í₀, который можно найти по первому закону Кирхгофа:

Í₀ = Í_A + Í_B + Í_C, (42)

или по формуле

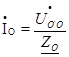(43)

Естественно, по обеим формулам должно получиться одно и то же.

Если нагрузка равномерная 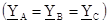, то:

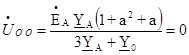(44)

так как 1 + а­² + а = 0

Линейные токи Í_A, Í_B, Í_C образуют симметричную систему:

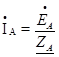; ; ; (45)

Ток нулевого провода будет равен нулю:

Í₀ = Í_A + Í_B + Í_C = 0. (46)

Дата добавления: 2014-02-26; просмотров: 731; Нарушение авторских прав

Мы поможем в написании ваших работ!