
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Примеры. §1.1. Инерциальные системы отсчета
Глава 2. Динамика
Глава 1. Кинематика.
§1.1. Инерциальные системы отсчета. Принцип относительности.
Всякое движение есть изменение состояния физического объекта. Механическим движением называется перемещение тел или частей тела друг относительно друга. Для его описания необходимо выбрать систему отсчета. Она состоит из тела отсчета и способа отсчета времени (неподвижных относительно этого тела «часов»). Система отсчета есть выражение фундаментального свойства природы: движение относительно и происходит в пространстве и во времени. Поскольку пространство и время всегда рассматриваются в конкретной системе отсчета, то пространство и время относительны, как относительно движение.
Преимуществом в физике пользуется инерциальная система отсчета. Она связана со свободным телом. Свободным называется тело, настолько удаленное от всех прочих, что их воздействием на движение данного тела можно пренебречь. Закон природы, отраженный в принципе инерции Галилея (он же является первым законом Ньютона) гласит: в инерциальной системе отсчета свободное тело покоится или движется равномерно и прямолинейно. Следовательно, любая система отсчета, покоящаяся или движущаяся равномерно и прямолинейно относительно инерциальной, также является инерциальной. Другими словами, никакими опытами, проводимыми внутри инерциальной системы отсчета, нельзя определить, покоится она или движется равномерно и прямолинейно, так что понятие абсолютного покоя лишено смысла, и инерциальных систем отсчета бесконечно много. К инерциальным системам отсчета применим еще один универсальный закон природы - принцип относительности. Он гласит: все законы физики имеют одинаковый вид во всех инерциальных системах отсчета. Физические законы выражаются математическими формулами, так что принцип относительности формулируется еще так: физические законы инвариантны относительно перехода от одной инерциальной системы отсчета к другой. Инвариантность означает неизменность вида уравнений при каких-либо преобразованиях, в частности, в любых инерциальных системах отсчета один и тот же закон природы выражает одна и та же формула. Принцип относительности проявляется в совпадении результатов опытов (их воспроизводимости), проведенных разными исследователями в разное время и в разных местах при одинаковых условиях. Следствием этого является накопление знаний и технический прогресс.
Опыт показывает, что инерциальной является система отсчета, образованная Солнцем с неподвижными относительно него часами. Она называется гелиоцентрической. На практике чаще всего движения тел рассматривают относительно земли, и тогда систему отсчета удобно связывать с землей. Такая система называется геоцентрической. Однако эта система неинерциальная, потому что она движется относительно гелиоцентрической системы с ускорением в силу двух причин: Земля движется вокруг Солнца (смена времен года), и Земля вращается вокруг собственной оси (смена времени суток). Центростремительное ускорение Земли при ее вращении вокруг Солнца составляет около 6.10-3 м/с2, центростремительное ускорение при суточном вращении Земли около 3.10-2 м/с2. В задачах, где требуемая точность позволяет пренебречь этими численными значениями по сравнению с численным значением ускорения свободного падения g = 9,8 м/с2, Землю можно считать инерциальной системой отсчета. Доказательством неинерциальности Земли является маятник Фуко. Его плоскость качания, сохраняя неименную ориентацию относительно Солнца, поворачивается относительно Земли за сутки на 3600.
§1.2. Поступательное и вращательное движения
Для теоретического описания физических объектов используют их модели. Две простейшие модели механики - материальная точка и абсолютно твердое тело. Материальной точкой (м.т.) называют тело, размеры которого, форма, внутренняя структура и протекающие в нем процессы не влияют на его движение в данной задаче. Модель абсолютно твердого тела (а.т.т.) считают системой материальных точек, взаимное расположение которых не изменяется. Эта модель учитывает размеры и форму тела, но пренебрегает их изменением при движении, т.е. деформациями.
Движение тела, при котором скорости и, соответственно, ускорения всех его точки одинаковы в любой момент времени, называется поступательным. При вращательном движениитраектории всех точек тела – окружности, их плоскости совпадают или параллельны друг другу, а центры лежат на одной прямой (ее называют ось вращения). Любое движение а.т.т. можно представить как сумму поступательного и вращательного движений.
Кинематика занимается описанием механического движения. Ее задача – указать положение тела в пространстве, а также его скорость и ускорение в любой момент времени. Эти три кинематические характеристики взаимосвязаны, так что знание одной из них как функции времени позволяет найти две остальные.
§1.3. Закон (кинематическое уравнение) движения
Положение тела в пространстве задает закон движения. Он может быть представлен графиком, таблицей, уравнением (его называют кинематическим уравнением движения). Минимальное число параметров (координат), задающих положение тела, называется его числом степеней свободы – i . При движение в пространстве м.т. или при поступательном движении а.т.т. число степеней свободы i =3. Такое движение называют трехмерным. Движение по известной поверхности имеет две степени свободы и называется двухмерным, движение по известной траектории называется одномерным.
Положение материальной точки в пространстве указывает радиус - вектор 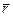 , проведенный из начала отсчета в точку, где находится тело (рис. 1). При движении этот вектор изменяется со временем t, так что закон движения в векторной форме выражает уравнение:
, проведенный из начала отсчета в точку, где находится тело (рис. 1). При движении этот вектор изменяется со временем t, так что закон движения в векторной форме выражает уравнение:
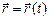 (1.3.1)[1]
(1.3.1)[1]
В декартовой системе координат этот же закон движения в координатной форме выражают три скалярных уравнения:
x=x(t)
y=y(t) (1.3.2)
z=z(t)
Координатная форма есть выражение принципа независимости движения: пространственное движение м.т. можно представить как сумму трех прямолинейных движений вдоль осей координат.
Линия, по которой движется тело, называется траекторией. Закон движения задает уравнение траектории: при движении тела конец радиуса вектора 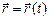 рисует
рисует  траекторию. Закон движения в координатной форме (1.3.2) задает это уравнение в параметрической форме, где параметром является время t . Подчеркнем, что понятие траектории применимо только в классической физике, для квантовых частиц оно теряет смысл. При одномерном движении закон движения превращается в одно скалярное уравнение:
траекторию. Закон движения в координатной форме (1.3.2) задает это уравнение в параметрической форме, где параметром является время t . Подчеркнем, что понятие траектории применимо только в классической физике, для квантовых частиц оно теряет смысл. При одномерном движении закон движения превращается в одно скалярное уравнение:
s = s(t) (1.3.3)
В приведенном уравнении s – координата точки траектории.
Рассмотрим вращательное движение а.т.т. (рис.2). Ось вращения неподвижна, на рисунке скобочки изображают подшипники, в которых ось закреплена. Указаны траектории движения двух точек тела. Радиусы и плоскости окружностей, описываемых этими точками, различны, а вот центральные углы, на которые опираются дуги, описанные разными точками при вращении тела, одинаковы. Вращающееся тело имеет всего одну степень свободы (i =1), и его положение в пространстве задает одна координата j - угол поворота тела относительно некоторого положения, выбранного за начало отсчета. Закон вращательного движения выражает уравнение
j = j(t) (1.3.4)
§1.4. Скорость
Следующая кинематическая характеристика движения – скорость – выражает быстроту изменения 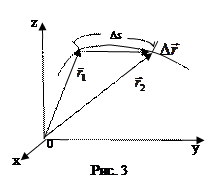 положения тела в пространстве. Изменение положения в пространстве материальной точки характеризуют вектором перемещения:
положения тела в пространстве. Изменение положения в пространстве материальной точки характеризуют вектором перемещения:
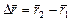 (1.4.1)
(1.4.1)
Путь Ds – это расстояние, пройденное телом по траектории, по определению положительная величина (рис.3). При движении по прямолинейной траектории в одном направлении модуль вектора веремещения и пройденный путь равны друг другу: ½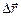 ½= Ds. При движении по криволинейной траектории, а также при изменении направления движения по траектории любой формы½
½= Ds. При движении по криволинейной траектории, а также при изменении направления движения по траектории любой формы½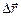 ½< Ds. Вектор средней скорости за промежуток времени Dt = t2 – t1
½< Ds. Вектор средней скорости за промежуток времени Dt = t2 – t1
<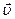 >=
>= 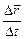
 (1.4.2)
(1.4.2)
Направление вектора средней скорости совпадает с направдением вектора перемещения. Из рис.3 видно, что если рассматриваемый участок пути разделить на два одинаковых, то на каждом из них векторы средних скоростей будут различаться, так что <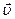 > - довольно грубая характеристика движения. Для получения более точной характеристики надо рассматривать маленькие участки траектории, которым соответствуют маленькие промежутки времени. Предел выражения (1.4.2) при стремлении промежутка времени Dt к нулю дает мгновенную скорость. В математике такую операцию называют нахождением производной, так что по определению вектор мгновенной скорости
> - довольно грубая характеристика движения. Для получения более точной характеристики надо рассматривать маленькие участки траектории, которым соответствуют маленькие промежутки времени. Предел выражения (1.4.2) при стремлении промежутка времени Dt к нулю дает мгновенную скорость. В математике такую операцию называют нахождением производной, так что по определению вектор мгновенной скорости
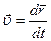 (1.4.3)
(1.4.3)
Направлен 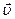 по касательной к траектории, так что ему можно придать вид:
по касательной к траектории, так что ему можно придать вид:
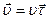 (1.4.4)
(1.4.4)
где υ – модуль скорости, 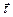 - касательный орт, т.е. единичный вектор, направленный по касательной к траектории.
- касательный орт, т.е. единичный вектор, направленный по касательной к траектории.
На практике зачастую интерес представляет только численное значение скорости. Его легко найти, зная закон движения в скалярной форме (1.3.3):
υ = 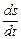 (1.4.5)
(1.4.5)
При движении тела по траектории в положительном направлении скорость будет выражаться положительным числом, и, соответственно, отрицательным при движении в отрицательном направлении.
Когда закон движения задан в координатной форме (1.3.2), то проекции вектора скорости на координатные оси есть первые производные по времени от соответствующих координат:
υx=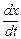 , υ y=
, υ y=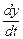 , υ z=
, υ z=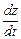 , (1.4.6)
, (1.4.6)
соответственно, модуль вектора скорости:
υ=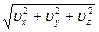 (1.4.7)
(1.4.7)
При вращении тела путь Dj равен угловому перемещению. Его измеряют разностью угловых координат в конечный t2 и начальный t1 моменты времени: Dj = j2 - j1. Малые угловые перемещения (Dj<<2p) можно считать векторами[2], будем их обозначать 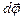 . Этот вектор направлен вдоль оси в соответствии с правилом правого винта, т.е. указывает направление вращения тела, и не имеет фиксированной точки закрепления. Подобные векторы называют аксиальным (осевым) в отличие от полярных векторов, например,
. Этот вектор направлен вдоль оси в соответствии с правилом правого винта, т.е. указывает направление вращения тела, и не имеет фиксированной точки закрепления. Подобные векторы называют аксиальным (осевым) в отличие от полярных векторов, например, 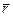 или ∆
или ∆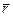 . Быстроту вращения характеризует угловая скорость w. Средняя угловая скорость
. Быстроту вращения характеризует угловая скорость w. Средняя угловая скорость
<w>=Dj /Dt (1.4.8)
Мгновенная угловая скорость
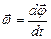 ,
, 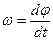 (1.4.9)
(1.4.9)
§1.5. Ускорение
Третья кинематическая характеристика - ускорение - характеризует быстроту изменения скорости. Рассмотрим понятие ускорения для материальной точки. На рис. 4 показаны два положения на траектории 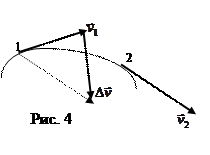 движущейся частицы, соответствующие им скорости
движущейся частицы, соответствующие им скорости 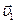 и
и 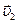 , и приращение скорости
, и приращение скорости 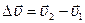 . Вектор среднего ускорения
. Вектор среднего ускорения
<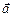 > =
> =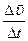 (1.5.1)
(1.5.1)
Мгновенное ускорение:
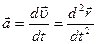 (1.5.2)
(1.5.2)
При прямолинейном движении вектор ускорения совпадает с вектором скорости при ускоренном движении и противоположен ему при замедленном. При движении по криволинейной траектории (см. рис. 4) вектор ускорения направлен под углом к вектору скорости внутрь траектории. Всякий вектор имеет две характеристики – модуль и направление, они могут изменяться независимо друг от друга. При криволинейном движении скорость может изменяться как по величине, так и по направлению, поэтому удобно рассматривать две составляющие вектора ускорения. Используя формулы (1.4.3) и (1.4.4), получаем:
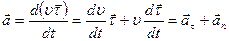 (1.5.3)
(1.5.3)
Вектор ускорения состоит из двух слагаемых – тангенциального 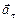 и нормального
и нормального 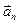 ускорений. Первая составляющая – тангенциальное ускорение характеризует быстроту изменения вектора скорости по величине. При убыстрении движения
ускорений. Первая составляющая – тангенциальное ускорение характеризует быстроту изменения вектора скорости по величине. При убыстрении движения 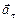 и
и 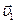 направлены в одну сторону, при замедлении они противоположны. Величина тангенциального ускорения
направлены в одну сторону, при замедлении они противоположны. Величина тангенциального ускорения
at=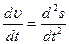 (1.5.4)
(1.5.4)
Вторая составляющая – нормальное ускорение связано с изменением направления скорости. Это хорошо известное из школьного курса физики центростремительное ускорение при равномерном движении тела по окружности. Оно направлено по радиусу к центру окружности и равно:
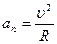 (1.5.5)
(1.5.5)
R – радиус кривизны траектории, т.е. радиус соприкасающейся окружности, дугой которой можно заменить бесконечно малый участок кривой в окрестности данной точки. Задав в этой точке орт нормали 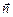 , направленный по радиусу окружности в ее центр, получаем:
, направленный по радиусу окружности в ее центр, получаем:
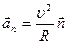 (1.5.6)
(1.5.6)
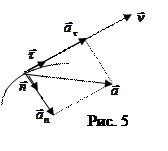 На рис 5 показан небольшой участок траектории, где в данный момент времени находится движущаяся частица. Орты касательный и нормали взаимно перпендикулярны, соответственно, перпендикулярны друг другу тангенциальное и нормальное ускорения, и полное ускорение равно:
На рис 5 показан небольшой участок траектории, где в данный момент времени находится движущаяся частица. Орты касательный и нормали взаимно перпендикулярны, соответственно, перпендикулярны друг другу тангенциальное и нормальное ускорения, и полное ускорение равно:
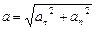 (1.5.7)
(1.5.7)
Если закон движения задан в координатной форме, то модуль ускорения можно вычислить аналогично модулю скорости (см. формулу 1.4.7) так:
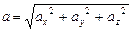 =
= 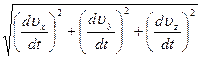 (1.5.8)
(1.5.8)
Проекции вектора ускорения на оси координат соответственно:
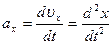 ,
, 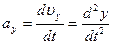 ,
, 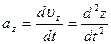 (1.5.9)
(1.5.9)
При вращении тела быстроту изменения его угловой скорости указывает угловое ускорение e. Его среднее значение
<e> = Dw /Dt (1.5.9)
Мгновенное угловое ускорение
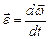 ,
, 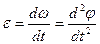 (1.5.10)
(1.5.10)
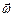 и
и 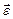 - аксиальные (осевые) векторы. Направление вектора угловой скорости
- аксиальные (осевые) векторы. Направление вектора угловой скорости 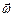 определяет правило правого винта. При ускоренном вращении векторы
определяет правило правого винта. При ускоренном вращении векторы 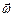 и
и 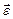 направлены по оси вращения в одну сторону, при замедленном – в противоположные стороны. В СИ угловая координата измеряется в радианах (рад), угловая скорость в рад/с, угловое ускорение в рад/с2.
направлены по оси вращения в одну сторону, при замедленном – в противоположные стороны. В СИ угловая координата измеряется в радианах (рад), угловая скорость в рад/с, угловое ускорение в рад/с2.
§1.6. Равномерное и равнопеременное движения.
В предыдущем параграфе мы рассмотрели, как, зная закон движения, найти скорость и ускорение в любой момент времени. В этом параграфе рассмотрим решение обратной задачи кинематики: найти скорость как функцию времени и получить закон движения, зная зависимость ускорения от времени. Проделаем это на примерах равномерного и равнопеременного движений материальной точки. Убедимся в том, что известные из школы формулы можно легко вывести, а не запоминать.
Равномерным называется движение, когда скорость не изменяется по величине, следовательно, тангенциальное ускорение at =0. Учитывая, что at=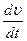 , получаем:
, получаем: 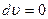 , т.е. υ=
, т.е. υ=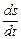 =const. Находим первообразную (интегрируем) и получаем формулу равномерного движения:
=const. Находим первообразную (интегрируем) и получаем формулу равномерного движения:
s=so+υt (1.6.1)
Здесь so –координата тела на траектории в начальный момент времени t=0. Если начало отсчета совместить с начальным положением тела, то so=0, и s = υt.
Равнопеременным называется движение с постоянным ускорением 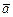 =const. Проинтегрируем формулы (1.5.2), и затем, используя полученный результат, проинтегрируем формулу (1.4.3):
=const. Проинтегрируем формулы (1.5.2), и затем, используя полученный результат, проинтегрируем формулу (1.4.3):
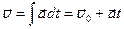 (1.6.2)
(1.6.2)
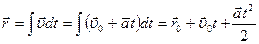 (1.6.3)
(1.6.3)
Аналогичным образом можно получить формулы равномерного и равнопеременного вращения.
§ 1.7. Связь между линейными и угловыми кинематическими характеристиками.
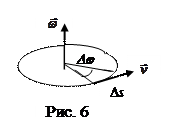 На рис. 6 показана траектория некоторой точки вращающегося тела, отстоящей от оси вращения на расстоянии R, ее линейная скорость
На рис. 6 показана траектория некоторой точки вращающегося тела, отстоящей от оси вращения на расстоянии R, ее линейная скорость 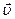 и угловая скорость
и угловая скорость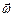 . За промежуток времени Dt тело повернулось на угол Dj, а точка прошла путь Ds. Очевидно, Ds=RDj. Исходя из определений линейной и угловой скоростей (формулы 1.2.9 и 1.2.13) получаем:
. За промежуток времени Dt тело повернулось на угол Dj, а точка прошла путь Ds. Очевидно, Ds=RDj. Исходя из определений линейной и угловой скоростей (формулы 1.2.9 и 1.2.13) получаем:
υ=wR (1.7.1)
Используя формулы (1.2.17), (1.2.18) и (1.4.1), получаем:
at = e R (1.7.2)
an=w 2R (1.7.3)
Обратите внимание, что у точек вращающегося тела нормальное ускорение всегда бывает, а тангенциальное только при неравномерном вращении.
§ 1.8. Краткие итоги главы 1.
Проследим аналогию кинематических характеристик и формул поступательного и вращательного движений.
| Кинематическая характеристика | Вид движения | |
| Поступательное | Вращательное | |
| Координата | S | φ |
| Путь | Δs | Δ φ |
| Скорость средняя | <υ>=Ds/Dt | <υ>=Ds/Dt |
| Скорость мгновенная | 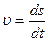
| 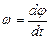
|
| Ускорение среднее | <a>=Dυ/Dt | <e>=Dw /Dt |
| Ускорение мгновенное | at=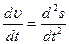
| 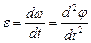
|
| Равномерное движение | ||
| at=0 υ=const s=s0+vt | e=0 w =const j =j0+w t | |
| Равнопеременное движение | ||
| at= const υ=υ0+at t s=s0+υ0 t+at2/2 | e=const e=const j =j0+w0 t+e t2/2 | |
| Связь между линейными и угловыми кинематическими характеристиками | ||
| Путь | s=φR | |
| Скорость | υ=wR | |
| Ускорение | at = e R an=w 2R |
§ 1.9. Примеры
1.



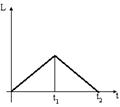
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.
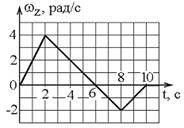
Угловое перемещение (в радианах) за 10 с движения равно …(2, 4, 6, 8)
Решение. Угловое перемещение (путь) на графике зависимости скорости от времени равен площади под графиком. В первые 6 с движения он равен площади треугольника с основанием 6 с и высотой 4 рад/с, а именно 12 рад. В следующие 4 с знак скорости изменился на противоположный, что указывает на изменение направления вращения, и пройденный за это время путь составил 4 рад. Ответ: 8 рад
2.




Частица из состояния покоя начала двигаться по дуге окружности радиуса 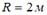 с угловой скоростью, модуль которой изменяется с течением времени по закону
с угловой скоростью, модуль которой изменяется с течением времени по закону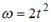 . Отношение нормального ускорения к тангенциальному через 2 секунды равно …(8, 4, 1,2)
. Отношение нормального ускорения к тангенциальному через 2 секунды равно …(8, 4, 1,2)
Решение. Согласно формуле (1.4.8) an=w 2R=2.22.2=16 м/с2. Тангенциальное ускорение вычислим по формулам (1.2.24) и (1.4.2): ε=4t=8 рад/с2, at=16 м/с2. Ответ: 1
3. 



Диск катится равномерно по горизонтальной поверхности со скоростью 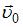 без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении … (1,2,3,4)
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении … (1,2,3,4)
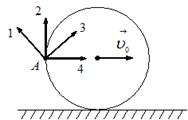 Решение. Точка соприкосновения диска с плоскостью, по которой он катится, является мгновенным центром вращения тела. В рассматриваемый момент времени она неподвижна, а остальные точки тела движутся по окружностям. Их радиусы равны расстояниям от мгновенного центра вращения. Линейная скорость точки, движущейся по окружности, направлена перпендикулярно радиусу (по касательной к траектории). Ответ: 3.
Решение. Точка соприкосновения диска с плоскостью, по которой он катится, является мгновенным центром вращения тела. В рассматриваемый момент времени она неподвижна, а остальные точки тела движутся по окружностям. Их радиусы равны расстояниям от мгновенного центра вращения. Линейная скорость точки, движущейся по окружности, направлена перпендикулярно радиусу (по касательной к траектории). Ответ: 3.
§2.1. Задача динамики. Динамические характеристики
Задача динамики – ответить на вопрос, как будет двигаться тело (найти его закон движения), если известно, каким внешним воздействиям оно подвергается, или, наоборот, найти, каким внешним воздействиям должно подвергаться тело, чтобы выполнялся заданный закон движения. Для теоретического решения такой задачи необходимо следующее: а) задать динамическое состояние тела, б) задать внешнее воздействие, в) составить и решить уравнение динамики. Подтверждением справедливости теории является совпадение ее результатов с опытом.
Опыт показывает, что состояние м.т. определено, если известны ее положение в пространстве и скорость: радиус – вектор 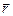 , вектор
, вектор 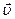 . Нам это кажется очевидным, однако понимание этого появилось только в эпоху Ньютона. Еще Аристотель удивлялся тому, что топор, приставленный к полену, не оставляет на нем даже следа, а топор, ударяющий полено, раскалывает его. Одно и то же положение топора соответствует разным его состояниям, потому что различаются его скорости. Поэтому неудивительно, что разные состояния в начальный момент ведут к разным результатам. Состояние а.т.т. при поступательном движении полностью определяется состоянием любой его материальной точки, т.е.
. Нам это кажется очевидным, однако понимание этого появилось только в эпоху Ньютона. Еще Аристотель удивлялся тому, что топор, приставленный к полену, не оставляет на нем даже следа, а топор, ударяющий полено, раскалывает его. Одно и то же положение топора соответствует разным его состояниям, потому что различаются его скорости. Поэтому неудивительно, что разные состояния в начальный момент ведут к разным результатам. Состояние а.т.т. при поступательном движении полностью определяется состоянием любой его материальной точки, т.е. 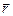 и
и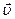 . При вращательном движении состояние тела задают аналогичные кинематические характеристики вращательного движения: угловое положение – φ и вектор угловой скорости -
. При вращательном движении состояние тела задают аналогичные кинематические характеристики вращательного движения: угловое положение – φ и вектор угловой скорости - 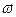 .
.
Закон природы, выраженный принципом инерции Галилея (см.§1.1), утверждает, что состояние свободного тела сохраняется. Его изменение происходит только при взаимодействии с другим телом. Мерой взаимодействия является сила 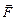 - полярный вектор, имеющей точку приложения, модуль и направление. Вектор силы
- полярный вектор, имеющей точку приложения, модуль и направление. Вектор силы 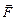 служит мерой внешнего воздействия на материальную точку, а также на тело, движущееся поступательно. При вращательном движении тела результат воздействия зависит не только от приложенной силы, но и от того, где и как она приложена. Мерой воздействия на вращающееся тело является момент сил -
служит мерой внешнего воздействия на материальную точку, а также на тело, движущееся поступательно. При вращательном движении тела результат воздействия зависит не только от приложенной силы, но и от того, где и как она приложена. Мерой воздействия на вращающееся тело является момент сил - 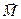 . Вектор момента силы является аксиальным (осевым). При вращении тела относительно неподвижной оси вектор
. Вектор момента силы является аксиальным (осевым). При вращении тела относительно неподвижной оси вектор 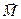 направлен вдоль оси в соответствии с правилом правого винта, и как прочие аксиальные векторы (угловой скорости, углового ускорения), не привязан к конкретной точке оси.
направлен вдоль оси в соответствии с правилом правого винта, и как прочие аксиальные векторы (угловой скорости, углового ускорения), не привязан к конкретной точке оси.
Свойство тела сохранять свою скорость называется инертностью. Мерой инертности м.т. или поступательно движущегося тела является масса m. При вращении тела его инертность зависит не только от массы, но и от ее расстояния от оси вращения: чем дальше масса от оси, тем больше инертность тела, и тем труднее изменить его скорость. Мерой инертности вращающегося тела является момент инерции I. Момент инерции одного и того же тела относительно разных осей вращения может иметь разные значения. В задачах динамики нередко вместо характеристики состояния - скорости, используют другую, более информативную, учитывающую инертность тела. Для материальной точки это импульс 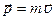 (его устаревшее название – количество движения), для вращающегося тела – момент импульса
(его устаревшее название – количество движения), для вращающегося тела – момент импульса 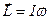
Уравнение динамики, решение которого позволяет найти состояние тела в любой момент времени, основано на трех хорошо известных из школьного курса физики законах динамики Ньютона. Первый закон Ньютона констатирует, что само тело не может изменить свою скорость. Второй закон Ньютона указывает связь между изменением скорости тела и оказываемым на него внешним воздействием. Третий закон Ньютона констатирует, что действие одного тела на другое носит характер взаимодействия, и сила действия равна силе противодействия.
§ 2.2. Виды сил.
Физика насчитывает четыре вида фундаментальных взаимодействий. Два из них – гравитационное и электромагнитное имеют бесконечный радиус действия и проявляют себя как в макро-, так и в микромире. Еще два – сильное (ядерное) и слабое (отвечает за радиоактивный распад) вследствие малости радиуса действия проявляют себя только в микромире, «спрятавшись» внутри ядра атома, и никак себя не проявляет в макромире. Все механические взаимодействия сводятся к трем видам: силе гравитационной (тяжести), силе упругой и силе трения. Силы упругая и трения имеют электромагнитную природу: все тела состоят из атомов, в состав которых входят электрически заряженные частицы.
Гравитационное взаимодействие выражает закон всемирного тяготения:
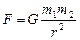 (2.3.1)
(2.3.1)
G – гравитационная постоянная, она введена для согласования единиц измерения величин в обеих частях формулы, в СИ G = 6,67.10-11 Н.м2/кг2 = 6,67.10-11 м3/(кг.с2), т1и т2 – массы материальных точек, r – расстояние между ними. Закон в форме (2.3.1) применим также для вычисления сил тяготения между материальной точкой и телом шарообразной формы, или двух тел шарообразной формы. В этом случае r – расстояние от м.т. до центра шара, соответственно, между центрами шаров. Сила тяготения направлена вдоль r. Масса, фигурирующая в законе всемирного тяготения, называется массой гравитационной или тяготеющей в отличие от массы инертной, измеряющей способность тела сопротивляться изменению состояния под воздействием другого тела. Экспериментально установлено, что эти массы равны друг другу (Р. Этвеш, 1894 г.). Этот опытный факт получил название принципа эквивалентности и лежит в основе общей теории относительности Эйнштейна (теории тяготения). Из принципа эквивалентности, в частности, следует, что сила тяготения со стороны одного тела сообщает всем другим телам одинаковое ускорение независимо от их масс. Например, все тела притягиваются к земле, действующая на них сила тяготения называется силой тяжести, определим ее, используя формулу (2.3.1): 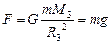 . Здесь
. Здесь 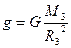 – ускорение свободного падения, M3 и R3 соответственно масса земли и ее радиус. Форма Земли отличается от шара, к тому же плотность вещества неодинакова в разных местах ее объема, но влияние этих параметров столь незначительно, что им можно пренебречь, так что во всех точках поверхности Земли g »9,8 м/с2. Сила тяжести на поверхности земли выражается формулой:
– ускорение свободного падения, M3 и R3 соответственно масса земли и ее радиус. Форма Земли отличается от шара, к тому же плотность вещества неодинакова в разных местах ее объема, но влияние этих параметров столь незначительно, что им можно пренебречь, так что во всех точках поверхности Земли g »9,8 м/с2. Сила тяжести на поверхности земли выражается формулой:
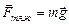 (2.3.2)
(2.3.2)
Из рассмотренного понятно, что на разных планетах сила тяжести и сообщаемое ей ускорение свободного падения различны. Например, сила тяжести на Луне почти в 6 раз меньше, чем на Земле, а по мере удаления космического путешественника от поверхности Земли действующая на него сила тяжести уменьшается.
Сила тяжести является причиной того, что отсутствие опоры (подвеса) вызывает падение тела. Сила, действующая со стороны опоры (подвеса), называется реакцией опоры и направлена всегда перпендикулярно поверхности опоры к телу, т.е. от опоры. Понятно, почему вертикальная поверхность не может служить опорой. Весом тела называется сила, с которой тело давит на опору или тянет подвес, удерживающий его от падения на землю. В соответствии с третьим законом Ньютона вес и реакция опоры (сила действия и сила противодействия) равны друг другу. Понятие невесомости означает отсутствие этих сил, в частности, стоит нам подпрыгнуть, чтобы оторваться от опоры, как мы попадаем в состояние невесомости. В течение всего времени движения, пока мы вновь не приземлимся на опору, сила тяжести не перестает действовать, замедляя движение вверх и ускоряя движение вниз, а вот вес отсутствует. Космонавты в космическом корабле, движущемся с выключенными двигателями, также находятся в состоянии невесомости. Зато при разгоне корабля они испытывают перегрузки, когда вес значительно превышает силу тяжести: реакция опоры должна не только компенсировать силу тяжести, прижимающую космонавта к сиденью, но и сообщить ускорение, направленное от земли. Впрочем, с подобными перегрузками встречаются не только космонавты.
Сила упругости возникает в упруго деформированном теле и противодействует внешней 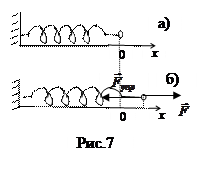 деформирующей силе. Деформации, т.е. изменение расстояний между точками тела в результате внешнего воздействия, называются упругими, если они исчезают после снятия воздействия. Упругими, как правило, бывают только малые деформации. Примером служит упругая деформация сжатой или растянутой пружины. На рис.7 а) показана недеформированная пружина, на рис.7 б) эта же пружина растянута внешней силой
деформирующей силе. Деформации, т.е. изменение расстояний между точками тела в результате внешнего воздействия, называются упругими, если они исчезают после снятия воздействия. Упругими, как правило, бывают только малые деформации. Примером служит упругая деформация сжатой или растянутой пружины. На рис.7 а) показана недеформированная пружина, на рис.7 б) эта же пружина растянута внешней силой 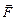 на величину x, в результате в пружине возникает
на величину x, в результате в пружине возникает 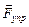 . Величину упругой силы выражает закон Гука:
. Величину упругой силы выражает закон Гука:
F= - kx (2.3.3)
k – коэффициент упругости (жесткость), постоянная для данного тела величина, в СИ измеряется в ньютонах на метр (Н/м). Знак минус указывает на противоположность направлений упругой силы и деформации.
Сила трения препятствует движению тела. Различают трение сухое и трение жидкое.
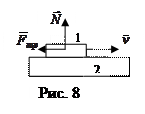 Сила сухого трения возникает между твердыми телами, контактирующими друг с другом вдоль некоторой поверхности, и вызвана тем, что шероховатости поверхности одного тела, цепляясь за шероховатости поверхности другого тела, препятствуют их скольжению друг относительно друга. Рис. 8 иллюстрирует рассматриваемую ситуацию: тело 1 движется со скоростью
Сила сухого трения возникает между твердыми телами, контактирующими друг с другом вдоль некоторой поверхности, и вызвана тем, что шероховатости поверхности одного тела, цепляясь за шероховатости поверхности другого тела, препятствуют их скольжению друг относительно друга. Рис. 8 иллюстрирует рассматриваемую ситуацию: тело 1 движется со скоростью 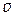 по поверхности тела 2. Опыт показывает, что сила трения скольжения Fтр пропорциональна реакции опоры N и направлена в сторону, противоположную скорости:
по поверхности тела 2. Опыт показывает, что сила трения скольжения Fтр пропорциональна реакции опоры N и направлена в сторону, противоположную скорости:
Fтр = mN (2.3.4)
m - коэффициент трения, безразмерная величина. Его значение зависит от мате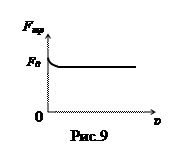 риалов трущихся поверхностей, качества их обработки, загрязненности и обычно считается приблизительно постоянным для двух конкретных тел. В действительности, при стремлении скорости к нулю, отмечается некоторое возрастание силы трения до значения F0.На рис. 9 приведен график модуля силы трения скольжения от величины скорости для движения, изображенного на рис.8.
риалов трущихся поверхностей, качества их обработки, загрязненности и обычно считается приблизительно постоянным для двух конкретных тел. В действительности, при стремлении скорости к нулю, отмечается некоторое возрастание силы трения до значения F0.На рис. 9 приведен график модуля силы трения скольжения от величины скорости для движения, изображенного на рис.8.
Чтобы покоящееся тело 1 пришло в движение, к нему надо приложить силу, чуть превышающую F0. Если внешняя сдвигающая сила F< F0 , то тело 1 останется неподвижным. Это значит, что внешняя сила не в состоянии преодолеть трение, и она уравновешивается силой трения покоя Fпок. Из законов Ньютона следует, что сила трения покоя численно равна и противоположно направлена F. Из сказанного ясно, что 0£ Fпок.£ F0. Для максимальной силы трения покоя иногда пользуются коэффициентом трения покоя m0 в формуле:
F0=m0N (2.3.5)
Отметим, что формула (2.3.5) и m0 имеют смысл только применительно к максимальной силе трения покоя.
Трение жидкое или вязкое возникает при движении слоев жидкости или газа друг относительно друга. Оно встречается при движении твердого тела в жидкости или газе, а также при наличии жидкой (вязкой) смазки между трущимися поверхностями твердых тел. Особенностью жидкого трения является отсутствие трения покоя. Вам, вероятно, приходилось наблюдать, что тяжелое бревно в воде даже ребенок перемещает без труда, тогда как это же бревно, лежащее на суше, не всегда может сдвинуть даже сильный мужчина. Еще отличительной особенностью вязкого трения является возрастание силы трения с увеличением скорости, причем, для небольших скоростей эта зависимость линейная, а при больших скоростях она становится квадратичной. С силой вязкого трения мы встречаемся, плавая и ныряя в воде, а также в ветреную погоду.
Отметим, что действие на тело нескольких сил можно заменить одной. Она называется равнодействующей и равна векторной сумме всех действующих на тело сил:
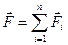 (2.3.6)
(2.3.6)
Формула (2.3.6) есть выражение принципа суперпозиции, т.е. принципа независимого сложения. Этот же принцип позволяет одну силу представить в виде суммы ее проекций, например: 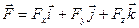
§2.4. Момент инерции.
Момент инерции тела при вращательном движении является аналогом массы при его поступательном движении, а именно, служит мерой инертности тела, т.е. его способности сопротивляться изменению скорости. Из собственного опыта нам известно, что чем дальше вращающаяся масса от оси вращения, тем труднее ускорить или замедлить ее вращение. Момент инерции, как и масса, скалярная величина. Масса (и момент инерции) тела равна сумме масс (моментов инерции) всех его частей. По определению момент инерции тела, являющегося системой материальных точек, выражает формула:
I =Smiri2 (2.4.1)
Здесь mi - масса точки тела с номером i, ri – ее расстояние от оси вращения; суммирование ведется по всем точкам тела. Единица измерения момента инерции в СИ обозначается кг.м2. Инертность тела при вращении зависит от распределения его массы относительно оси вращения, так что одно и то же тело относительно разных осей вращения имеет разные моменты инерции. Для сплошного однородного тела, рассматриваемого как совокупность м.т., с точки зрения математики удобно суммирование свести к интегрированию. Пусть dm – масса физически малого элемента объема dV [3], находящегося на расстоянии r от оси вращения, плотность вещества тела - r (кг/м3), тогда dm=r dV, и момент инерции этого элемента массы dI = r2dm = r2r dV . Формула для вычисления момента инерции сплошного тела примет вид:
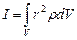 (2.4.2)
(2.4.2)
Интегрирование проводят по всему объему тела, это обозначено ниже знака интеграла.
Приведем формулы моментов инерции некоторых тел, часто встречающихся в практике.
а) Обруч или тонкостенный цилиндр массой m и радиусом R , вращающийся относительно своей оси симметрии.
I0 =Smiri2 = R2Smi = m R2 (2.4.3)
б) Диск или сплошной цилиндр массой m и радиусом R , вращающийся относительно своей оси симметрии.
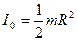 (2.4. 4)
(2.4. 4)
Попробуйте вывести формулу (2.3.4): для этого диск представьте составленным из тонких колец, вставленных друг в друга. Радиусы этих колец плавно изменяются от 0 до R.
в) Шар, вращающийся относительно своей оси (эту формулу нетрудно получить интегрированием, перейдя в сферическую систему координат):
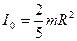 (2.4.5)
(2.4.5)
г) Стержень длиной l, вращающийся относительно перпендикулярной к нему оси, проходящей через его середину (получите эту формулу самостоятельно):
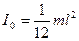 (2.4.6)
(2.4.6)
д) Теорема Штейнера позволяет найти момент инерции тела относительно любой оси, если известен момент инерции относительно параллельной оси, проходящей через центр инерции тела:
I=I0+mb2 (2.4.7)
Здесь I – момент инерции тела относительно рассматриваемой оси, I0 - момент инерции этого же тела относительно оси, проходящей через центр инерции и параллельной рассматриваемой, b – расстояние между этими осями. Обратите внимание, что наименьший момент инерции тела относительно любых параллельных осей в случае, когда ось проходит через цент инерции. Самостоятельно получите формулу для момента инерции стержня, если ось вращения проходит через его коней и перпендикулярна стержню.
§2.5. Момент силы.
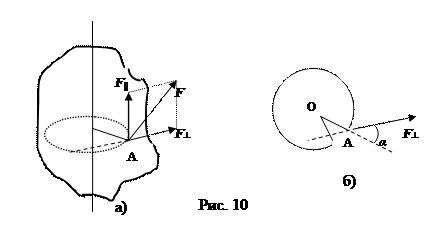 Тело (рис.10) может вращаться вокруг неподвижной оси, изображенной вертикальной линией. В точке А к телу приложена сила
Тело (рис.10) может вращаться вокруг неподвижной оси, изображенной вертикальной линией. В точке А к телу приложена сила 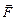 . При его вращении точка А описывает окружность радиусом r. Разложим силу на две составляющие: одна параллельна оси вращения -F||,[4] а другая лежит в плоскости, перпендикулярной оси вращения - F┴. Очевидно, что F|| не может вращать тело. Составляющая F┴ лежит в плоскости траектории, описываемой точкой А (рис. 10-б), и образует угол a с направлением радиуса окружности. Понятно, что если a=0, т.е. линия действия F┴ пересекает ось вращения, то такая сила не вызывает вращения тела. Итак, воздействие на вращающееся тело определяется не только силой, но и тем, где и как она приложена. Эта количественная характеристика воздействия называется моментом силы
. При его вращении точка А описывает окружность радиусом r. Разложим силу на две составляющие: одна параллельна оси вращения -F||,[4] а другая лежит в плоскости, перпендикулярной оси вращения - F┴. Очевидно, что F|| не может вращать тело. Составляющая F┴ лежит в плоскости траектории, описываемой точкой А (рис. 10-б), и образует угол a с направлением радиуса окружности. Понятно, что если a=0, т.е. линия действия F┴ пересекает ось вращения, то такая сила не вызывает вращения тела. Итак, воздействие на вращающееся тело определяется не только силой, но и тем, где и как она приложена. Эта количественная характеристика воздействия называется моментом силы 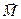 . По определению момент силы относительно оси вычисляют так:
. По определению момент силы относительно оси вычисляют так:
M = F^ d (2.5.1)
d – длина перпендикуляра, опущенного из оси вращения (точка О) на линию действия силы F^, называется плечом силы. На рис.10 б) этот перпендикуляр нарисован, но не обозначен, его длина d=rsinα, где r –расстояние ОА. Единица измерения момента силы в СИ называется ньютон-метр и обозначается Н.м. Вектор момента силы относительно оси 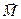 направлен вдоль оси вращения в соответствии с правилом правого винта, на рис. 10 а) вверх по оси.
направлен вдоль оси вращения в соответствии с правилом правого винта, на рис. 10 а) вверх по оси.
§2.6. Уравнение динамики
Общее понятие уравнения динамики мы рассмотрели в §2.1. Оно устанавливает связь между внешним воздействием на тело и изменением состояния тела. Иногда уравнение движения называют основным законом динамики. Обсудим конкретный вид уравнения динамики для двух моделей: м.т. и а.т.т.
Для материальной точки или для поступательно движущегося тела уравнением движения является второй закон Ньютона:
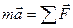 (2.6.1)
(2.6.1)
Это дифференциальное уравнение второго порядка, так как 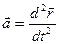 . Если известны все действующие на тело силы
. Если известны все действующие на тело силы 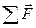 , а также начальное состояние тела, а именно начальная скорость
, а также начальное состояние тела, а именно начальная скорость 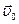 и начальное положение
и начальное положение 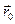 , то решение уравнения (2.6.1) определяет состояние тела в любой момент времени:
, то решение уравнения (2.6.1) определяет состояние тела в любой момент времени:
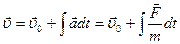 ;
; 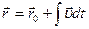 .
.
Отметим, что эту задачу для равнопеременного движения, когда на тело действуют постоянные силы, мы уже решили в §1.6 (смотрите формулы 1.6.2 и 1.6.3)
Уравнению динамики можно придать другой вид, используя понятие импульса 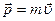 :
:
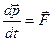 (2.6.2)
(2.6.2)
Здесь 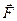 - равнодействующая всех сил (см. формулу 2.3.6). В частности, для прямолинейного движения под действием постоянной силы это уравнение дает формулу:
- равнодействующая всех сил (см. формулу 2.3.6). В частности, для прямолинейного движения под действием постоянной силы это уравнение дает формулу:
∆p=mυ2-mυ1=F∆t (2.6.3)
Напомним, что F∆t – называют импульсом силы.
При вращении твердого тела уравнение движения связывает между собой соответствующие характеристики вращательного движения:
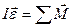 (2.6.4)
(2.6.4)
или в другой форме:
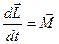 (2.6.5)
(2.6.5)
Здесь 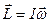 - момент импульса тела,
- момент импульса тела, 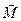 - равнодействующая моментов всех сил, действующих на тело.
- равнодействующая моментов всех сил, действующих на тело.
§2.7. Итоги главы 2. Примеры
Проследим аналогию динамических характеристик и формул поступательного и вращательного движений.
| Характеристика, формула | Вид движения | |
| Поступательное | Вращательное | |
| Состояние | 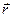 , ,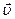 или или 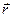 , ,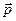
| φ,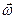 или φ, или φ,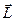
|
| Мера инертности | т – масса, кг | I - момент инерции, кг.,м2
При вращении вокруг оси симметрии момент инерции:
а) обруч, тонкостенный цилиндр: I0 = m R2-
б) диск, сплошной цилиндр:
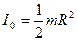 в) шар:
в) шар: 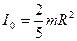
|
| Мера воздействия | 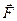 - сила, Н - сила, Н Fтяж= mg - сила тяжести
Fупр = - kx – сила упругости
F=µN – сила трения
Fтяж= mg - сила тяжести
Fупр = - kx – сила упругости
F=µN – сила трения
| 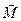 - момент силы, Н.м
M = F^ d –момент силы относительно оси,
F^ - проекция силы на перпендикулярную оси вращения плоскость,
d – ее плечо - момент силы, Н.м
M = F^ d –момент силы относительно оси,
F^ - проекция силы на перпендикулярную оси вращения плоскость,
d – ее плечо
|
| Уравнение движения | 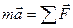 или или
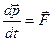 ,
где ,
где 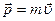 - импульс - импульс
| 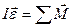 или или
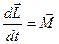 ,
где ,
где 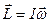 - момент импульса тела - момент импульса тела
|
1.




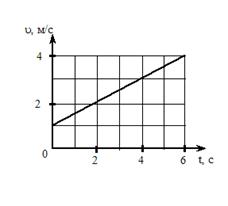
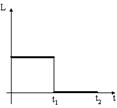
Под действием постоянной силы в 5Н скорость тела изменялась с течением времени, как показано на графике:
Масса тела (в кг) равна … (10)
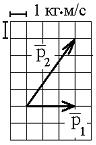
2. Теннисный мяч летел с импульсом 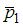 в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью
в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 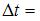 0,1 с. Изменившийся импульс мяча стал равным
0,1 с. Изменившийся импульс мяча стал равным 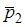 (масштаб указан на рисунке):
(масштаб указан на рисунке):
Средняя сила удара равна … (40 Н)
3. Рассматриваются три тела: диск, тонкостенная труба и кольцо; причем массы m и радиусы R их оснований одинаковы.
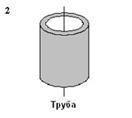
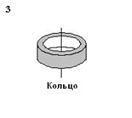
Для моментов инерции рассматриваемых тел относительно указанных осей верным является соотношение …1) I1 < I2 = I3; 2) I1 < I2 < I3; 3) I1= I3< I2; 4) I3< I1< I2
4.Диск вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. К ободу диска приложена сила 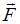 , направленная по касательной.
, направленная по касательной.
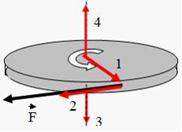
Правильно изображает направление момента силы 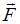 вектор …(3)
вектор …(3)
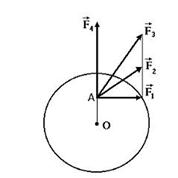 5. Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил (
5. Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. В точке А прикладывают одну из сил (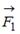 ,
, 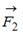 ,
, 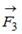 или
или 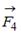 ), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение … (1)
), лежащих в плоскости диска. Верным для моментов этих сил относительно рассматриваемой оси является соотношение … (1)
1) М1=М2=М3, М4=0 2) М1>М2>М3>М4
3) М1<М2<М3<М4 4) М1>М2>М3, М4=0
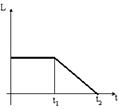
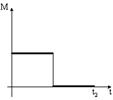 6.Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке:
6.Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке:
Правильно отражает зависимость момента импульса диска от времени график …(1)
1 2
[1] Номер формулы состоит из трех частей: первые две – номер параграфа, третья – порядковый номер формулы в этом параграфе. Номер параграфа содержит два числа: первое – номер главы, второе – порядковый номер параграфа главы.
[2] Только для таких малых углов можно применять векторные операции, например, векторное сложение по правилу параллелограмма. Для больших углов это правило не действует.
[3] В пределах этого объема еще не проявляется дискретность атомного строения вещества, но он достаточно мал, чтобы можно было считать, что свойства вещества одинаковые во всех его точках.
[4] В данном случае вектор обозначен не стрелкой над буквой, а жирным шрифтом. Модуль вектора, как и ранее, обозначен буквой не жирным шрифтом.
| <== предыдущая страница | | | следующая страница ==> |
| В В Е Д Е Н И Е В К У Р С Ф И З И К И | | |
Дата добавления: 2014-03-11; просмотров: 1132; Нарушение авторских прав

Мы поможем в написании ваших работ!