ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ РЕАКЦИИ

В общем случае скорость химической реакции с повышением температуры увеличивается. Опыт показывает, что при повышении температуры на 10°С скорость реакции возрастает в 2—4 раза. Дляхарактеристики зависимости скорости химической реакции от температуры был введен температурный коэффициент скорости реакции g.Этот коэффициент является отношением константы скорости химической реакции при температуре Т +10° к константе скорости при температуре Т, т. е.

g = .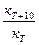

В среднем этот коэффициент равен трем. Следовательно, при изменении температуры на 100°С скорость реакции изменяется в 3¹⁰ = 59049 раз. Пользуясь температурным коэффициентом скорости реакции, можно рассчитывать константы скоростей при различных температурах.

Прологарифмировав выражение , получим

lgk_T+10 – lgk_T = lgg.

Обозначив lgk_T+10 - lgk_T через Dlgk и разделив обе части этого уравнения на DT = 10, получим

= .

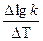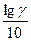Если считать, что в пределах 10° температурный коэффициент остается постоянным, выражение можно записать так:

= .

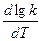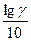Проинтегрировав выражение, получим

lg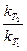 = 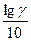(T₂-T₁).

Приведенная выше оценка зависимости скорости химической реакции от температуры носит весьма приближенный характер и имеет малую практическую ценность. Более обоснованную зависимость константы скорости химической реакции от температуры можно получить с помощью уравнения изохоры или изобары химической реакции. Без индексов, характеризующих условия протекания процесса, уравнения изохоры и изобары запишутся одинаково:

= ,

где К = 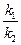— константа химического равновесия; k₁и k₂ — константы скоростей прямой и обратной реакции; DH — теплота химической реакции; R — универсальная газовая постоянная; Т — абсолютная температура.

Подставив вместо константы равновесия отношение констант скоростей, получим

= = .

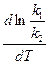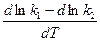Запишем тепловой эффект как разность двух величин:

DH = E₁ – E₂.

Тогда выражение можно переписать так:

- = - .

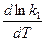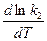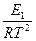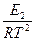С точностью до постоянной величины В можно считать, что слагаемые правой и левой части попарно равны друг другу, т. е.,

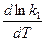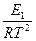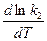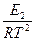= + B;

= + B.

Опыт показал, что B = 0. Поэтому, отбрасывая индексы, в общем виде уравнения можно записать следующим образом:

= .

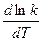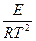Это уравнение, получившее название уравнения Аррениуса,характеризует зависимость константы скорости химической реакции kот температуры Т. Величина Еимеет размерность энергии и носит название энергии активации. Энергию активации можно определить как тот избыток энергии по сравнению со средней энергией молекул при данной температуре, которой должны обладать молекулы, чтобы они могли вступить в химическую реакцию.

Уравнение легко проинтегрировать. Считая, что Е— величина постоянная, получим

lnk = -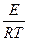 + lnC,

где In С — константа интегрирования.

Если построить зависимость в координатах Ink—l/T, получим прямую линию

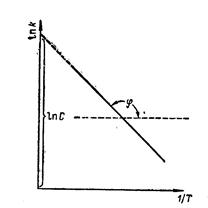
Отрезок, который отсекает эта прямая на оси ординат при 1/Т = 0, равен

In С, а тангенс угла j наклона прямой

tgj = -.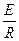

Отсюда можно определить величину энергии активации химической реакции.

Потенциируя выражение, получим

k = Ce ^- .

Из этого уравнения видно, что константами, характеризующими реакцию, являются предэкспоненциальный множитель Си энергия активации Е. Чем больше значение Е, тем меньше (при данном С) скорость химической реакции.

Если выражение проинтегрировать в пределах от T₁ до Т₂, то получим

ln = ,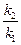

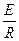
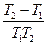где k₂ — константа скорости химической реакции при температуре T₂;k₁— то же при температуре T₁

Таким образом, зная величину k₁при какой-либо температуре T₁, можно вычислить k₂при температуре T₂.

Связь энергии активации с тепловым эффектом реакции можно проиллюстрировать с помощью представления об энергетическом барьере.Химическую реакцию можно представить как переход системы из энергетического состояния I в энергетическое состояние II, сопровождающийся теплотой DH.

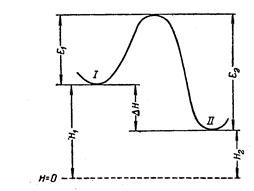
Из рисунка видно, что переход из состояния I в состояние II возможен при затрате энергии Е₁; обратный переход возможен при затрате энергии Е₂. При осуществлении реакции в прямом направлении выделяется количество энергии

-DH = Е₂ - Е₁.

Величина Q_Pравна (по закону Гесса) разности энтальпий исходных и конечных продуктов реакции

-DH = H₁ - H₂ ,

отсчитываемых от некоторого исходного значения, принятого за нулевое

(H = 0).

Дата добавления: 2014-03-11; просмотров: 623; Нарушение авторских прав

Мы поможем в написании ваших работ!