Вопрос 6. Правило сложения дисперсий

Вариация признаков, как правило, обусловлена влиянием различных факторов. Если совокупность разбита на группы по факторному признаку, то это окажет определенное влияние на значение вариации признака в группах. Выявить долю вариации, определяемую теми или иными факторами, можно, разделив всю совокупность на группы по фактору, влияние которого исследуется. В этом случае выделяют три вида дисперсии:

а) общая — измеряет вариацию результативного признака в целом по совокупности под влиянием всех факторов. Количественно вычисляется с помощью формулы взвешенной дисперсий.

б) межгрупповая— характеризует вариацию результативного признака за счет фактора, положенного в основу группировки. и рассчитывается по формуле:

,

где 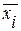- среднее значение признака в i - той группе

f_i – число значений признака в i - той группе

в) внутригрупповая (частная) — измеряет вариацию результативного признака за счет других факторов, не учтенных в группировке:

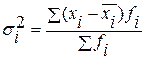
Для всех групп в целом рассчитывается средняя из внутригрупповых дисперсий по формуле:

Между указанными видами дисперсий существует соотношение, которое называют правилом сложения дисперсий - общая дисперсия равна сумме средней из частных дисперсий и межгрупповой:

С помощью правила сложения дисперсий можно оценить удельный вес факторов, лежащих в основе группировки, во всей совокупности факторов, воздействующих на результативный признак. Для этого применяется коэффициент детерминации:

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением:

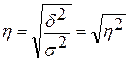
Эмпирическое корреляционное отношение показывает какую часть общей колеблемости результативного признака определяет изучаемый фактор, т.е. характеризует влияние группировочного признака на результативный признак. Это показатель принимает значение от 0 до 1. Если связь отсутствует, то η = 0, В этом случае дисперсия групповых средних равна нулю (δ² = 0), т.е.е все групповые средние равны между собой и межгрупповой вариации нет. Это означает, группировочный признак не влияет на вариацию исследуемого признака. Если связь функциональная, то η = 1, В этом случае дисперсия групповых средних равна общей дисперсии (δ² =σ²), т.е. не будет внутригрупповой дисперсии. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака, а влияние прочих факторных признаков равно 0. Промежуточные значения η оцениваются по степени их близости к предельным.

Дата добавления: 2014-03-11; просмотров: 809; Нарушение авторских прав

Мы поможем в написании ваших работ!