Вопрос 1. Методы анализа основной тенденции развития в рядах динамики

ТЕМА № 6.2. МЕТОДЫ АНАЛИЗА ОСНОВНОЙ ТЕНДЕНЦИИ (ТРЕНДА) В РЯДАХ ДИНАМИКИ

(2 часа)

1. Методы анализа основной тенденции развития в рядах динамики

2. Методы изучения сезонных колебаний

При анализе рядов динамики важно выявить общую тенденцию развития (тренд) социально-экономического явления или процесса, т.е. установить в каком направлении (рост, спад) и в какой зависимости (линейной или нелинейной) оно изменяется. Эта задача в статистике называется выравниванием рядов динамики.

Наиболее простым способом выравнивания рядов является укрупнение интервалов. Суть этого способа заключается в том, что первоначальный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени, например, дневные интервалы заменяются на пятидневные или десятидневные, а месячные интервалы – квартальными и т.п.

Частным случаем данного способа является вычисление средних уровней для укрупненных интервалов.

Одним из распространенных методов выравнивания рядов динамики является их сглаживание посредством скользящей средней. Сущность данного метода заключается в том, что рассчитывается средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем — из такого же числа уровней, но начи­ная со второго по счету, далее — начиная с третьего и т.д.

Рассмотренные способы позволяют выявить тренд для его описания, но получить обобщающую статистическую оценку тренда этими подходами невозможно. Поэтому для измерения тренда используется метод аналитического выравнивания.Суть данного метода заключается в том, что фактические уровни ряда заменяются плавными уровнями, вычисленными на основе определенной линии (прямой или кривой), выбранной в предположении, что она точнее всего отображает общую тенденцию явления.

В основе метода лежит установление функциональной зависимости уровней ряда от времени. При этом на практике чаще всего применяются математические функции такого вида:

1) линейная:

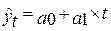
2) параболическая:

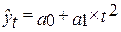
3) гиперболическая:

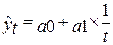
4) степенная:

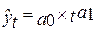
где - параметры, которые находятся методом наименьших квадратов

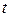- порядковый номер периода.

На основе теоретического анализа выявляется характер развития явления во времени, и на этой основе выбирается тот или другой вид аналитической функции. Практикой установлено, что принятие соответствующей аналитической функции осуществляется при следующих условиях:

1) выравнивание по уравнению прямой линии целесообразно, если цепные абсолютные приросты более или менее постоянны, т.е. уровни изменяются в арифметической прогрессии.

2) выравнивание по параболической функции необходимо выполнять в тех случаях, когда изменение уровней ряда происходит с приблизительно равным ускорением или замедлением цепных абсолютных приростов.

3) выравнивание по степенной функции целесообразно использовать тогда, когда уровни ряда выявляют тенденцию постоянства цепных темпов роста, т.е. в случае изменения уровней ряда динамики в геометрической прогрессии.

В случае линейной зависимости параметры функции находиться решением следующей системы нормальных уравнений:

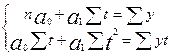
Расчет параметров можно значительно упростить, если отсчет времени 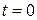осуществлять с середины ряда динамики. Для того, чтобы сумма показателей времени равнялась нулю, условные обозначения нужно давать таким образом:

1) при нечетном числе уровней ряда динамики, уровень в середине ряда приравнивают к нулю, а уровни, расположенные выше него, помечают числами со знаком ''минус'' (-1,-2 и т.д.), а ниже – числами со знаком ''плюс'' (+1,+2 и т.д.)

2) при четном числе уровней ряда динамики уровни, которые лежат выше среднего значения, находящегося между двумя средними датами, помечают числами со знаком ''минус'' (-1,-3,-5 и т.д.), а ниже среднего значения – числами со знаком ''плюс'' (+1,+3,+5 и т.д.)

В обоих случаях 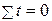, так что система нормальных уравнений принимает вид:

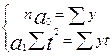
Отсюда следует. что

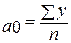
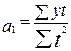
В практической деятельности может возникнуть необходимость интерполяции или экстраполяции рядов динамики. Самым совершенным при этом является выравнивание по определенному аналитическому уравнению.

Интерполяция– это нахождение отсутствующих промежуточных уровней ряда динамики.

Экстраполяция используется при прогнозировании социально-экономических явлений и процессов в будущем с предположением, что выявленная тенденция будет сохраняться и в дальнейшем за пределами исследуемого ряда динамики.

Дата добавления: 2014-03-11; просмотров: 713; Нарушение авторских прав

Мы поможем в написании ваших работ!