
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вопрос 3. Непараметрические методы
Регрессионный анализ
Корреляционный анализ
Вопрос 2. Статистические методы моделирования связи
Для изучения функциональных связей применяются балансовый и индексный методы.
Для исследования стохастических связей широко используются следующие методы:
1. Метод сопоставления параллельных рядовзаключается в том, что факторы, Характеризующие результативный признак располагают в возрастающем или убывающем порядке, а затем прослеживают изменение величины результативного показателя. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяют установить наличие связи и ее направление.
Недостатком данного метода является невозможность определения количественной меры связи между изучаемыми признаками.
2. Метод аналитических группировоксостоит в том, чтоединицы изучаемой совокупности группируют по факторному признаку и для каждой группы вычисляют среднее или относительное значение результативного признака. Затем сопоставляя изменения результативного признака по мере изменения факторного, можно выявить направление, характер и тесноту связи между ними с помощью эмпирического корреляционного отношения. Однако данный метод не позволяет определить форму, т.е.аналитическое выражение, влияния факторных признаков на результативный.
Статистические методы моделирования связи требуют, чтобы все признаки были количественно измеримы. Вместе с тем в статистике применяются также непараметрические методы, с помощью которых устанавливается связь между атрибутивными (качественными) признаками. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерения ее тесноты.
В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположенными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциациии коэффициент контингенции.
Для их расчета строится четырех клеточная корреляционная таблица, которая носит название таблицы ‘’четырех полей ‘’ и имеет следующий вид:
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+c+b+d |
Применительно к таблице ‘’четырех полей ‘’ с частотами a, c, b и d коэффициент ассоциациивыражается формулой:
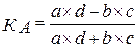
Данный коэффициент изменяется от – 1 до +1. Чем значение коэффициента ближе к предельным значениям, тем сильнее связаны между собой изучаемые признаки, если коэффициент ассоциации не менее 0,3, то это свидетельствует о наличии связи между качественными признаками.
В случаях, когда один из показателей таблицы ‘’четырех полей ‘’ отсутствует. Величина коэффициента ассоциации будет равен единице. В этом случае необходимо рассчитывать коэффициент контингенции:
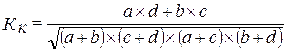
Данный коэффициент изменяется от – 1 до +1. Чем значение коэффициента ближе к предельным значениям, тем теснее связаны между собой изучаемые признаки.
Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с показателя взаимной сопряженности А.А. Чупрова:
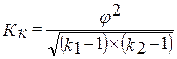
где К1 - число возможных значений первой статистической величины (число групп по столбцам);
К2 - число возможных значений второй статистической величины (число групп по строкам);
φ 2 - показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки, затем вычитается единица.
Коэффициент взаимной сопряженности Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков.
Для определения связи как между количественными, так качественными признаками при условии, что значения этих признаков ранжированы, может быть использован коэффициент корреляции рангов Спирмена (коэффициент ранговой корреляции). Рангами называют числа натурального ранга, которые представляются в баллах по определенным критериям элементов совокупности. При этом ранжирование проводится по каждому признаку отдельно: первый ранг присваивается наименьшему значению признака. последний – наибольшему. Количество рангов равняется объему совокупности.
Коэффициент корреляции рангов Спирменарассчитывается по формуле:

где dj - разность между рангами по одному и другому признаку
п - количество единиц в ряду
Для предварительной оценки тесноты связи между атрибутивными признаками используются коэффициенты конкордации Фехнера и Кендела.
| <== предыдущая страница | | | следующая страница ==> |
| Вопрос 1. Виды связей между явлениями | | | Вопрос 1. Регрессионный анализ |
Дата добавления: 2014-03-11; просмотров: 520; Нарушение авторских прав

Мы поможем в написании ваших работ!