Вопрос 1. Регрессионный анализ

ТЕМА № 8.2. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

(4 часа)

1. Регрессионный анализ

2. Корреляционный анализ

Изучение корреляционной связи между признаками начинается с регрессионного анализа, который решает проблему установления формы связи, вида уравнения регрессии, определенияпараметров уравнения регрессии.

В регрессионном анализе различают уравнения парной и множественной регрессии. Рассмотрим уравнение парной регрессии, как наиболее простой случай связи между признаками, что достаточно широко используется в статистической практике исследования социально-экономических явлений.

Наиболее часто для характеристики корреляционной связи между признаками используют следующие виды уравнений парной регрессии:

5) линейный:

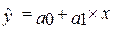
6) параболический:

7) гиперболический:

8) степенной:

где - параметры уравнений регрессии, которые подлежат определению

х - значение факторного признака.

Для выбора вида уравнения регрессии необходимо построить график зависимости фактических данных 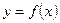и по расположению точек на графике установит визуально, к какому виду можно отнести линию регрессии.

Параметры в уравнениях регрессии определяются методом наименьших квадратов, который предполагает решение определенной системы нормальных уравнений.

В случае линейнего вида уравнения регрессии система нормальных уравнений записывается в виде:

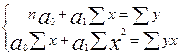
где п - количество единиц совокупности

Для решения данной системы, находим значения параметров по следующим формулам:

;

или

;

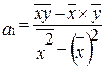
где 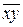- средняя из произведения факторного признака на результативный;

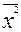- средняя из суммы квадратов факторного признака;

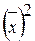- квадрат средней из факторного признака.

В уравнении регрессии параметр экономического смысла не имеет. Параметр 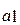называется коэффициентом регрессии и показывает изменение результативного признака при изменении факторного признака на единицу.

Для оценки влияния факторного признака на результативный может рассчитываться коэффициент эластичности в среднем для всей совокупности:

где , - средние величины фактических данных соответственно по факторному и результативному признаку в целом по всей совокупности.

Коэффициент эластичности показывает, на сколько процентов в среднем измениться результативный признак при изменении факторного признака на 1%.

В случае использования параболического вида уравнения регрессии система нормальных уравнений имеет следующий вид:

Дата добавления: 2014-03-11; просмотров: 366; Нарушение авторских прав

Мы поможем в написании ваших работ!