
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Метод математической индукции
Аксиома индукции лежит в основе доказательств методом математической индукции, который имеет несколько разновидностей.
Теорема 1(принцип математической индукции). Если некоторое высказывание с переменным 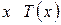 (одноместный предикат), определенное на множестве
(одноместный предикат), определенное на множестве 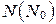 , удовлетворяет следующим условиям: a)
, удовлетворяет следующим условиям: a) 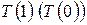 истинно; b) для каждого
истинно; b) для каждого 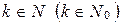 из
из 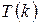 истинно следует, что истинно
истинно следует, что истинно 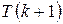 . Тогда
. Тогда 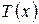 истинно для любого натурального
истинно для любого натурального 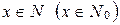 .
.
Д.: Докажем для множества 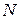 . Через
. Через 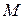 обозначим множество натуральных чисел из
обозначим множество натуральных чисел из 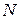 , для которых
, для которых 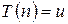 , т.е.
, т.е. 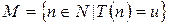 . Из выполнимости условий a) и b) следует: а)
. Из выполнимости условий a) и b) следует: а) 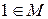 ; б) для любого
; б) для любого 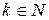 , если
, если 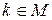 , то
, то 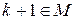 . Тогда по аксиоме индукции (6) следует
. Тогда по аксиоме индукции (6) следует 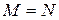 , т.е.
, т.е. 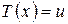 , для любого
, для любого 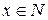 .
.
Аналогично доказывается для множества 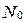 (докажите самостоятельно).
(докажите самостоятельно).
Доказательство по индукции состоит из двух этапов: 1) доказывается, что 1 (0) удовлетворяет условию 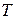 , т.е.
, т.е. 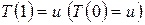 (база индукции); 2) доказывается, что для всякого
(база индукции); 2) доказывается, что для всякого 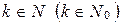 из
из 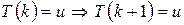 (достоверность индуктивного шага).
(достоверность индуктивного шага).
Приведем еще две теоремы без доказательств, относящихся к методу математической индукции.
Теорема 2 (усиленный принцип математической индукции). Если некоторое высказывание с переменным 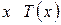 , определенное на множестве
, определенное на множестве 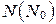 , удовлетворяет следующим условиям: a)
, удовлетворяет следующим условиям: a) 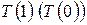 истинно; b) для каждого
истинно; b) для каждого 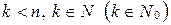 из
из 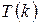 истинно следует, что
истинно следует, что 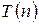 истинно. Тогда
истинно. Тогда 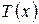 истинно для любого натурального
истинно для любого натурального 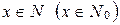 .
.
В доказательстве используется теорема 1. Докажите самостоятельно.
Доказательство усиленным методом математической индукции состоит также из двух этапов:
1) доказывается, что 1 (0) удовлетворяет условию 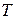 , т.е.
, т.е. 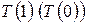 истинно (база индукции);
истинно (база индукции);
2) предполагается, что для всякого 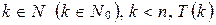 - истинно, и доказывается, что
- истинно, и доказывается, что 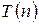 также истинно (справедливость индуктивного шага).
также истинно (справедливость индуктивного шага).
Теорема 3 (обобщенный принцип математической индукции). Если некоторое высказывание 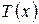 с переменной
с переменной 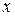 , определенное на множестве натуральных чисел
, определенное на множестве натуральных чисел 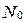 , удовлетворяет следующим условиям: a)
, удовлетворяет следующим условиям: a) 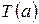 истинно,
истинно, 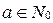 ; b) для каждого
; b) для каждого 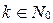 , где
, где 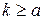 ,
, 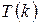 истинно следует, что
истинно следует, что 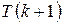 истинно, тогда
истинно, тогда 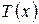 истинно для любого натурального числа
истинно для любого натурального числа 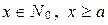 .
.
Доказательство обобщенным принципом математической индукции, как и выше, состоит из двух шагов:
1) доказывается, что некоторое число 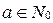 удовлетворяет условию
удовлетворяет условию 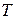 , т.е.
, т.е. 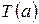 истинно (база индукции);
истинно (база индукции);
2) предполагается, что для всякого 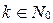 , где
, где 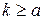 ,
, 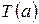 истинно, и доказывается, что
истинно, и доказывается, что 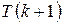 также истинно (достоверность индуктивного шага).
также истинно (достоверность индуктивного шага).
Пример 1. Найти сумму первых 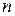 нечетных чисел натурального ряда, т.е.
нечетных чисел натурального ряда, т.е. 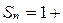
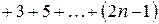 , где
, где 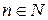 , т.е.
, т.е. 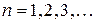 .
.
Решение. Иногда для нахождения предполагаемого результата пользуются так называемой неполной индукцией, т.е. находят значения искомого выражения для некоторых первых значений 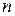 . Вычисляя непосредственно значения
. Вычисляя непосредственно значения 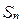 при
при 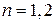 и 3, будем иметь:
и 3, будем иметь: 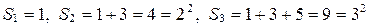 . Учитывая, что
. Учитывая, что 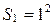 , можно сделать предположение:
, можно сделать предположение: 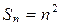 . Для доказательства справедливости высказанного предположения воспользуемся индукцией.
. Для доказательства справедливости высказанного предположения воспользуемся индукцией.
a) 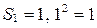 , база индукции верна;
, база индукции верна;
b) Пусть утверждение верно для произвольного 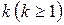 , т.е.
, т.е. 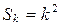 или
или 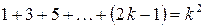 . Докажем для
. Докажем для  .
. 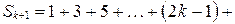
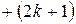 или
или 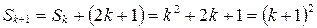 . Таким образом,
. Таким образом, 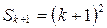 . По теореме 1
. По теореме 1 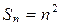 для любого
для любого 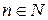 .
.
Пример 2. Доказать, что для любого натурального числа 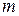 , где
, где 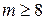 , можно найти такие неотрицательные числа
, можно найти такие неотрицательные числа 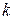 и
и 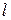 , что выполняется равенство
, что выполняется равенство 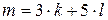 , причем для некоторых
, причем для некоторых 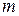 одно из чисел
одно из чисел 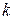 или
или 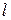 может равняться нулю.
может равняться нулю.
Решение. Воспользуемся обобщенным принципом математической индукции:
a) 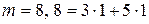 или
или 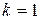 и
и 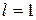 , база индукции верна. Отметим, что 8 – наименьшее число, для которого данное утверждение должно быть справедливым.
, база индукции верна. Отметим, что 8 – наименьшее число, для которого данное утверждение должно быть справедливым.
b) Предположим, что требуемое соотношение справедливо для произвольного числа 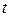 , где
, где 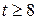 , т.е. существуют такие неотрицательные целые числа
, т.е. существуют такие неотрицательные целые числа 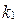 и
и 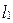 , что справедливо равенство
, что справедливо равенство 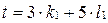 . Докажем справедливость утверждения для числа
. Докажем справедливость утверждения для числа 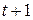 . Возможны два случая:
. Возможны два случая:
1) 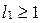 , тогда
, тогда 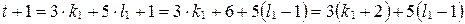 , где
, где 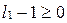 .
.
2) 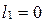 , т.к.
, т.к. 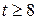 , то наименьшее предполагаемое
, то наименьшее предполагаемое 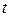 может быть не меньше 9, т.е.
может быть не меньше 9, т.е. 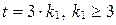 . Тогда
. Тогда 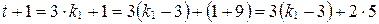 , где
, где 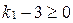 .
.
Согласно теореме 3 справедливость данного утверждения доказана.
Исходя из аксиоматического определения множества натуральных чисел, можно доказать, что для сложения и умножения натуральных чисел выполняются все свойства этих операций, известные из школьного курса математики.
Отношение порядка на множестве натуральных чисел 
О. Для натуральных чисел  и
и  говорят, что «
говорят, что « меньше
меньше  », и пишут
», и пишут 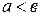 , если существует натуральное число
, если существует натуральное число 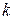 , что
, что 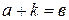 .
.
Говорят, что « меньше или равно
меньше или равно  », и пишут
», и пишут 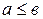 , если
, если 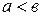 или
или 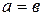 .
.
Отношение, инверсное к отношению 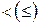 , обозначают символом
, обозначают символом 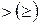 , т.е.
, т.е. 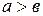
 тогда и только тогда, когда
тогда и только тогда, когда 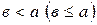 .
.
Для отношения порядка выполняются следующие свойства:
1) система 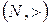 является вполне упорядоченным множеством, т.е. она линейно упорядочена и любое непустое подмножество множества натуральных чисел имеет наименьший элемент;
является вполне упорядоченным множеством, т.е. она линейно упорядочена и любое непустое подмножество множества натуральных чисел имеет наименьший элемент;
2) для любых натуральных чисел  и
и  , если
, если 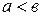 , то
, то 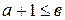 (свойство дискретности);
(свойство дискретности);
3) отношение 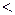 монотонно относительно сложения и умножения, т.е. для любых натуральных чисел
монотонно относительно сложения и умножения, т.е. для любых натуральных чисел  ,
,  и
и 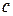
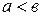 тогда и только тогда, когда
тогда и только тогда, когда 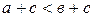 и
и 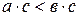 .
.
4) свойство архимедовости: для любых натуральных чисел  и
и  найдется такое натуральное число
найдется такое натуральное число 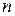 , что
, что 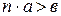 .
.
Отметим, что свойства натуральных чисел и вопросы, относящиеся к другим основным числовым системам, будут более детально изучены в специальной дисциплине «Числовые системы».
| <== предыдущая страница | | | следующая страница ==> |
| Натуральные числа | | | Целые числа |
Дата добавления: 2014-03-11; просмотров: 634; Нарушение авторских прав

Мы поможем в написании ваших работ!