Натуральные числа

В математике существуют два подхода к понятию множества натуральных чисел: при первом подходе считают натуральный ряд начинающимся с единицы 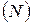, при втором подходе, в частности, в математической логике – начинающимся с нуля 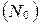, и определяют аксиоматически, при этом обычно пользуются модификациями системы аксиом, предложенной итальянским математиком-логиком Пеано (1858-1932).

При первом подходе под системой натуральных чисел 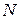понимают алгебру 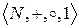, состоящую из некоторого множества 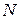, элементы которого называются натуральными числами, выделенного в 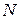элемента 1, бинарных операций 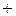(сложения) и 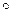(умножения), удовлетворяющих следующим условиям (аксиомам):

1. Для любого .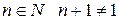

2. Для любых , если , то .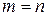

3. Для любых 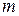и 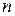выполняется равенство 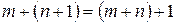(слабая форма ассоциативности сложения).

4. Для любого .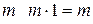

5. Для любых 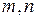из 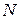имеет место равенство 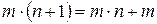(слабая форма дистрибутивности умножения относительно сложения).

6. (Аксиома индукции). Если 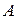- некоторое подмножество множества 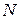такое, что а) 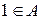, б) для любого 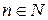, если 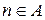, то 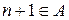, тогда имеет место равенство .

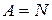При втором подходе под системой натуральных чисел 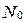понимают алгебру 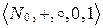, состоящую из некоторого множества 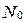, элементы которого называются натуральными числами, выделенных в 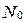элементов 0 и 1, бинарных операций 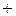(сложения) и 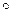(умножения), удовлетворяющих следующим условиям [3]:

1) Для любого .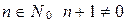

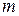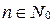2) Для любых и из .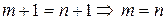

3) .

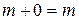4) .

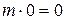5) .

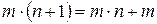6) (Аксиома индукции). Если 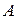- некоторое подмножество множества 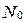такое, что а) 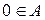, б) для любого 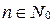, если 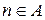, то 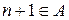, тогда имеет место .

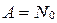Мы будем придерживаться первого подхода к системе натуральных чисел.

Дата добавления: 2014-03-11; просмотров: 265; Нарушение авторских прав

Мы поможем в написании ваших работ!