
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Целые числа
Натуральные числа используются для количественной характеристики совокупностей, состоящих из отдельных предметов, с их помощью можно характеризовать и другие явления, например, моменты времени. Но их недостаточно для практических потребностей, например, для измерения температуры.
В математике мы часто встречаемся с необходимостью нахождения решений разного рода уравнений. Но, если ограничиться лишь совокупностью натуральных чисел, то в ней неразрешимо даже простейшее уравнение такое, как 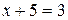 . Но их недостаточно и для практических потребностей, например, для характеристики численных значений величины, меньших некоторого выбранного начала отчета и т.п. Поэтому возникает необходимость расширения множества натуральных чисел.
. Но их недостаточно и для практических потребностей, например, для характеристики численных значений величины, меньших некоторого выбранного начала отчета и т.п. Поэтому возникает необходимость расширения множества натуральных чисел.
С точки зрения математики основным требованием такого расширения является то, чтобы в новом множестве было бы выполнимо действие, обратное сложению – вычитание.
Обозначим через 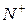 множество натуральных чисел и введем новое множество
множество натуральных чисел и введем новое множество 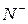 символов вида
символов вида 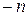 для всевозможных
для всевозможных 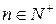 и назовем их противоположными натуральным:
и назовем их противоположными натуральным: 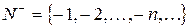 .
.
О. Множеством целых чисел называется множество
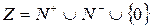 ,
,
т.е. множество, состоящее из натуральных чисел, нуля и чисел, противоположных натуральным.
Целые числа из 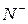 называются иначе целыми отрицательными числами, а из
называются иначе целыми отрицательными числами, а из 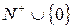 - целыми неотрицательными. (Отметим, что для любого целого числа имеем
- целыми неотрицательными. (Отметим, что для любого целого числа имеем 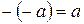 .)
.)
На множестве 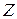 вводятся операции сложения и умножения и понятие модуля или абсолютной величины следующим образом.
вводятся операции сложения и умножения и понятие модуля или абсолютной величины следующим образом.
О. Модулем целого числа  , обозначаемым через
, обозначаемым через 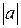 , называется число
, называется число 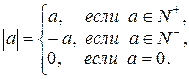
О. Для любых 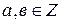 сумма
сумма 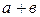 определяется согласно следующим правилам:
определяется согласно следующим правилам:
1) Если 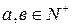 , то
, то 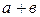 в
в 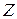 совпадает с суммой этих чисел, определенной в
совпадает с суммой этих чисел, определенной в 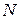 ;
;
2) 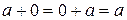 ;
;
3) Если 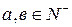 , то
, то  ;
;
4) При 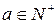 и
и 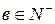 , т.е.
, т.е. 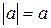 и
и 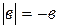 или
или 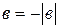 , возможны несколько случаев:
, возможны несколько случаев:
a) 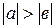 , тогда
, тогда 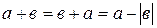 ;
;
b) 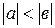 , тогда
, тогда 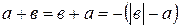 , учитывая, что
, учитывая, что 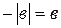 и
и 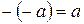 ;
;
g) 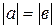 , тогда
, тогда 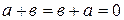 (напомним, что
(напомним, что 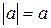 ,
, 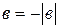 и
и 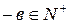 ).
).
Из определения суммы в 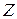 непосредственно следует, что сложение коммутативно. Можно доказать, что сложение подчиняется и ассоциативному закону.
непосредственно следует, что сложение коммутативно. Можно доказать, что сложение подчиняется и ассоциативному закону.
Покажем, что во множестве целых чисел для любых 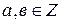 разрешимо уравнение
разрешимо уравнение 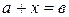 .
.
Действительно, решением является число 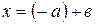 или
или 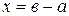 ,
, 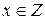 , т.к.
, т.к. 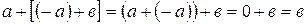 , причем такое число единственное. Число
, причем такое число единственное. Число 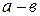 называют разностью чисел
называют разностью чисел  и
и  .
.
Любое целое число 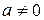 принадлежит
принадлежит 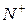 или
или 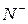 , т.е.
, т.е.  или
или  ,
, 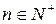 . Соответствующий числу
. Соответствующий числу  знак назовем его знаком и будем обозначать
знак назовем его знаком и будем обозначать 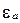 , нулю приписывают любой из знаков + или -. Тогда имеет место соотношение
, нулю приписывают любой из знаков + или -. Тогда имеет место соотношение 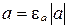 или
или 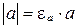 .
.
Определим умножение знаков следующим образом:
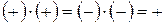 ;
; 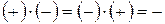 .
.
О. Для любых 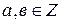 произведение
произведение 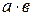 определяется следующим образом:
определяется следующим образом:
1) если одно из чисел  или
или  равно нулю, то
равно нулю, то  ;
;
2) в общем случае  .
.
Согласно определению произведения знаков имеем 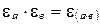 .
.
Упр. 17. Доказать, что 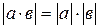 .
.
Можно доказать, что во множестве 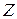 выполняются коммутативный и ассоциативный законы умножения и дистрибутивный закон умножения относительно сложения.
выполняются коммутативный и ассоциативный законы умножения и дистрибутивный закон умножения относительно сложения.
Таким образом, как отмечено выше, множество целых чисел является коммутативным кольцом с единицей.
Существует и другой подход к определению понятия целого числа.
О. Целым числом называют разность двух натуральных чисел, т.е. 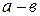 , где
, где  и
и  произвольные натуральные числа.
произвольные натуральные числа.
Известно, что для натуральных чисел  и
и  всегда выполняется и причем только одно из трех соотношений:
всегда выполняется и причем только одно из трех соотношений:
1) существует натуральное число 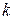 , что
, что 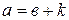 ;
;
2) существует натуральное число 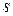 , что
, что  ;
;
3) 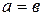 .
.
В первом случае 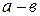 во множестве
во множестве 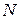 определено и равно
определено и равно 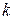 , т.е.
, т.е. 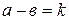 . Во втором случае
. Во втором случае 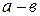 во множестве
во множестве 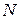 не определено, обозначим эту разность через
не определено, обозначим эту разность через 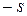 и назовем его числом, противоположным
и назовем его числом, противоположным 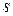 . В третьем случае разность
. В третьем случае разность 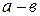 обозначим символом 0 (нуль).
обозначим символом 0 (нуль).
Таким образом, получим новое множество чисел, состоящее из натуральных чисел, противоположных натуральным и нуля. Это множество назовем множеством целых чисел.
При таком подходе довольно просто определяются операции сложения и умножения целых чисел, но возникают трудности другого характера, связанные с тем, что одно и то же число может быть представлено в виде разностей различных пар чисел, например, число 3 можно представить в виде разностей 6-3, 12-9, 23-20 и т.д., -5 – в виде 5-10, 20-15, 95-100 и т.д.
Мы будем придерживаться первого подхода к определению целого числа.
| <== предыдущая страница | | | следующая страница ==> |
| Метод математической индукции | | | Отношение порядка на множестве целых чисел |
Дата добавления: 2014-03-11; просмотров: 267; Нарушение авторских прав

Мы поможем в написании ваших работ!