Основные закономерности процесса испарительного охлаждения воды в градирнях

Градирни относятся к категории теплообменных аппаратов, в которых теплоноситель—вода—отдает тепло охлаждающему агенту—воздуху—не через стенку, а путем непосредственного контакта.

В виду сложности процессов тепломассообмена в градирнях тепловой расчет их долгое время основывался на так называе­мых эмпирических «графиках охлаждения». За последнее время все более широкое применение находят методы теплового рас­чета градирен по формулам теории испарительного охлаждения.

Количество тепла, отдаваемое теплоносителем охлаждающе­му агенту в градирнях, так же как и в обычных теплообменных аппаратах, пропорционально поверхности теплообмена. Под по­верхностью теплообмена в градирне следует понимать общую поверхность всех капель и пленок воды, вступающих в соприкос­новение с воздухом. В соответствии с этим при вычислении по­верхности охлаждения градирни следовало бы включить боко­вые поверхности щитов, планок, стоек, реек, связок раскосов и др., омываемых водой между водораспределителем и уровнем воды в водосборном резервуаре, а также поверхности всех ка­пель и струек воды во всем этом про­странстве. Однако такое определение поверхности теплообмена сопряжено с большими трудностями и, вообще го­воря, практически невозможно, так как нельзя с достаточной степенью точности учесть количество и размеры капель и струек воды при различных конструкциях водораспределителей и оросителей и разных скоростях движе­ния воздуха в градирне. Поэтому для пленочных градирен допускается неко­торая условность: в качестве поверх­ности теплообмена принимается боко­вая поверхность щитов оросителя, предполагая, что эта часть поверхно­сти теплообмена составляет наиболь­шую долю.

Для получения основных законо­мерностей испарительного охлаждения

рассматривается стационарный процесс тепломассообмена в про­стейшей пленочной градирне, в которой вода и воздух приводят­ся в непосредственный контакт друг с другом по схеме противо­тока ( см. рис.10.3).

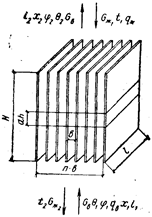
Рис.10.13 Схема теплового и материального баланса пленочной градирни

Горячая вода со средней температурой t₁,°C, в количестве G_ж1, кг/с, с постоянной плотностью орошения

q_ж= G_ж1/F_op(*)

поступает в верх градирни, равномерно растекаясь в виде плен­ки по боковым поверхностям щитов (для создания более разви­той поверхности соприкосновения воды с воздухом). В формуле (*) F_op—площадь элемента оросителя градирни в плане, м²:

F_op=nbl,

где п, b и l указаны на рис. 10.3.

Некоторое количество водыG_и испаряется в градирне. Оставшаяся часть воды G_ж2=G_ж1 - G_и ,со средней температурой t₂ более низкой, чем t₁, поступает в низ градирни. В градирню снизу входит G_в._с, кг/с, сухого воздуха или G_в=G_в.с(1+x₁)

влажного воздуха со средней температурой θ₁°C, относи­тельной влажностью φ₁, % (или доли единицы), влагосодержанием х₁, кг/кг, энтальпией i₁, Дж/кг (величины влагосодержания и энтальпии отнесены к 1 кг сухого воздуха в соответствии с обозначением Молье), и постоянной массовой скоростью .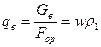

Количество влаги в воздухе, выходящем из градирни, увели­чивается на количество испарившейся воды G_и ; при этом, по ме­ре движения воздуха снизу вверх по оросителю градирни тем­пература, влагосодержание и энтальпия его изменяются (увели­чиваются).

Выделив по высоте градирни элементарный горизонтальный слой высотой dh (см. рис. 10.13), составим для него уравнение теп­лового баланса, устанавливающее равенство между теплом, по­терянным сплошной водной пленкой с поверхности щитов в еди­ницу времени, и теплом, которое приобрел воздух за то же время при непосредственном увеличении его температуры и влаго­содержания за счет проникновения в него пара в результате ис­парения воды.

При составлении уравнения теплового баланса делаются сле­дующие допущения, которые, как указывает Л. Д. Берман, незначительно отражаются на конечном результате испарительно­го охлаждения воды в условиях градирен.

1. Коэффициенты теплоотдачи α_f, Вт/(м²K), и массоотдачи β_pf, кг/(м²ч), физические величины—теп­лота парообразования r, Дж/кг, и удельная теплоемкость влаж­ного воздуха С_в._вл, Дж /(кг°С), могут быть приняты постоянны­ми для всей поверхности охлаждения, так как колебания их зна­чений весьма незначительны при изменениях температуры воды и воздуха.

2. Парциальное давление водяного пара Р_пθ в пределах гра­дирни весьма мало в сравнении с очень незначительно меняю­щимся полным давлением влажного воздуха Р_б, и величина парциального давления сухой части воздуха Р_в._сθ может быть принята постоянной.

3. Количество испаряющейся воды незначительно и может быть принято, что G_ж1 ~= G_ж.

4. Температура на поверхности пленок воды в данном сече­нии градирни может быть принята равной средней температуре воды в том же сечении. При малых значениях удельного тепло­вого потока, отнесенного к единице поверхности контакта воды с воздухом, и интенсивном перемешивании жидкости, что харак­терно для градирен, можно с достаточной для практических рас­четов точностью это условие принять при выводе основных рас­четных зависимостей.

Количество тепла, потерянного водяной пленкой с обеих сто­рон каждого щита в пределах выделенного слоя градирни в еди­ницу времени, составляет

dQ = 2lq_o с_ж п ∂t/∂n dh,

где q_o — количество воды, приходящееся на 1 м верхней кромки щита с одной стороны, кг/(м·с); t - температура воды, °С; c_ж—удельная теплоемкость воды, Дж/(кг°С); h—высота оро­сителя, м; п—количество щитов за вычетом единицы.

Количество тепла, отнимаемого от воды соприкосновением в единицу времени и затраченного на увеличение температуры воздуха:

dQ_α=blq_вс_вn(∂θ/∂h)dh

где c_в—удельная теплоемкость воздуха, Дж/(кг°С), θ—температура воздуха, °С.

Количество тепла, отводимого от воды испарением в едини­цу времени и затраченного на увеличение влагосодержания воз­духа:

dQ_β≈r_odG_ж= blq_вr_on(∂x/∂h)dh.

Составляя затем уравнение тепловогобаланса, получим

dQ=dQ_α+dQ_β.

После соответствующих преобразований полученное выраже-ние можно представить в следующем виде: dQ = G_жc_ж dt = G_в(с_вdθ+r_odx), (**)

где Gж=2lq_on ;G_в= blq_вn

Выражение, стоящее в скобках правой части уравнения (**), представляет собой приращение энтальпии воздуха в пределах рассматриваемого слоя градирни:

di=c_вdθ+r₀dx;

тогда dQ=G_жс_жdt=G_вdi.

Из равенства, учитывающего количество тепла, отводимого от воды соприкосновением, согласно формуле Ньютона, можно написать:

dQ_α, = α_f(t — θ),

где α_f - коэффициент теплоотдачи, Вт/(м² С). Обозначив через df_oхл поверхность охлаждения в пределах выделенного элементарного слоя градирни высотой dh (см. рис. 10.13)

df_охл == 2lndh,

После подстановки получим

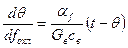
Определяя количество тепла, отнимаемого от воды испарени­ем, с использованием уравнения Дальтона, можно написать:

dQ_β=β_pf(P"_пt-P_по)r₀ = 2lndh

где β_pf - коэффициент массоотдачи, отнесенный к разности пар­циальных давлений, кг/(м²·с·Па); Р"_nt—парциальное давление пара на поверхности жидкости, Па; Р_пθ—парциальное давле­ние пара в ядре потока воздуха, Па.

Приращение влагосодержания в пре­делах выделенного слоя градирни можно представить следую­щим образом:

dx=0.622dP_пθ. / P_в._с.ср.

После преобразований получаем

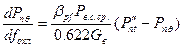
Подставляя значения dQ, dQ_a и dQ_β и осле соответствующих преобразований получим

.

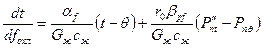Линейные дифференциальные уравнения первого порядка могут быть использованы для решения задачи по определению поверхности охлаждения градирни f_oхл, м², при заданных температурах воды и параметрах атмосферного воз­духа или для оценки охладительного эффекта градирни при за­данной поверхности, хотя решение этих уравнений сопряжено со значительными трудностями.

Дата добавления: 2014-03-11; просмотров: 502; Нарушение авторских прав

Мы поможем в написании ваших работ!