Передаточные функции фильтров

Активные RC-фильтры принадлежат к классу линейных схем с сосредоточенными параметрами. Передаточная функция линейной цепи n-го порядка с сосредоточенными параметрами описывается следующим выражением (порядок цепи определяется степенью полинома знаменателя):

T(s) = =,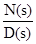

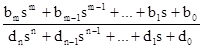где s — оператор Лапласа;

N(s) — полином числителя;

D(s) — полином знаменателя;

b_m…b₀ — вещественные коэффициенты полинома числителя;

d_n…d₀ — вещественные коэффициенты полинома знаменателя:

T(s) — передаточная функция схемы.

Заметим, что для реальных схем n³m.

Полиномы N(s) и D(s) можно разложить на множители первого и второго порядков с вещественными коэффициентами. Следовательно, нужную характеристику можно получить, включив последовательно несколько фильтров первого и второго порядков. Рассмотрим далее передаточные функции таких фильтров:

1. Характеристика ФНЧ первого порядка (рис. 2). Эта характеристика описывается простым выражением:

,

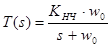где

К_НЧ - коэффициент передачи на постоянном токе,

w₀ - частота полюса, которая в данном случае равна частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с К_НЧ.

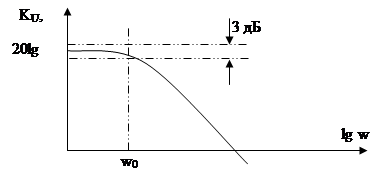
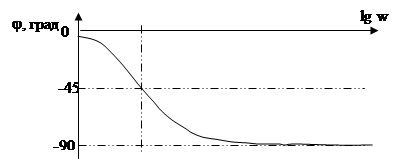
Рис. 2. Частотная характеристика ФНЧ первого порядка.

2. Характеристика ФВЧ первого порядка (рис.3). Эта характеристика также довольна простая

,

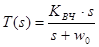где

К_ВЧ – коэффициент передачи на высоких частотах,

w₀ - частота полюса, на которой коэффициент передачи снижается на 3 дБ по сравнению с К_ВЧ.

3. Характеристика фазового фильтра (ФФ) первого порядка (рис. 4). Коэффициент передачи этого фильтра имеет постоянное значение во всем частотном диапазоне, изменяется лишь вносимый фазовый сдвиг (временная задержка).

Характеристика фазового фильтра первого порядка:

,

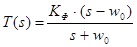где

К_Ф – модуль коэффициента передача,

w₀ - частота, на которой фазовый сдвиг равен 90^о.

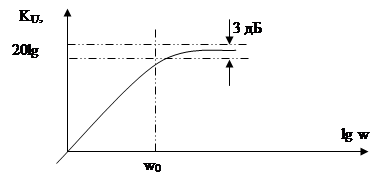
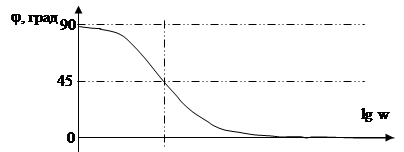
Рис. 3. Частотная характеристика ФВЧ первого порядка.

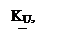
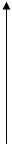
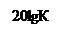
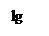
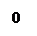
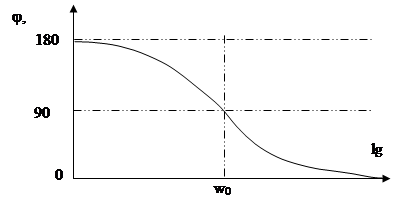
Рис. 4. Частотная характеристика ФФ первого порядка.

4. Характеристика ФНЧ второго порядка (рис. 5). Эта характеристика имеет вид:

,

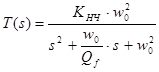где

К_НЧ – коэффициент передачи на постоянном токе,

w₀ - частота полюса,

Q_f - добротность фильтра.

При Q_f>1\2 на амплитудно-частотной характеристике (АЧХ) появляется выброс на частоте:

при больших Q_f,

и значение коэффициента передачи на этой частоте:

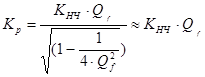при больших Q_f,

причем частота среза по уровню –3дБ составляет:

.

Для ФНЧ, характеристика которого показана на рис. 5, при малых Q_f (т.е. Q_f<1\2) полюса передаточной функции вещественные, и его АЧХ оказывается плоской. Выражение для характеристики второго порядка можно разложить на два сомножителя первого порядка. Когда же Q_f>1\2, на АЧХ появляется “выпуклость”. Амплитудно-частотная характеристика схем с большей добротностью имеет значительный выброс.

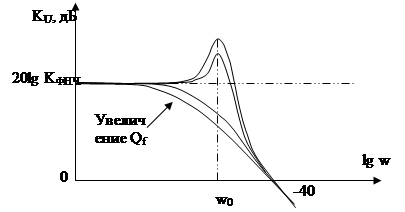
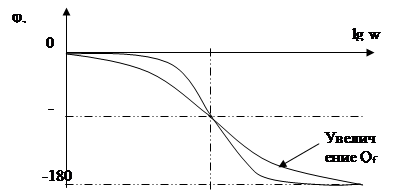
Рис. 5. Частотная характеристика ФНЧ второго порядка.

5. Характеристика ФВЧ второго порядка (рис. 6). Эта характеристика описывается выражением:

,

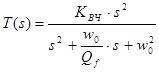где

К_ВЧ – коэффициент передачи на высокой частоте,

w₀ - частота полюса,

Q_f - добротность фильтра.

Максимальный коэффициент передачи (в точке выброса) при больших значениях Q_f равен К_ВЧ* Q_f.

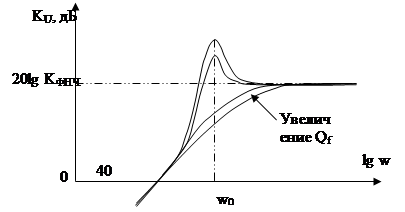
Рис. 6. Частотная характеристика ФВЧ второго порядка.

Выброс на АЧХ возникает при Q_f>1\2 на частоте:

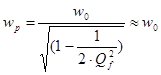при больших Q_f,

и значение коэффициента передачи при этом равно:

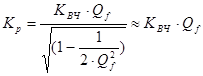при больших Q_f.

Частота среза по уровню –3дБ равна:

.

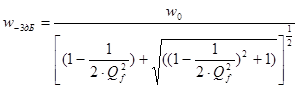6. Характеристика ПФ второго порядка (рис. 7). Эта характеристика описывается выражением:

,

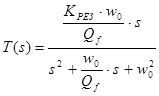ее можно представить в другом виде:

,

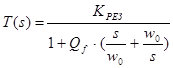где

К_РЕЗ - коэффициент передачи на центральной частоте w₀,

Q_f - добротность фильтра.

Заметим, что

Q_f=w₀/(w₂ – w₁),

где

w₁, w₂ – частоты, на которых коэффициент передачи снижается на –3дБ по сравнению с К_РЕЗ.

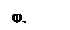
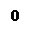
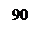
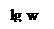
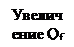
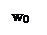
Рис. 7. Частотная характеристика ПФ второго порядка.

Можно показать, что:

,

,

.

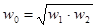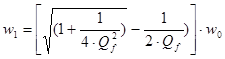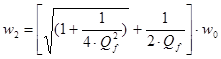Ширина полосы пропускания по уровню –3дБ составляет:

.

При малых добротностях (Q_f<1/2) знаменатель передаточной функции можно разложить на два сомножителя с вещественными коэффициентами (т.е. передаточная функция может быть представлена в виде произведения двух функций первого порядка), поэтому АЧХ и ФЧХ на рис. 7 выглядит досточно пологими. При Q_f>1/2 поляса передаточной функции становятся комплексными. С увеличением Q_f полоса пропускания сужается, и характеристика фильтра становится более избирательной.

7. Характеристика ППФ второго порядка (рис. 8). Передаточная функция описывается выражением:

,

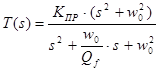где

К_ПР – коэффициент передачи на постоянном токе и на высокой частоте,

w₀ – центральная частота полосы подавления,

Q_f – добротность фильтра.

Приведенное выше выражение можно записать по-другому:

,

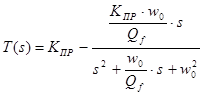т.е. в виде разности постоянного коэффициента передачи К_ПР и коэффициента передачи ПФ.

Частота среза по уровню –3дБ такие же, как у полосового фильтра:

,

.

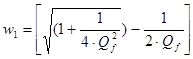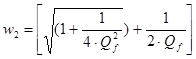Ширина полосы подавления по уровню –3дБ равна:

.

Рис. 8. Частотная характеристика ППФ.

8. Характеристика ФФ второго порядка (рис. 9). Характеристика ФФ второго порядка описывается выражением:

.

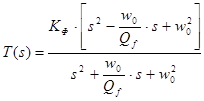Его можно представить в следующем виде:

,

т.е. постоянный коэффициент минус удвоенная передаточная характеристика полосового фильтра.

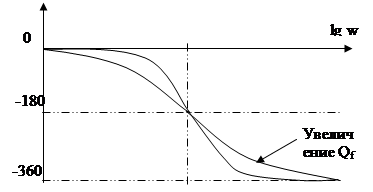
Рис. 9. Частотная характеристика ФФ второго порядка.

Дата добавления: 2014-03-13; просмотров: 504; Нарушение авторских прав

Мы поможем в написании ваших работ!