
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Определение требуемой передаточной функции
Проектирование фильтров высоких порядков
Имеется несколько типов передаточных функций с различными свойствами, со своими достоинствами и недостатками. Наиболее известны три типа передаточных функций: Баттерворта, Чебышева и Бесселя. Существуют и другие типы фильтров, за более подробными сведениями о них можно обратиться к специальной литературе.
Рассматриваемые далее типы фильтров считаются нормированными, т.е. их коэффициент передачи в полосе пропускания равен 1 (0 дБ), а частота среза — 1 рад/с. Для расчета других фильтров (полосовых, верхних частот и т.д.) необходимо провести операции преобразования частот и масштабирования, которые рассмотрены ниже.
Фильтры Баттерворта (с максимально плоской характеристикой).
Эти фильтры отличаются наибольшей равномерностью АЧХ как в полосе пропускания, так и в полосе подавления. Поскольку на АЧХ отсутствуют пульсации (максимумы и минимумы), каждое значение коэффициента передачи появляется только один раз на конкретной частоте. Такое свойство называется монотонностью характеристики фильтра.
Спад АЧХ за полосой пропускания составляет 20n дБ/декада, где n — порядок фильтра. Максимально плоская АЧХ в полосе пропускания достигается за счет ухудшения линейности фазовой характеристики. Ее нелинейность приводит к фазовым искажениям, так как сигналы различных частот имеют разное время задержки. На переходной характеристике фильтра при этом появляется выброс и "звон" на вершине выходного импульса, величина которых возрастает при повышении порядка фильтра. Все корни передаточной функции ФНЧ Баттерворта являются полюсами, т.е. среди них нет нулей. Фильтр Батгерворта можно использовать как хороший фильтр общего назначения, поскольку он имеет максимально плоскую АЧХ, умеренную фазовую нелинейность, приемлемую переходную характеристику и достаточно крутой спад АЧХ вне полосы пропускания. Эти свойства делают его одним из наиболее широко применяемых фильтров.
Полиномы Баттерворта T(s) = 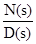 ,
,
где N(s) = 1;
D(s) представлены в табл. 2.
Таблица 2
| Порядок n | D(s) |
| (s + 1) | |
| (s2 + 1,41421s + 1) | |
| (s + l)(s2 + s + l) | |
| (s2 + 1,84776s + 1)(s2 + 0,76537s + 1) | |
| (s + 1)(s2 + 1,61803s + 1)(s2 + 0,61803s + 1) | |
| (s2 + 1,93185s + 1)(s2 + 1,41421s + 1) (s2 + 0,51764s + 1) | |
| (s + 1)(s2 + 1,80194s + 1)(s2 + 1,24698s + 1)(s2 + 0,44504s + 1) | |
| (s2 + 1,96157s + 1)(s2 + 1,66294s + 1)(s2 + 1,11114s + 1)(s2 + 0,39018s + 1) |
Фильтры Чебышева (фильтр равных пульсации).
Фильтр Чебышева характеризуется крутым спадом АЧХ и немонотонностью коэффициента передачи в полосе пропускания. Крутизна спада АЧХ достигается ценой появления существенных пульсации на характеристике в полосе пропускания. Их величина лежит между уровнями 0.1 и 3 дБ.
Более крутой спад приводит и к увеличению нелинейности фазовой характеристики в полосе пропускания. Следовательно, возрастают и величина перерегулирования, и звоны на вершине выходного перепада. Фильтры Чебышева также не содержат нулей в передаточной функции.
Фильтры Чебышева используются в тех случаях, когда требуется наиболее крутой спад АЧХ за частотой среза. Фазовую характеристику можно сделать более линейной, дополнив фильтр фазовращателем, но при этом увеличивается общее время задержки.
Полиномы фильтров Чебышева с пульсациями в полосе пропускания 0,5 дБ представлены в табл. 3.
Таблица 3
| n | N(s) | D(s) |
| 2,863 | (s + 2,863) | |
| 1,431 | (s2 + 1,426s + 1,516) | |
| 0,716 | (s + 0,626)(s2 + 0,626s +1,142) | |
| 0,358 | (s2 + 0,351s + 1,064)(s2 + 0,847s + 0,356) | |
| 0,1789 | (s + 0,362)(s2 + 0,224s + 1,036)(s2 + 0,586s + 0,477) | |
| 0,0895 | (s2 + 0,155s + 1,023)(s2 + 0,424s + 0,590)(s2 + 0,580s + 0,157) | |
| 0,0447 | (s + 0,256)(s2 + 0,114s + l,016)(s2 + 0,319s + 0,677)(s2 + 0,462s + 0,254) | |
| 0,0224 | (s2 + 0,0872s + 1,012)(s2 + 0,248s + 0,741)(s2 + 0,372s + 0,359)(s2 + 0,439s + 0,088) |
Полиномы фильтров Чебышева с пульсациями в полосе пропускания 1 дБ представлены в табл. 4.
Таблица 4
| n | N(s) | D(s) |
| 1,965 | (s +1,965) | |
| 0,983 | (s2 + l,098s + l,103) | |
| 0,491 | (s + 0,494)(s2 + 0,494s + 0,994) | |
| 0,246 | (s2 + 0,674s + 0,279)(s2 + 0,279s + 0,987) | |
| 0,123 | (s + 0,289)(s2 + 0,468s + 0,429)(s2 + 0,179s + 0,988) | |
| 0,0614 | (s2 + 0,124s + 0,991)(s2 + 0,340s + 0,558)(s2 + 0,464s + 0,125) | |
| 0,0307 | (s + 0,205)(s2 + 0,0914s + 0,993)(s2 + 0,256s + 0,653)(s2 +0,370s +0,230) | |
| 0,0154 | (s2 + 0,070s + 0,994)(s2 + 0,199s + 0,724)(s2 + 0,298s +0,341)(s2 + 0,352s + 0,0703) |
Полиномы фильтров Чебышева с пульсациями в полосе пропускания 3 дБ представлены в табл. 5.
Таблица 5
| n | N(s) | D(s) |
| (s + 1) | ||
| 0,500 | (s2 + 0,644s + 0,707) | |
| 0,250 | (s + 0,298)(s2 + 0,298s + 0,839) | |
| 0,125 | (s2 + 0,170s+ 0,903)(s2 + 0,410s + 0,196) | |
| 0,0625 | (s + 0,177)(s2 + 0,110s + 0,936)(s2 + 0,287s + 0,377) | |
| 0,0313 | (s2 + 0,0763s + 0,955)(s2 + 0,209s + 0,522)(s2 + 0,285s + 0,0887) | |
| 0,0156 | (s + 0,126)(s2 + 0,0562s + 0,966)(s2 + 0,157s + 0,627)(s2 + 0,228s + 0,204) | |
| 0,00781 | (s2+0,0431s+0,974)(s2+0,123s+0,704)(s2+0,184s+0,321)(s2+0,217s+0,0503) |
Фильтры Бесселя (фильтры с линейной фазовой характеристикой или фильтры Томсона).
Фильтры Бесселя имеют фазовую характеристику, максимально близкую к идеальной. Благодаря линейной фазовой характеристике, сигналы всех частот в полосе пропускания имеют одинаковые временные задержки. Однако это характерно только для фильтра Бесселя низких частот, другие фильтры Бесселя — ПФ, ППФ, ФВЧ — таким свойством не обладают (линейность фазовой характеристики ФНЧ Бесселя не сохраняется при операциях преобразования шкалы частот для получения фильтров с другими АЧХ).
Переходная характеристика фильтра Бесселя имеет малую величину перерегулирования. Это особенно важно при работе с импульсными сигналами, которые надо передавать с минимальными искажениями. Хорошая фазовая характеристика фильтров этого типа достигается ценой ухудшения амплитудной характеристики. АЧХ не является максимально плоской в полосе пропускания и не имеет крутого спада. При этом она монотонна. Передаточные функции фильтров Бесселя содержат только полюса.
Полиномы фильтров Бесселя представлены в табл. 6.
Таблица 6
| n | N | D(s) |
| (s + 1) | ||
| (s2 + 3s + 3) | ||
| (s + 2,322)(s2 + 3,678s + 6,459) | ||
| (s2 + 5,792s+ 9,14)(s2 + 4,208s + 11,49) | ||
| (s + 3,647)(s2 + 6,704s + 14,27)(s2 + 4,649s + 18,16) | ||
| (s2 + 5,032s + 26,51)(s2 + 7,471s + 20,85)(s2 + 8,497s + 18,80) | ||
| (s + 4,972)(s2 + 5,371s + 36,60)(s2 + 8,140s + 28,94)(s2 + 9,517s + 25,67) | ||
| (s2+5,678s+48,43)(s2+8,737s+38,57)(s2+10,41s+33,93)(s2+11,18s+31,98) |
| <== предыдущая страница | | | следующая страница ==> |
| Схемы полосно-подавляющих фильтров | | | Преобразование и масштабирование |
Дата добавления: 2014-03-13; просмотров: 439; Нарушение авторских прав

Мы поможем в написании ваших работ!