МЕМБРАННЫЕ ПРОЦЕССЫ

Мембранные процессы – процессы разделения жидких и газовых смесей с использованием полупроницаемых мембран (перегородок).

Область применения мембранных процессов:

- разделения азеотропных смесей,

- очистка и концентрация растворов, растворов ВМС,

- концентрирования фруктовых и овощных соков, молока,

- очистка промышленных стоков,

- очистка воды и т.д.

Мембранные процессы малоэнергоемкы и экологический чисты.

Рассмотрим процесс мембранного разделения на примере бинарного раствора компонента В в растворителе А. Пусть растворитель проходит сквозь мембрану лучше, чем растворенное вещество. Тогда после контакта с мембраной исходная смесь разделится на два продукта: концентрат (ретант), обогащенный растворенным веществом В и фильтрат (пермеат), сменьшей концентрацией компонента В по сравнению с исходной смесью (рис.8.1).

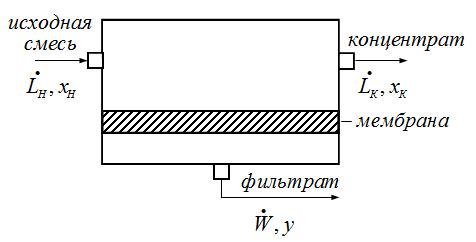
Рис.8.1. Схема процесса мембранного разделения: , , 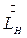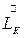- массовые расходы и 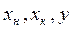массовые доли компонента В в исходной смеси, концентрате и фильтрате; , .

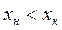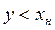Для представленной схемы процесса мембранного разделения можно записать уравнения материального баланса по смеси в целом и компоненту В соответственно:

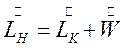(8.1)

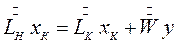(8.2)

Процесс мембранного разделения характеризуется двумя основными параметрами: селективностью j и проницаемостью j. Селективность определяется долей растворенного компонента В, не прошедшего сквозь мембрану

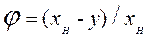(8.3)

Если мембрана совершенно не пропускает компонент В, то 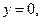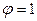- достигается полное разделение (компонент В отсутствует в фильтрате). Если же мембрана одинаковым образом пропускает оба компонента А и В, то ее селективность 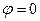, , 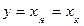разделение полностью отсутствует.

Проницаемость (удельная производительность, поток массы) – масса фильтрата 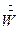, проходящая через единицу поверхности мембраны 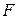за единицу времени

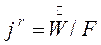, (кг/м²с) (8.4)

Дата добавления: 2014-03-22; просмотров: 492; Нарушение авторских прав

Мы поможем в написании ваших работ!