
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Метод стрельб
Основные черты этого метода рассмотрим для случая n=1 и граничных условиях вида 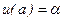 и
и 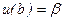 . Если отбросить второе граничное условие и выбрать некоторое значение параметра
. Если отбросить второе граничное условие и выбрать некоторое значение параметра 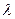 , то начальная задача превращается в задачу Коши. Численно интегрируя ее, получим решение, которое удовлетворяет первому краевому условию. В целом
, то начальная задача превращается в задачу Коши. Численно интегрируя ее, получим решение, которое удовлетворяет первому краевому условию. В целом 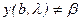 , то есть это решение не удовлетворяет второму граничному условию. Тогда, изменяя
, то есть это решение не удовлетворяет второму граничному условию. Тогда, изменяя 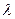 , добьемся того, что
, добьемся того, что 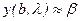 с необходимой точностью. Таким образом, задача сводится к задаче Коши и решению алгебраического уравнения. Если
с необходимой точностью. Таким образом, задача сводится к задаче Коши и решению алгебраического уравнения. Если 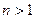 , то в качестве начальных условий для задачи Коши берут
, то в качестве начальных условий для задачи Коши берут 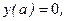
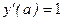 , …,
, …, 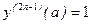 и ведут пристрелку параметра
и ведут пристрелку параметра 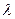 до выполнения
до выполнения 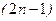 граничных условий, которые остаются.
граничных условий, которые остаются.
Этот метод трудно применять, если задача Коши плохо обусловленна, то есть когда малые изменения параметра 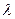 резко меняют решение
резко меняют решение 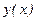 .
.

| <== предыдущая страница | | | следующая страница ==> |
| Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти | | | Фазовый метод |
Дата добавления: 2014-04-15; просмотров: 299; Нарушение авторских прав

Мы поможем в написании ваших работ!