Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА
Общая характеристика способа преобразования комплексного чертежа. Многие задачи решаются легко и просто, если прямые линии, плоские фигуры (основания, грани, ребра, оси) рассматриваемых геометрических тел находятся в частном положении. Такое частное, наивыгоднейшее взаимное расположение геометрического элемента и плоскостей проекций может быть обеспечено преобразованием чертежа.
Трудоемкость и, как следствие, точность графического решения задач часто зависит не только от сложности задачи, но и от того, какое положение занимают геометрические образы, входящие в условие задачи, по отношению к плоскостям проекций.
Для упрощения решения метрических и позиционных задач применяют различные методы преобразования ортогональных проекций. После таких преобразований новые проекции позволяют решать задачу минимальными графическими средствами.
Переход от общего положения геометрического образа к частному можно осуществить изменением взаимного положения проецируемого объекта и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями:
во-первых – перемещением в пространстве проецируемого объекта так, чтобы он занял частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве;
во-вторых – выбором новой плоскости проекций, по отношению к которой проецируемый объект, не меняющий своего положения в пространстве, окажется в частном положении.
Первый способ лежит в основе метода вращения (и как частные случаи: совмещения и плоско-параллельного перемещения); второй – составляет теоретическую базу способа замены плоскостей проекций.
Рассмотрим каждый из этих случаев в отдельности.
 |
Метод перемены плоскостей проекций. Способ замены плоскостей проекций состоит в том, что одна из плоскостей заменяется на новую. Эта плоскость выбирается перпендикулярно оставшейся плоскости проекций. Геометрический элемент при этом не меняет своего положения в пространстве. Новую плоскость располагают так, чтобы по отношению к ней геометрический элемент занимала частное положение, удобное для решения задачи.
Рис. 1.75 Рис. 1.76
Перемену плоскостей проекций можно производить несколько раз.
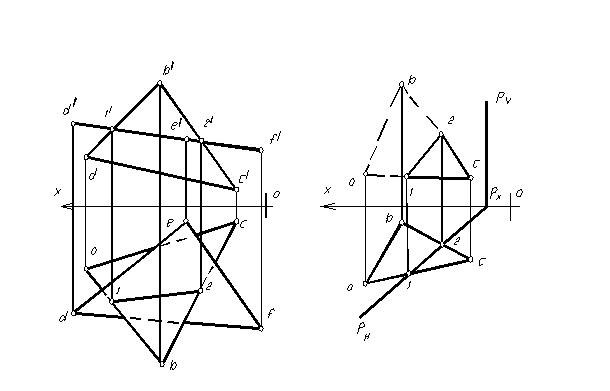
На рисунке 76 показано преобразование проекции точки А из системы HV в систему HV1 , в которой вместо фронтальной плоскости проекций введена новая вертикальная плоскость V1, а горизонтальная плоскость проекций осталась неизменной. Получаем новую систему двух взаимно перпендикулярных плоскостей H и V1. В новой системе горизонтальная проекция точки осталась неизменной. Проекция a1/ точки А на новую плоскость V1 находится от плоскости H на том же расстоянии что и проекция a / точки А на плоскости V. Это условие позволяет легко строить проекции точки на комплексном чертеже (рис. 77) на новой плоскости проекций.
 |
Используя вышеизложенное сделаем заключение: расстояние от старой проекции точки до старой оси, равно расстоянию от новой проекции точки до новой оси.
Рис. 1.77
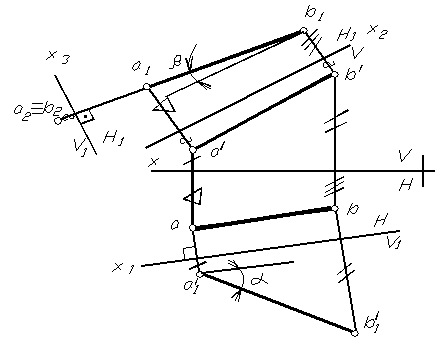
На рисунке 1.77 показано нахождение натуральной величины отрезка АВ и углов наклона его к горизонтальной и фронтальной плоскостям проекций.
При замене фронтальной плоскости проекций V на новую V1 (она вводится перпендикулярной оставшейся горизонтальной плоскости проекций H и параллельно отрезку АВ ) новая ось x1 проводится параллельно горизонтальной проекции отрезка (x1 // ab ). Используя правило ортогонального проецирования (проекционные линии связи всегда перпендикулярны оси проекций) и условие получения новой проекции точки при замене плоскостей проекций, находим новую проекцию прямой АВ – a1 / b1/
Полученная проекция по величине есть натуральная величина отрезка АВ, здесь же находится угол наклона отрезка к горизонтальной плоскости проекций.
При замене горизонтальной плоскости проекций (новая плоскость вводится параллельной отрезку в пространстве и перпендикулярно оставшейся фронтальной плоскости проекций), получаем опять-таки натуральную величину отрезка и угол наклона его к фронтальной плоскости проекций.
 |
При замене последовательно горизонтальной и фронтальной плоскостей проекции получаем в новой системе плоскостей прямую АВ в виде точки, т. е. в новой системе а прямая становится проецирующей.
Рис. 1.78
На рисунке 1.78 показано нахождение натуральной величины плоской фигуры – треугольника АВС и угол наклона его к горизонтальной плоскости проекций. Для этого фронтальная плоскость проекций заменена на новую (перпендикулярную оставшейся горизонтальной плоскости проекций и треугольнику АВС) - V1 . Из условия перпендикулярности прямой и плоскости в треугольнике проведена горизонталь и новая ось x1 проведена перпендикулярно горизонтальной проекции горизонтали ad. Тогда на новую плоскость V1 треугольник проецируется в линию и здесь же можно увидеть угол наклона треугольника к горизонтальной плоскости проекций. Далее заменив горизонтальную плоскость проекций на новую, перпендикулярную плоскости V1 и параллельную плоскости треугольника, получим в новой системе плоскостей натуральную величину треугольника АВС.
Способ вращения. При применении способа вращения плоскости проекций остаются неизменными, а изменяется положение объекта в пространстве. Изменение положения объекта достигается вращением его вокруг некоторой оси. В качестве оси вращения обычно выбирают проецирующую прямую или прямую уровня, т.к. построение, выполняемые на комплексном чертеже при вращении вокруг этих прямых, значительно проще построений при вращении вокруг прямой общего положения.
При вращении вокруг какой-либо оси следует помнить, что вращающаяся точка описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. Центр этой окружности является основанием перпендикуляра, опущенного из вращаемой точки на ось вращения, или, иначе, точкой пересечения с осью вращения плоскости, в которой вращается точка. Совершенно очевидно, что все точки объекта поворачиваются на один и тот же угол.
Т.о. При вращении точки вокруг горизонтальной (фронтальной) проецирующей прямой горизонтальная (фронтальная) проекция точки перемещается по окружности, а фронтальная (горизонтальная) проекция – прямой параллельной оси.
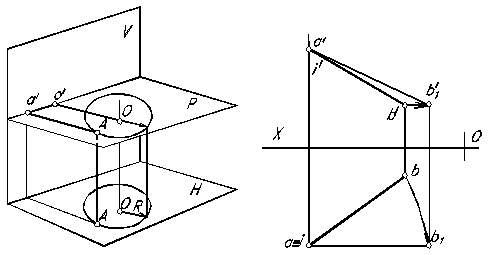
Рис. 1.79
Рассмотрим поворот отрезка прямой линии вокруг заданной оси. При этом, если ось вращения выбрать проходящей через один из концов отрезка, то построение упростится, так как точка, через которую проходит ось, будет неподвижной и для поворота отрезка надо построить новое положение проекций только одной точки – другого конца.
На рисунке 1.79 показан случай, когда для поворота отрезка АВ выбрана ось вращения, перпендикулярная к горизонтальной плоскости проекций, и проходящая через точку А. При повороте вокруг такой оси можно, например, расположить отрезок параллельно фронтальной плоскости проекций. Горизонтальная проекция отрезка в своем новом положении
параллельна оси ОХ. Найдя точку b'2 и построив отрезок a' b'2, получаем фронтальную проекцию отрезка АВ в его новом положении. Проекция a' b'2 выражает длину отрезка АВ. Угол a' b'2 b' равен углу между прямой АВ и горизонтальной плоскостью проекций.
1.17Многогранники
Гранной поверхностью называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. Гранные поверхности можно подразделить на два вида: пирамидальные и призматические.
Часть пространства, ограниченная со всех сторон поверхностью, называется телом.
Многогранником называется тело, ограниченное плоскими многоугольниками. Рассмотрение многогранников ограничим рассмотрением призм и пирамид.
Призмой называется многогранник, у которого одинаковые взаимно параллельные грани – основания, а остальные – боковые грани – параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой. Для задания призмы достаточно задать одно ее основание и боковое ребро.
Пирамида представляет собой многогранник, у которого одна грань – произвольный многоугольник, принимающейся за основание, а остальные грани (боковые) – треугольники с общей вершиной, называемой вершиной пирамиды.
Сечение многогранников плоскостью. В сечении гранных поверхностей плоскостями получаются многоугольники, вершины которых определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью.
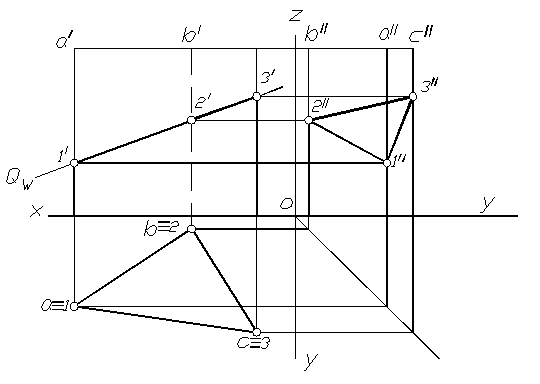
Рис. 1.80
Многоугольник сечения может быть найден двумя путями:
- вершины многоугольника находятся как точки пересечения прямых (ребер) с секущей плоскостью;
- стороны многоугольника находятся как линии пересечения плоскостей (граней) многогранника с секущей плоскостью.
В качестве примера построим сечение призмы фронтально-проецирующей плоскостью Q (рис. 1.80) .
Секущая плоскость перпендикулярно фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом Qvплоскости Q. Таким образом, фронтальная проекция фигуры сечения 1/2/3/
Определяется при пересечении фронтальных проекций ребер призмы со следом Qv. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы. Профильная проекция фигуры сечения находится по принадлежностям проекций точек 1,2,3 соответствующим ребрам призмы. Если считать что плоскость Qотсекает верх призмы, то фигура сечения на профильной плоскости видна, а если нет, то линия 2//3// изобразится невидимой.
На рисунке 1.81 показано сечение четырехугольной пирамиды фронтально-проецирующей плоскостью Q.
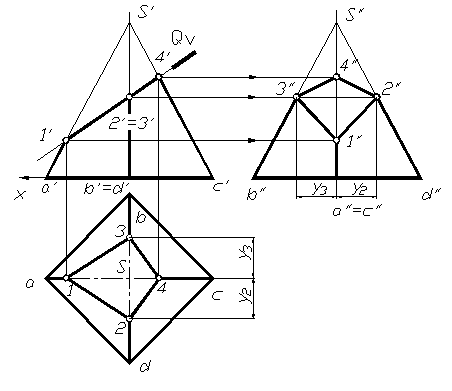
Рис. 1.81
Секущая плоскость перпендикулярна фронтальной плоскости проекций, следовательно, все линии, лежащие в этой плоскости, в том числе и фигура сечения на фронтальной проекции, совпадут с фронтальным следом плоскости. Таким образом, фронтальная проекция фигуры сечения 1,2,3,4 определится при пересечении фронтальных проекций ребер пирамиды со следом плоскости. Горизонтальные проекции этих точек находим, проводя проекционные линии связи на горизонтальную проекцию соответствующих ребер. Если считать что плоскость Q отсекает верх пирамиды, то на фронтальной плоскости фигура сечения видна, если нет, то 3//4//, 4//2//будут невидимы.
Призма с вырезом. В качестве примера построения сечения многогранника несколькими плоскостями рассмотрим построение призмы с вырезом, образованным треугольной призмой.
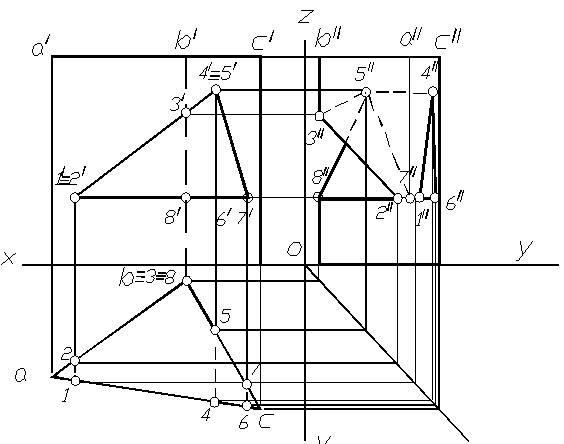 |
Рис. 1.82
На фронтальной проекции отмечаем проекции точек встречи ребра B заданной призмы с гранями призмы выреза: 3/и 8/, и точки пересечения ребер призмы выреза с гранями заданного тела: 1/2/4/5/6/7/. Находим горизонтальные проекции отмеченных точек. Все они находятся на горизонтальной проекции заданной призмы. По двум полученным проекциям точек находим их профильные проекции. С учетом видимости соединяем точки, принадлежащие соответствующим граням заданной призмы. В грани AB: точки 3,2,8, в грани BC: точки 3,5,7,8 и в грани AC: 1,4,6,1.
Пирамида с вырезом. На рисунке 1.83 показано построение пирамиды с вырезом (как результат сечения пирамиды несколькими проецирующими плоскостями, образовавшими призматический вырез). Обозначаем на фронтальной проекции точки, одновременно принадлежащие заданной пирамиде и призматическому вырезу. По принадлежности точек ребрам заданной пирамиды находим их горизонтальные и профильные проекции. Точки (3) пересечения ребра призматического выреза с гранями заданной пирамиды можно найти двумя способами. Первый способ заключается в проведении через точки выреза плоскости S параллельной основанию (след которой обозначается на комплексном чертеже). В сечении пирамиды этой плоскостью образуется треугольник подобный основанию, проходящий через точку K. Данному треугольнику принадлежат точки 3,1,6,7,5,4,3. Можно также найти точки на поверхности пирамиды проведением через них прямых, связывающих их с вершиной пирамиды и дальнейшим построением проведенных прямых на горизонтальной плоскости проекций и нахождением на них искомых точек. Полученные точки соединяют с учетом видимости в необходимой последовательности по соответствующим граням заданной пирамиды (чтобы две точки принадлежали одной секущей плоскости и одной грани пирамиды).
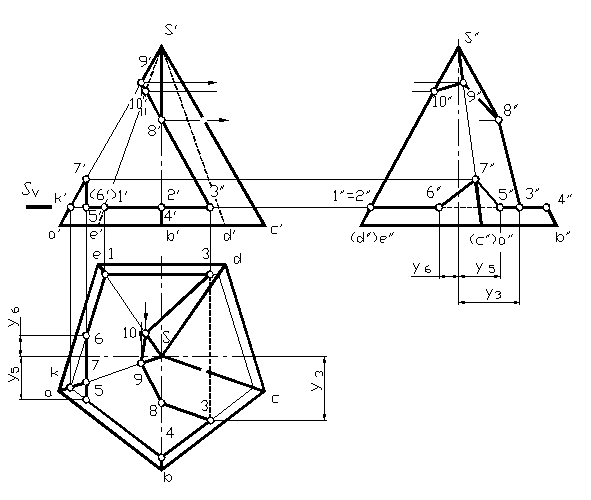
Рис. 1.83
1.18 Тела вращения
Рассмотрим некоторые из многочисленных поверхностей вращения.
Поверхности, образованные вращением прямой линии. К таковым относятся цилиндр и конус.
Цилиндр вращения – поверхность, полученная вращением прямой вокруг параллельной ей оси и ограниченная двумя взаимно параллельными плоскостями.
Конус вращения – поверхность, образованная вращением прямой (образующая) вокруг пересекающейся с ней осью (направляющая).
Примером поверхностей, образованных вращением окружности вокруг неподвижной оси является сфера.
Сфера – поверхность, полученная вращением окружности вокруг ее диаметра.
Сечение цилиндра плоскостью. При сечении цилиндра вращения плоскостью, параллельной оси вращения, в сечении получается пара прямых (образующих). Если секущая плоскость перпендикулярна к оси вращения, в сечении получается окружность. В общем случае, когда секущая плоскость наклонена к оси вращения цилиндра, в сечении получается эллипс.
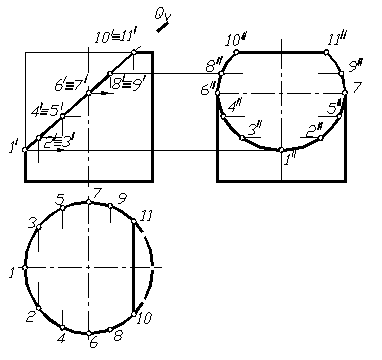
Рис. 1.84
На рисунке 1.84 показан пример построения проекций линии сечения цилиндра фронтально проецирующей плоскостью Q, когда в сечении получается эллипс.
Фронтальная проекция фигуры сечения в этом случае совпадает с фронтальным следом плоскости, а горизонтальная – с горизонтальной проекцией поверхности цилиндра – окружностью. Профильная проекция строится по двум имеющимся проекциям – горизонтальной и фронтальной, замеряя игрековые координаты точек относительно оси цилиндра и откладывая их на проекционных линиях связи соответствующих точек.
Сечение конуса плоскостью. В зависимости от положения секущей плоскости в сечении конуса вращения могут получиться различные линии, называемые линиями конических сечений.
Если секущая плоскость проходит через вершину конуса перпендикулярно его основанию, то в сечении получается пара прямых – образующих (треугольник – рис. 1.85а). В результате пересечения конуса плоскостью, перпендикулярной к оси конуса, получается окружность (рис. 185б). Если секущая плоскость наклонена к оси вращения конуса и не проходит через ее вершину, в сечении конуса могут получиться эллипс (секущая плоскость пересекает все образующие конуса – рис. 1.85в). Парабола образуется, если секущая плоскость параллельна одной из образующих конуса (рис. 1.85г). Гипербола образуется в случае, если секущая плоскость параллельна двум образующим конуса в зависимости от угла наклона секущей плоскости к основанию конуса (рис. 1.85д).
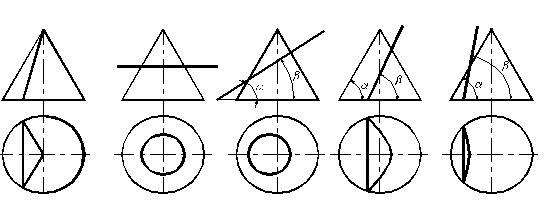
а б в г д
Рис. 1.85
Известно, что точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности. Для конуса графически наиболее простыми линиями являются образующие и окружности. Следовательно, если по условию задачи требуется найти горизонтальные проекции точек, принадлежащих поверхности конуса, то нужно через точки провести одну из этих линий.
На рисунке 1.86 дан пример построения проекций линии сечения конуса фронтально проецирующей плоскостью, когда в сечении получается эллипс.
Фигура сечения на фронтально плоскости совпадает со следом секущей плоскости. Обозначим характерные точки (точки, принадлежащие фронтальному очерку конуса – 1, 6 и 4, 5 – точки, принадлежащие профильному очерку конуса) и несколько промежуточных (чем больше будет отмечено таких точек, тем точнее получится фигура сечения – эллипс). Горизонтальные и профильные проекции точек 1,4,5,6, находятся без дополнительных построений, так как они принадлежат соответствующим очеркам конуса. Для точек 4 и 5 находятся их профильные проекции из условия принадлежности их профильному очерку конуса, а затем, измерив игрековую координату этих точек от оси конуса, отмечаются их горизонтальные проекции. Для нахождения проекций промежуточных точек можно воспользоваться методом проведения секущих плоскостей, параллельных основанию конуса или проведением через отмеченные точки образующих конуса с последующим нахождением горизонтальных проекций этих образующих и нахождением на них соответствующих точек. Далее по двум полученным проекциям строятся третью проекции отмеченных точек. Полученные проекции точек соединяются плавной кривой с учетом видимости (на примере верхняя часть конуса отсечена плоскостью Q и поэтому вся фигура сечения на профильной плоскости видна). Если такого отсечения не происходит, то на профильной проекции часть кривой сечения 465 изобразится невидимой линией.
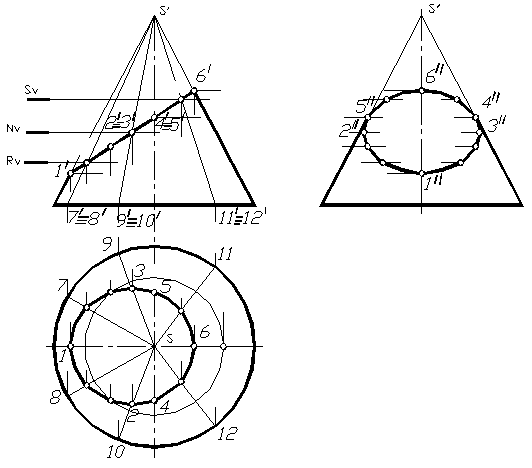
Рис. 1.86
Конус с вырезом. На рисунке 1.87 показан конус, в котором выполнен вырез, образованный тремя плоскостями частного положения, образующих призматический вырез. Фронтальная проекция фигуры сечения совпадает с очерком призматического выреза. Для нахождения горизонтально и профильной проекций выреза отмечаем ряд необходимых точек. Необходимо отметить характерные точки, принадлежащие очеркам конуса, точки перегиба плоскостей выреза и ряд промежуточных для точности построения определенных кривых.
В данном случае отмечаются точки 5,6 и 11,12 , принадлежащие профильному очерку конуса; точки 1, 2, 3, 4, 9,10, являющиеся ребрами (линии перегиба плоскостей выреза) призматического выреза. Для более точного построения части параболы необходимо отметить ряд точек (чем их будет больше, тем точнее получится кривая) находящихся между точками 3, 9 и 4, 10 (в данном случае это точки 7 и 8). Для построения части выреза, в результате которого образуется часть гиперболы, отмечаются точки, находящиеся между точками 1 и 3, 2 и 4 (в данном случае это точки 13 и 14). Их также необходимо взять достаточное количество.
Построив горизонтальные и профильные проекции отмеченных точек, фигуры проекций выреза соединяются с учетом видимости. На горизонтальной плоскости линии входа и выхода призматического выреза конуса видны. На профильной проекции видимость определяется по граничным точкам 5, 6 и 11, 12. Линия 5, 7, 9, 11 и 6, 8, 10, 12 на профильной проекции не видна, но, учитывая форму выреза, куски линии 5, 7 и 6, 8 до линий 3, 13 и 4, 14 будут видны.
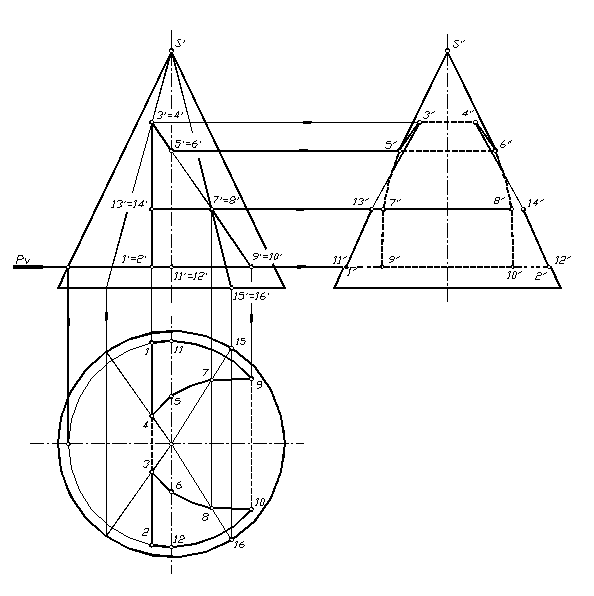
Рис. 1.87
Сечение шара плоскостью. Если шар пересекать плоскостью, то в сечении всегда получается окружность. Эта окружность может проецироваться:
- в прямую, если секущаяплоскость перпендикулярна к плоскости проекций;
- в окружность с радиусом, равным расстоянию от оси вращения шара до очерка, если секущая плоскость параллельна какой-либо плоскости проекций;
- в эллипс, если секущая плоскость не параллельна ни одной из плоскостей проекций.
Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную какой-либо плоскости проекций, и построить окружность, на которой находится эта точка
На рисунке 1.88 показано построение проекций линии сечения шара фронтально проецирующей плоскость.
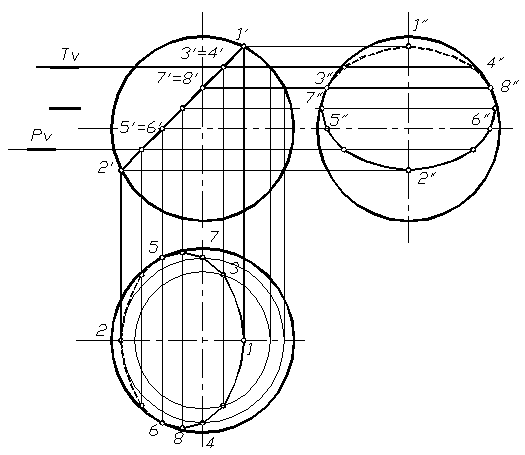
Рис. 1.88
Построение начинаем с определения характерных точек. Точки 1 и 2 находятся на фронтальном очерке шара (главном меридиане). Эти точки – концы малой оси эллипса, а также самая высокая и самая низкая точки. Их горизонтальные и профильные проекции находятся на соответствующих окружностях шара, которые на горизонтальной и профильной плоскостях совпадают с осями. Точки 7 и 8 находятся на профильном очерке шара (профильном меридиане) и служат для определения видимости на профильной плоскости проекций. Горизонтальные проекции этих точек находятся по фронтальным и профильным. Точки 5 и 6 находятся на горизонтальном очерке шара (экваторе) и служат для определения видимости на горизонтальной плоскости проекций. Профильные проекции этих точек находим по горизонтальным и фронтальным проекциям. Для точного построения линии сечения необходимо найти несколько дополнительных точек. Для их построения используются вспомогательные секущие плоскости (например, плоскости горизонтального уровня T и P), которые в сечении дают окружность на горизонтальной плоскости. Полученные точки соединяют плавной кривой с учетом их видимости.
Шар с вырезом. На рисунке 1.89 показано построение проекций шара с вырезом, образованным тремя плоскостями частного положения, образующими призматический вырез.
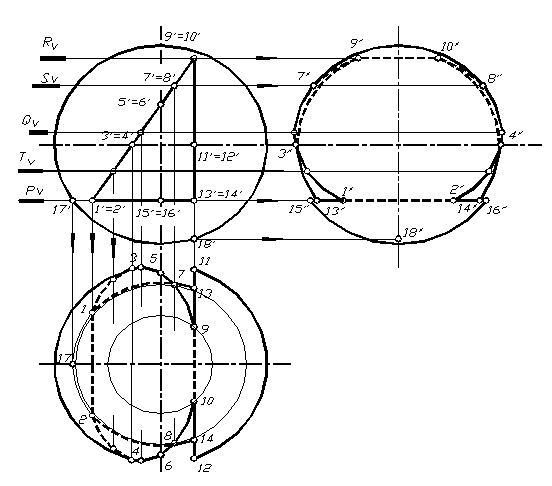
Рис. 1.89
Для построения проекций выреза отмечаем необходимые точки. Это точки, принадлежащие очеркам шара, точки перегиба плоскостей выреза, а также ряд промежуточных для более точного построения линий выреза.
Нахождение проекций характерных точек, принадлежащие очеркам шара, выполняется без дополнительных построений из учета принадлежности их определенным очеркам шара (точки 3, 4 и 11, 12 находятся на горизонтальном очерке шара, точки 7, 8 и 15, 16 – на профильном очерке). Проекции всех остальных точек находятся путем проведения через них дополнительных плоскостей уровня (горизонтального – как на данном примере или профильного). Например, при сечении шара плоскостью горизонтального уровня Р в сечении образуется окружность соответствующего радиуса. Горизонтальные проекции точек 1,2,15,16,13,14 находятся на горизонтальной проекции полученной окружности. Профильные проекции этих точек находятся по двум уже построенным фронтальным и горизонтальным. Кусочки линии сечения от этой плоскости с одной стороны шара: 1,15,13 и с другой – 2,16,14. Куски линии сечения шара в пределах выреза от плоскости, находящееся меду точками 1, 9 и 2, 10 с одной стороны шара: 1,3,5,7,9 и с другой – 2,4,6,8,10. Между точками 9, 13 и 10, 14 образуется часть окружности соответствующего радиуса, которая на горизонтальную плоскость проецируется в линию, а на профильную в окружность.
Полученные части линий проекций выреза соединяем с учетом видимости на горизонтальной и профильных плоскостях. Границей видимости на горизонтальной плоскости служат точки 3, 4 и 11, 12: на профильной плоскости – точки 5, 6 и 15, 16.
Литература
1. Бубенников А.В., Громов М.Я. Начертательная геометрия. М.: Высшая школа, 1973. – 243с., ил.
2. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии: Учеб. Пособие/Под ред. Ю.Б. Иванова. – 23 изд., перераб.–М.: Наука. Гл. ред. физ. мат. лит., 1988. – 272 с., ил.
3. Фролов С.А. Начертательная геометрия: Учеб. для вузов. – 2-е изд.,перераб. и доп. - М.: Машиностроение, 1983. – 240 с., ил.
4. Чекмарев А.А. Инженерная графика: Учеб. для машиностроит. спец. вузов. – 2-е изд., испр. – М.: Высш. Шк., 1998. – 365 с., ил.
|
| <== предыдущая страница | | | следующая страница ==> |
| Взаимное положение прямой и плоскости, двух плоскостей | | | ПЕРЕДМОВА |
Дата добавления: 2014-04-16; просмотров: 3526; Нарушение авторских прав

Мы поможем в написании ваших работ!