Построение интервальных вариационных рядов

Покажем методику построения интервальных вариационных рядов распределения на следующем примере.

Пример 3.3.В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):

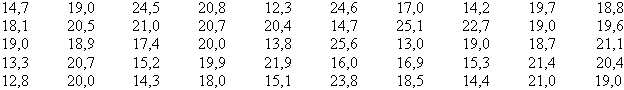
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения.

1) Определим число интервалов.

Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса

n = 1 + 3,322lgN

где n – число интервалов;

N – объем совокупности (число единиц наблюдения).

Для нашего примера получим: n = 1 + 3,322lgN = 1 + 3,322lg50 = 6,6 » 7.

2) Определим величину интервалов(i) по формуле

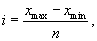
где х_max – максимальное значение признака;

х_min – минимальное значение признака.

Для нашего примера

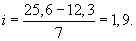
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0.

3) Определим границы интервалов.

Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0-14,0; 14,0-16,0; 16,0-18,0; 18,0-20,0; 20,0-22,0; 22,0-24,0; 24,0-26,0.

Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18-25, 26-33, 34-41, 42-49, 50-57, 58-65, 66 и более.

Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т. е. записать: до 14,0; 24,0 и выше.

4) По исходным данным построимранжированный ряд. Для этого запишем в порядке возрастания значения, которые принимает признак. Результаты представим в таблице:

Ранжированный ряд величин процентной ставки коммерческих банков*

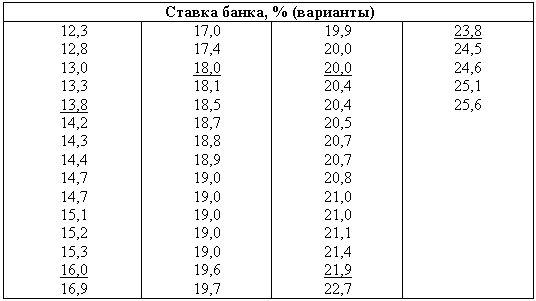
* В таблице чертой отделены значения признаков, попадающих в один и тот же интервал.

5. Подсчитаем частоты.

При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей[1]. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу.

Результаты группировки, полученные в нашем примере, оформим в таблице.

Распределение коммерческих банков по величине кредитной ставки

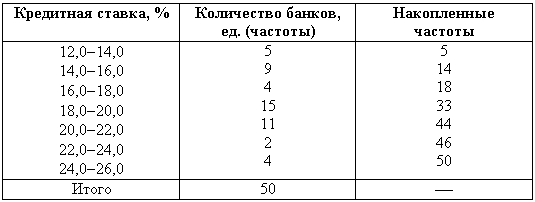
В последней графе таблицы представлены накопленные частоты, которые получают путем последовательного суммирования частот, начиная с первой (например, для первого интервала – 5, для второго интервала 5 + 9 = 14, для третьего интервала 5 + 9 + 4 = 18 и т. д.). Накопленная частота, например, 33, показывает, что у 33 банков кредитная ставка не превышает 20% (верхняя граница соответствующего интервала).

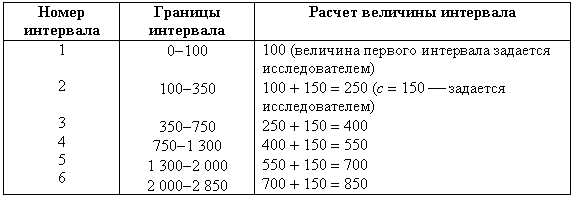
В процессе группировки данных при построении вариационных рядов иногда используются неравные интервалы. Это относится к тем случаям, когда значения признака подчиняются правилу арифметической или геометрической прогрессии или когда применение формулы Стерджесса приводит к появлению «пустых» интервальных групп, не содержащих ни одной единицы наблюдения. Тогда границы интервалов задаются произвольно самим исследователем исходя из здравого смысла и целей обследования либо по формулам. Так, для данных, изменяющихся в арифметической прогрессии, величина интервалов вычисляется следующим образом:

i_k = i_{k - 1} + c,

где i_k - величина вычисляемого интервала;

i_{k - 1} - величина предыдущего интервала;

с - константа, на которую происходит увеличение длин интервалов.

Порядок расчетов границ неравных интервалов для данных, изменяющихся приблизительно в арифметической прогрессии, показан в табл. 3.8.

Таблица 3.8 – Схема интервального вариационного ряда с неравными интервалами для данных, подчиняющихся правилу арифметической прогрессии

Для показателей, приблизительно изменяющихся в геометрической прогрессии, величину интервалов можно вычислить по формуле

i_k = i_{k - 1} × c,

где i_k – величина вычисляемого интервала;

i_{k - 1} – величина предыдущего интервала;

с – константа-множитель геометрической прогрессии

Глава 5. Абсолютные и относительные величины в статистике

Дата добавления: 2014-04-24; просмотров: 2150; Нарушение авторских прав

Мы поможем в написании ваших работ!