ОБЩИЕ ПРИНЦИПЫ РАСЧЕТА ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИНСТРУМЕНТА

а	б
Рис. 5.1. Главный угол в плане токарного резца при обработке цилиндрической (а) и конической (б) поверхностей

5.1. Единая геометрия режущего лезвия

При разработке рабочего чертежа инструмента конструктор задает в ортогональной системе плоскостей проекции углы режущего лезвия (или лезвий), выполняемые при изготовлении инструмента. Некоторые из этих углов остаются постоянными в процессе эксплуатации инструмента, а другие могут претерпевать изменения. Например, главный угол в плане j проходного токарного резца, как видно из рис. 5.1, зависит от того, цилиндрический или конический участок заготовки обрабатывается этим резцом. Если вершина резца установлена выше или ниже оси вращения заготовки, то от изначально заданных будут отличаться значения практически всех углов режущего лезвия.

Чтобы рассчитать и проанализировать углы лезвия, возникающие при работе инструмента, необходимо точно определить взаимное расположение инструмента и заготовки в процессе резания. Для этого служат шесть воображаемых плоскостей, а именно:

– основная плоскость;

– плоскость резания;

– главная секущая плоскость;

– радиальная секущая плоскость;

– осевая секущая плоскость;

– нормальная секущая плоскость.

Основную плоскость P_v проводят через выбранную точку M активного участка главной режущей кромки инструмента перпендикулярно вектору скорости главного движения в этой точке.

Плоскость резания P_n проводят касательно к главной режущей кромке в данной ее точке и перпендикулярно основной плоскости.

Главную секущую плоскость P_τ проводят через точку M по нормали к проекции главной режущей кромки на основную плоскость (рис. 5.2, а).

Радиальную секущую плоскость P_r проводят через точку M перпендикулярно фактически существующему или возможному направлению движения продольной подачи D_s, а осевую секущую плоскость P_s – перпендикулярно основной плоскости и параллельно направлению D_s (рис. 5.2, б).

Нормальную секущую плоскость P_λ проводят перпендикулярно главной режущей кромке в данной ее точке. Подробнее о различии плоскостей P_τ и P_λ будет сказано ниже.

Рис. 5.2. Система плоскостей при резании

В основной плоскостиопределяют углы лезвия в плане.

Главный угол в плане j – это наименьший угол между касательной к проекции главной режущей кромки на основную плоскость в данной точке кромки и вектором скорости подачи инструмента v_s.

Вспомогательный угол в плане j₁ – это наименьший угол между касательной к проекции вспомогательной кромки на основную плоскость в данной точке кромки и вектором v_s.

Углы в плане могут принимать только положительные значения.

В плоскости резанияопределяют угол наклона главной режущей кромки лезвия.

Угол наклона главной режущей кромки l – это наименьший угол между главной режущей кромкой и основной плоскостью. Угол lсчитают положительным, если главная режущая кромка располагается выше основной плоскости, проведенной через вершину лезвия.

В главной секущей плоскостиопределяют передний и задний углы лезвия, влияющие на динамику процесса резания.

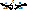
Рис. 5.3. Определение знака переднего угла лезвия

Передний угол g – это наименьший угол между плоскостью, касательной к передней поверхности инструмента в выбранной точке главной режущей кромки, и основной плоскостью. Угол g считают положительным, если в данной точке кромки для совмещения касательной плоскости с основной касательную плоскость необходимо повернуть на острый угол против хода часовой стрелки (рис. 5.3).

Главный задний угол a – это наименьший угол между плоскостью, касательной к главной задней поверхности инструмента в выбранной точке главной режущей кромки, и плоскостью резания. Задний угол может принимать только положительные значения.

Из шести плоскостей, определяющих взаимное расположение инструмента и заготовки в процессе резания, две (P_s и P_r) совпадают с плоскостями ортогональной системы, в которой выполняется чертеж инструмента. Передние g_s, g_r и задние a_s, a_r углы в этих плоскостях, как правило, совпадают с углами, заданными конструктором инструмента, и остаются неизменными при различных схемах наладки инструмента.

Рис. 5.4. К выводу формул взаимосвязи передних углов режущего лезвия

Для того, чтобы получить зависимости между углами в главной, осевой и радиальной секущих плоскостях, рассмотрим рис. 5.4, на котором в качестве примера изображено режущее лезвие с передним углом g > 0 и углом наклона главной кромки l> 0.

Пусть CЕ – проекция участка главной режущей кромки на основную плоскость P_v. Проведем через некоторую точку М этого участка главную, осевую и радиальную секущую плоскости (следы этих плоскостей на рис. 5.4 обозначены P_τ, P_s и P_r) и построим сечения режущего клина этими плоскостями.

Выберем на передней поверхности лезвия некоторую точку N, принадлежащую плоскости P_τ, и проведем через нее плоскость, параллельную плоскости резания P_n. След P_n1 этой плоскости пересечет следы плоскостей P_s и P_r в точках А и В соответственно.

Пусть расстояние между точками М и N, измеренное в основной плоскости, равно l. Тогда, поскольку в рассматриваемом примере режущее лезвие имеет положительный передний угол, точка N будет находиться ниже точки М на некоторую величину

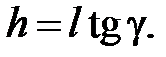(5.1)

При нулевом угле наклона главной режущей кромки точки А, В и N находились бы на одинаковом расстоянии от основной плоскости. В нашем случае главная режущая кромка (а, следовательно, и параллельная ей прямая АВ) наклонена по отношению к основной плоскости на угол l > 0, поэтому точка А лежит ниже, а точка В – выше точки N. При этом точка А находится ниже точки N на столько же, насколько точка C режущей кромки лежит ниже точки М, т.е. на

(5.2)

Соответственно точка В лежит выше точки N на столько же, насколько точка Е кромки превышает точку М, т.е. на

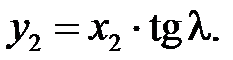(5.3)

Таким образом, точка А находится ниже точки М на h_s = h + y₁, а точка В ниже точки М на h_r = h – y₂. Тогда, как видно из рис. 5.4,

(5.4)

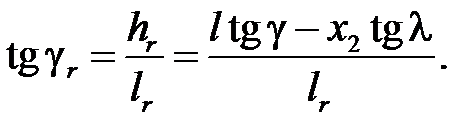(5.5)

Из треугольника АMN, в котором Ð МАN = j, получаем

(5.6)

а из треугольника ВMN, в котором Ð ВМN = j,

(5.7)

С учетом (5.6) и (5.7) выражения (5.4) и (5.5) принимают вид

; (5.8)

. (5.9)

Умножая (5.8) на sinj, а (5.9) на cosj и складывая полученные выражения, находим, что

. (5.10)

Путем столь же несложных математических преобразований из (5.8) и (5.9) можем получить зависимость для определения угла наклона главной режущей кромки, если на чертеже инструмента проставлены углы g_s и g_r:

. (5.11)

Из рис. 5.4 видно, что нормальная секущая плоскость P_λ совпадает с главной секущей плоскостью P_τ только при l= 0. В остальных случаях эти плоскости имеют различное положение в пространстве. При этом, однако, всегда соблюдается соотношение

. (5.12)

Чтобы получить зависимости между главными задними углами в различных плоскостях, выберем на задней поверхности лезвия некоторую точку Q, принадлежащую осевой секущей плоскости P_s и находящуюся на q_s ниже точки М (рис. 5.5). Проведем через точку Q плоскость, параллельную плоскости резания P_n. След P_n2 этой плоскости пересечет след плоскости P_τ в точке G, расположенной ниже точки М на .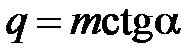

Рис. 5.5. К выводу формул взаимосвязи задних углов режущего лезвия

При нулевом угле наклона главной режущей кромки точки G и Q находились бы на одинаковом расстоянии от основной плоскости. Однако из-за того, что главная режущая кромка наклонена по отношению к плоскости P_v на угол l > 0, точка Q лежит ниже точки G на столько же, насколько точка F режущей кромки лежит ниже точки М, т.е. на

.

Раз точка Q находится ниже М на q_s = q + y, то

.

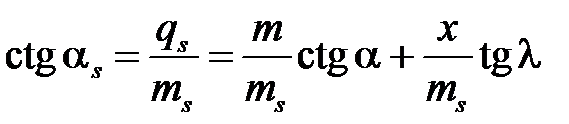Как видно из треугольника GMQ, в котором Ð МQG = j,

.

Тогда

. (5.13)

Если ввести угол h, отвечающий условию , то после несложных тригонометрических преобразований можно привести (5.13) к виду

. (5.14)

Выбрав точку Н, принадлежащую задней поверхности лезвия и плоскости P_r (см. рис. 5.5), и рассуждая по аналогии с изложенным выше, получаем

(5.15)

или

. (5.16)

Формулы (5.8)÷(5.12) и (5.13)÷(5.16), отражающие взаимосвязь между углами режущего лезвия, измеренными в различных плоскостях, часто называют формулами единой геометрии инструмента, поскольку, как будет показано далее, они применимы для анализа геометрических параметров всех режущих инструментов – от простых (например, токарного резца) до сложных (например, зуборезного долбяка).

Дата добавления: 2014-05-20; просмотров: 425; Нарушение авторских прав

Мы поможем в написании ваших работ!