Организация вычислительного процесса в универсальных программах анализа на макроуровне

На рисунке 15.3представлена граф–схема вычислительного процесса при анализе во временной области на макроуровне.

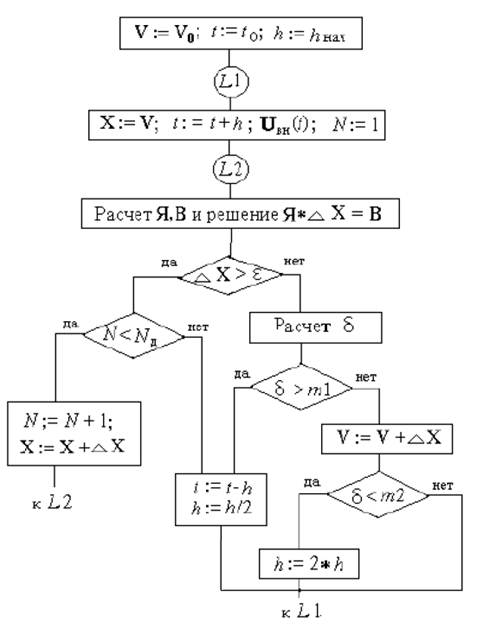
Рис.15.3. Граф–схема вычислительного процесса анализа на макроуровне:

V0(t0) – начальные условия; h и hнач – шаг интегрирования и его начальное значение; Uвн(t) – вектор внешних воздействий; N и Nд – число ньютоновских итераций и его максимально допустимое значение;ε – предельно допустимая погрешность решения СНАУ;δ – погрешность, допущенная на одном шаге интегрирования; m1 – максимально допустимое значение погрешности интегрирования на одном шаге; m2 – нижняя граница коридора рациональных погрешностей интегрирования.

Алгоритм отражает решение системы алгебро–дифференциальных уравнений

φ(dV/dt, V, t) = 0.

На каждом шаге численного интегрирования решается система нелинейных алгебраических уравнений

F(X) = 0

методом Ньютона. На каждой итерации выполняется решение системы линейных алгебраических уравнений

Я ΔX = B.

Из рисунка ясно, что при N ≥Nд фиксируется несходимость ньютоновских итераций и после дробления шага происходит возврат к интегрированию при тех же начальных для данного шага условиях. При сходимости рассчитывается δ и в зависимости от того, выходит погрешность за пределы диапазона [m2, m1] или нет шаг изменяется либо сохраняет свое прежнее значение. Параметры Nд, m1, m2, ε, hнач задаются "по умолчанию" и могут настраиваться пользователем. Матрицу Якоби Я и вектор правых частей В необходимо рассчитывать по программе, составляемой для каждого нового исследуемого объекта. Составление программы выполняет компилятор, входящий в состав программного комплекса анализа. Общая структура такого комплекса представлена на рис.15.4.

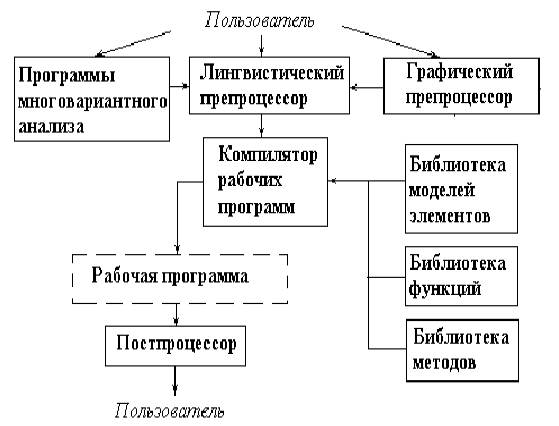
Рис.15.4. Структура программного комплекса анализа на макроуровне

Исходные данные об объекте можно задавать в графическом виде (в виде эквивалентной схемы) или на входном языке программы анализа. Запись на таком языке обычно представляет собой список компонентов анализируемого объекта с указанием их взаимосвязей. Вводимые данные преобразуются во внутреннее представление с помощью графического и лингвистического препроцессоров, в которых предусмотрена также диагностика нарушений формальных языковых правил. Графическое представление более удобно, особенно для малоопытных пользователей.

Задав описание объекта, пользователь может приступить к многовариантному анализу либо по одной из программ такого анализа, либо в интерактивном режиме, изменяя условия моделирования между вариантами с помощью лингвистического препроцессора.

Наиболее сложная часть комплекса – компилятор рабочих программ, именно в нем создаются программы расчета матрицы Якоби Я и вектора правых частей фигурирующих в вычислительном процессе.

Собственно рабочая программа – это и есть программа процесса, показанного на рис. 15.4. Для каждого нового моделируемого объекта составляются свои рабочие программы. При компиляции используются заранее разработанные математические модели типовых компонентов, известные функции для отображения входных воздействий и т.п. из соответствующих библиотек.

Постпроцессор представляет результаты анализа в табличной и графической формах, это могут быть зависимости фазовых переменных от времени, значения выходных параметров–функционалов и т.п.

Дата добавления: 2014-02-26; просмотров: 615; Нарушение авторских прав

Мы поможем в написании ваших работ!