VII. Организация рекламной кампании

Модель рекламной кампании основывается на следующих основных предположениях.

Прибыль от продаж должна покрывать издержки на рекламную кампанию. Динамика роста прибыли: вначале расходы превышают прибыль, поскольку лишь малая часть покупателей информировании о новом товаре, по мере информированности покупателей прибыль растет, по мере насыщения рынка рост прибыли падает, и наступает момент, когда рекламирование товара становится бессмысленным. При таком подходе формализуется идея насыщения, описанная в примере 3.

Примем N (t) – число информированных покупателей.

dN/dt – скорость изменения числа покупателей со временем t (t - время от начала рекламной кампании) – пропорциональна числу покупателей, еще не знающем о товаре – величине a₁(t) (N₀ – N(t)), где a₁(t) > 0 характеризует интенсивность рекламной кампании (определяется затратами на рекламу в данный момент), N₀ – общее число потенциальных покупателей.

Предполагается, что информированные потребители участвуют каким-то образом в рекламировании товара. Их вклад равен величине a₂(t) N(t) (N₀ – N(t)), который тем больше, чем больше информированных покупателей. Величина a₂(t)характеризует степень общения покупателей между собой (может быть определена опросами).

В итоге получим уравнение

dN (t) / dt = [а₁(t) + а₂(t) N (t)] (N₀ – N(t)). (7)

При а₁(t) >> а₂(t)N(t) получается модель типа (1) – Мальтуса, при противоположном неравенстве – типа (3):

dN (t) / dτ = N (N₀ – N), dτ = а₂(t) d t.

Полученная аналогия понятна, так как использовалась одна и та же идея «насыщения»: скорость роста какой-либо величины пропорциональна произведению текущего значения этой величины N (t) на разность N₀ – N (t) между ее равновесным (популяция) либо предельным (покупатели) и текущим значениями.

В зависимости от значений величин а₁(t), а₂(t), N(t) могут разрабатываться мероприятия на улучшение результатов прямой рекламы (параметр а₁(t)) и косвенной рекламы (параметр а₂(t)).

Если рассмотреть модель (7) в окрестности точки N(t =0) = N(0) = 0 (t =0 – момент начала кампании), считая, что N<< N₀, а₂(t)N(t) << а₁(t), то уравнение (7) примет вид

dN (t) / d t = а₂(t) N₀

и имеет решение

N(t) = N_{0 ,}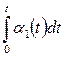

удовлетворяющее естественному начальному условию при t =0.

Из последнего уравнения можно вывести соотношение между рекламными издержками и прибылью в начале кампании.

Обозначим: р – прибыль от единичной продажи, s - стоимость элементарного акта рекламы (расклейка афиш).

Тогда суммарная прибыль Р = р N(t) = р N_{0 ,}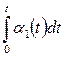

Произведенные затраты S = s .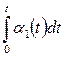

Прибыль превосходит издержки при условии р N₀ > s (в реальности между всеми этими значениями имеются временные задержки, что может быть учтено в более полных моделях.

Условие р N₀ > s (прибыльность рекламы) справедливо при малых значениях функции N(t), когда функции Р и S растут со временем по одинаковым законам.

При увеличении N(t) усиливается действие косвенной рекламы. Этот нелинейный эффект в изменении величины при неизменном темпе роста издержек даст возможность скомпенсировать финансовые потери начальной стадии кампании.

Рассмотрим частный случай: коэффициенты а₁ и а₂ примем постоянными. Тогда в (7) можно принять а₁/а₂ + N = N*.

В случае такой замены оно сводится к известному логистическому уравнению

dN* (t) / d t = а₂N* (N₀* – N*), N₀* = а₁/а₂ + N₀, (7*)

имеющему решение

N* (t) = N₀* [1 + (N*₀ а₂/а₁ -1)exp (-N₀* а₂ t)]^-1.

При этом N*(0) = а₁/а₂, так что N*(0) = 0 и начальное условие выполняется. Из предыдущего уравнения (7*) максимум производной достигается при N* = N₀*/2, N = (а₁/а₂ + N₀)/2:

(dN*/dt)_m = (dN/dt)_m = а₂ N₀*² / 4 = а₂(а₁/а₂ + N₀)²/4.

В этот период текущая, получаемая в единицу времени прибыль

Р_m = p (dN/dt) = p а₂(а₁/а₂ + N₀)²/4.

Вычитая из Р_m начальную текущую прибыль Р₀ = p (dN/dt)_t=0 = а₁ N₀, получим

Р_m – Р₀ = p/4 (а₁/а₂^-1/2 - а₂^-1/2 N₀)².

Необходимое условие суммарного экономического эффекта от кампании (Р_m > а₁s) определяются всем ее ходом, характеристики которого вычисляются из полученных уравнений.

Как следует из (7*), начиная с некоторого момента продолжать рекламную кампанию невыгодно. При N*(t), близких к N₀*, уравнение (7*) записывается в виде

dN* (t) / d t = а₂N₀* (N₀* – N*).

Его решение стремится при t→∞ к предельному значению N₀* (а функция N(t) к N₀) по медленному экспоненциальному закону. В единицу времени появляется малое число покупателей. И поступающая прибыль не может покрыть продолжающихся издержек.

Аналогичный подход может быть использован при анализе внедрения технологических и других новшеств.

VIII. Двухвидовая борьба в популяции

Модели различных видов соперничества – двухвидовой борьбы в популяциях, гонки вооружений, боевых действий имеют общность методологических подходов, применяемых при получении и анализе этих моделей. По аналогии с осциллятором просматривается задача определения колебаний при взаимодействии двух биологических популяций.

Опишем эволюцию популяций, связанную с сосуществованием различных видов животных в ситуации "хищник – жертва". "Соперничество" жертвы с хищником выражается в изменении численности жертвы, которая в свою очередь сказывается на численности хищника.

Пусть М (t) – число "хищников" (больших рыб), которые питаются "жертвами" (малыми рыбами), число которых обозначим через N (t). Тогда число М (рыб-хищников) будет расти до тех пор, пока у них будет достаточно пищи, т.е. N (рыб-жертв), но в конце концов наступит такая ситуация, когда корма не будет хватать, и число "хищников" М начнет уменьшаться. Это приведет к тому, что число "жертв" (малых рыб) станет снова увеличиваться. Это будет способствовать новому росту числа "хищников" (больших рыб), и цикл повторится.

Математическую модель двухвидовой системы "хищник – жертва" рассмотрим при предположениях:

- численности популяций N (t) и М (t) зависят только от времени;

- в отсутствие взаимодействия численность видов изменяется по модели Мальтуса, при этом число жертв увеличивается, число хищников уменьшается (нечем питаться):

dN/dt = а N, dМ/dt = - β М;

- естественная смертность жертвы и естественная рождаемость хищника считаются несущественными;

- эффект насыщения численности обеих популяций не учитывается;

- скорость роста численности жертвы уменьшается пропорционально численности хищников, т.е. величине βМ, темп роста хищников, увеличивается пропорционально численности жертвы, т.е. величине аN.

Скорость изменения N (t) складывается из скорости прироста рождаемости и скорости убывания благодаря соседству с "хищниками". Тогда имеем

dN /dt = (а – β М) N, (8)

где а > 0, β > 0, член β МN описывает вынужденное убывание жертв (естественной смертностью популяции пренебрегаем).

Численность второй популяции ("хищников") растет тем быстрее, чем больше численность первой, а при ее отсутствии уменьшается со скоростью, пропорциональной численности М (t) (тем самым ее рождаемость не учитывается, как и эффект насыщения):

dМ/dt = (-β + а N) М, (8а)

где а > 0, β > 0.

Их этих уравнений по начальным численностям N (0) = N₀ и М (0) = М₀ определяется численность популяции в любой момент t > 0.

Нелинейную систему уравнений (8), (8а) удобно исследовать в плоскости переменных N, М, для чего первое уравнение поделим на второе:

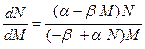. (8б)

Чтобы понять временную динамику функций N (t) и М (t), преобразуем уравнение (8б) к виду

dN (-β + а N) М = dМ (а – β М) N,

поделим обе части на величину N М и перенесем все члены в левую часть:

β dN/N - а₁ dN + а dM/M - β₁ dМ = 0

Интегрируя, получим

β lnN - а₁ N + а lnM - β₁ М = const,

где константа определяется по начальным значениям N (0) и М (0).

Или, уравнение (8б) имеет интеграл вида

lnN^β + lne^{-а1 N} + lnM^а + lne^{-β1 М} = C.

Потенцируя, получим интеграл в виде

N^β e^{-а1 N} = С₁M^-а e^{β1 М}, С₁ > 0.

Ответы на поставленные вопросы:

- если N (0) = N₀ и М (0) = М₀, то во все моменты времени численности популяций не изменяются;

- при малом (также как и при большом) отклонении от положения равновесия численности как хищника, так и жертвы не возвращаются к равновесным значениям – численности популяций совершают периодические колебания вокруг положения равновесия.

Очевидно, что система находится в равновесии (стационарное, не зависящее от времени решение) при М₀ = а β₁ и N ₀ = β/а₁ , когда dN/dt = dМ/dt = 0.

Рассмотрим устойчивость положения системы (8б) – как изменяются с течением времени начальные положения N ₀ и М₀, вернутся ли они в начальное положение при незначительном отклонении, какими будут их значения при существенном отклонении от начальных значений.

Рассмотрим малые отклонения системы от равновесных значений, т.е. представим решение в виде N = N ₀ + n, М = М ₀ + m. Подставляя N и М в (8), (8а), получим, отбрасывая члены более высокого порядка малости,

dn/dt = - β₁ N ₀m, (8с)

dm/dt = - а₁ М₀n. (8д)

Дифференцируя (8с) по t и подставляя в полученное уравнение функцию dm/dt, определяемую из (8с), придем к уравнению d² n /dt² = - а β n,

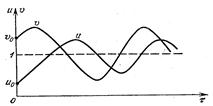аналогичному по форме базовому уравнению колебаний.

Следовательно, в системе происходят малые колебания численности с частотой 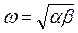, зависящей только от коэффициентов рождаемости и смертности а и β.

Величина m (t) подчиняется такому же уравнению, причем, если отклонение n (t) равно нулю в начальный момент t = 0, то m (t = 0) имеет максимальную амплитуду, и наоборот. Эта ситуация, когда численности n (t) и m (t) находятся в противофазе, воспроизводится для всех моментов t_i = iT/4, i = 1, 2, . . . , (T - период колебаний) и отражает запаздывание реакции численности одной популяции на изменение численности другой.

Любое решение системы (8), (8а) можно интерпретировать как кривую в трехмерном пространстве t, N, M – интегральную кривую. Проекция интегральной кривой на фазовое пространство N, M – фазовая траектория. Производные по времени можно интерпретировать как скорости изменения переменных N и М. Вектор скорости в каждой точке фазового пространства задается величиной правой части соответствующего уравнения в данной точке фазового пространства.

Рассмотрим N и M как координаты точки F (N, M) на плоскости, а изменения N и M как соответствующее движение этой точки F (N, M). При своем движении точка F (N, M) описывает некоторую кривую.

Любые колебания представляют собой движение с переменным ускорением, отклонение, скорость и ускорение в этом случае являются функциями времени. Для любых колебаний характерна периодичность, т.е. движение повторяется по истечении времени Т (период колебаний). Гармонические (синусоидальные) колебания можно представить в виде проекции равномерного движения по окружности.

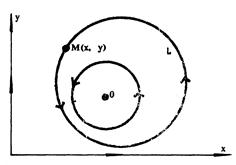На рисунке изображены фазовые траектории системы, стрелками показано направление траектории движения с течением времени.

В точке равновесия О численности N и M не меняются, кривой L соответствуют периодические колебания численностей N и M. Так как кривая L замкнутая, то точка F (N, M) вновь и вновь обегает эту кривую, что означает периодическое изменение численностей жертв N и хищников M.

Таким образом, численности жертв и хищников периодически колеблются, определенным образом согласованно.

Модель может быть уточнена учетом насыщения хищников. В этом случае фазовых траекторий уже несколько – в зависимости от соотношений параметров насыщения.

Ниже приведено три рисунка, каждый из которых соответствует некоторому типу соотношений хищник – жертва.

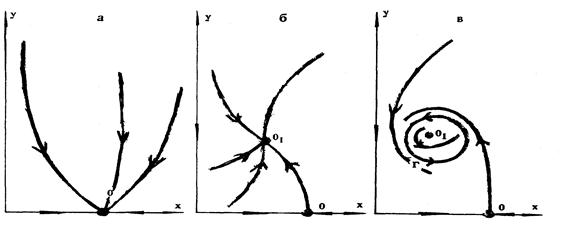
Случай а – хищники вымирают, жертвы достигают равновесного значения.

Случай б - хищники и жертвы сосуществуют, приходя к равновесным постоянным численностям в состоянии равновесия О₁.

Случай в – численности хищников и жертв все время меняются, приближаясь со временем к периодическим колебаниям.

IX. Взаимоотношения «производитель – управленец».

Несмотря на то, что взаимоотношения производителей и управленцев (чиновников) существенно отличаются от взаимоотношений «хищник – жертва», однако и те и другие находятся в конкурентных взаимоотношениях: производители питают управленцев, но и заинтересованы в них (управленцы способствуют производству продукта необходимого для обоих). Таким образом, имеются производители N, управленцы M, накопленный производенный продукт Р.

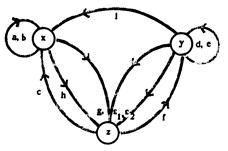Структурная схема, раскрывающая наличие и значимость связей между этими категориями, представлена на рисунке.

Каждая стрелка схемы соответствует наличию воздействия. Стрелка от Р к N, означает, что изменение N зависит от Р, стрелка от N к N - изменение N зависит от N. Все стрелки, идущие от N, M и Р, указывают, что изменение накопленного продукта Р зависит от N, M и Р.

Характер и вид этих влияний может быть описан математической моделью типа:

dN /dt = (а – β N - l M + c P) N,

dМ/dt = (-d - e M + fP) М, (9)

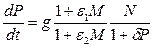- hN – kM = F

Коэффициент пропорциональности (а – β N - l M + c P) в первом уравнении убывает с N и M и растет с Р, что отражает внутреннюю конкуренцию среди производителей N, давление на них управленцев M и способствование производителям накопленного продукта Р. Параметр с отражает уровень использования накопленного продукта производителями.

Коэффициент пропорциональности (-d - e M + f P) М во втором уравнении убывает с M и растет с Р, что отражает внутреннюю конкуренцию управленцев M и благоприятствование росту управленцев накопленного продукта Р. Параметр d отражает жизнестойкость управленцев, параметр f - уровень использования накопленного продукта управленцами (способствование накопленного продукта существованию управленцев). Разница в знаках перед коэффициентами а и d соответствует возможности самостоятельного существования производителей и невозможности его для управленцев. Параметры е и l отражают уровень внутренней конкуренции управленцев.

Третье уравнение отражает производство, накопление и потребление продукта Р. Он производится совместными усилиями производителей и управленцев, потребляют его и те и другие. Параметры h и к отражают уровни потребления накопленного продукта производителями и управленцами, параметр d отражает умение общества сберегать накопленный продукт и наличие необходимых природных ресурсов.

Характер участия производителей и управленцев в производстве продукта разный: производители непосредственно его производят, управленцы способствуют производству. В соответствии с этим правая часть уравнения для Р содержит три слагаемых: первое соответствует скорости производства, второе и третье – потреблению производителями и управленцами.

Производство продукта пропорционально числу производителей N, коэффициент пропорциональности g соответствует технологическому уровню производства, коэффициент 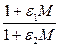- влиянию на производство управленцев, коэффициент 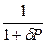, убывающий с ростом Р – амортизации накопленного продукта и трудности его накопления (когда продукта уже много).

Коэффициент влияния на производство управленцев 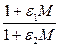меняется при изменении M от 1 до ε₁/ε₂, т.е. с ростом числа управленцев их влияние увеличивается, но ограничено некоторым пределом, в то время, как в отношении производителей такого предела нет.

Продукт понимается обобщенно – это не только потребительские товары, но и интеллектуальный продукт. Производители и управленцы также понимаются неоднозначно и обобщенно. Приведенная модель является достаточно упрощенной, очень многое ею не учитывается, но она дает возможность качественно описать взаимодействие производителей и управленцев. Анализируя модель, можно определить влияние каждого параметра на поведение модели.

Конкретизация и уточнение приведет к значительному усложнению модели, при этом количественная картина существенно не улучшится, но качественное описание существенно усложнится.

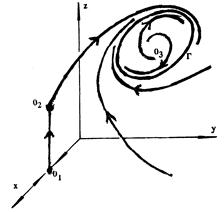
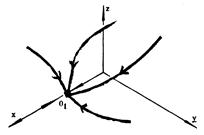Изменение в сообществе производителей и управленцев характеризуется изменением переменных N, M и Р, что графически может быть отражено в трехмерном пространстве, точки О – точки равновесия, изменения изображаются некоторыми кривыми, периодическое изменение – замкнутой кривой.

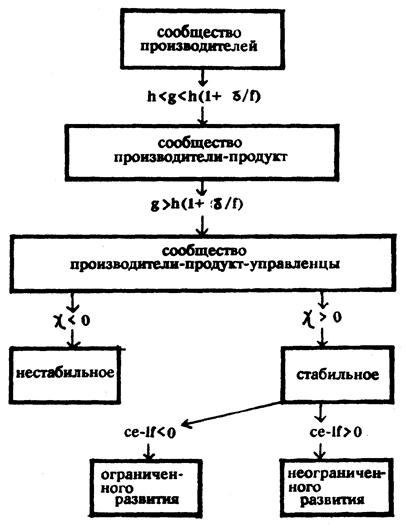
Характер сообщества сильно зависит от общего уровня его технологии, характеризуемого параметром g. При

g < h – низкий уровень технологии;

h < g < [1 + (dd/f)] – средний уровень технологии;

g > [1 + (dd/f)] - высокий уровень технологии.

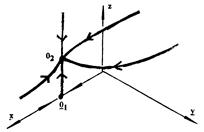Все кривые сходятся в точке О₁, т. е. к равновесию. Сообщество с низким уровнем технологии состоит из одних производителей – со временем переменные меняются так, что происходит переход любого сообщества к сообществу из одних производителей.

Координаты Р и M равны нулю - потребляется все, что производится, управленцы постепенно исчезают.

При увеличении уровня технологии до среднего значения характер изменения системы почти тот же, но у состояния равновесия О₂ нулю равна только одна координата - M (управленцы). В таком сообществе кроме производителей имеется уже накопленный продукт Р – сообщество может производить продукта больше, чем сразу потребляет, но управленцы в таком сообществе исчезают.

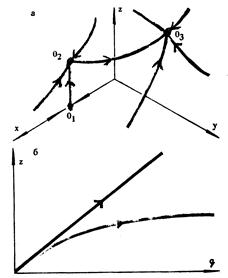
При дальнейшем увеличении уровня технологичности g сверх [1 + (dd/f)] при любых изменениях уровни равновесия сообщества достигаются тогда, когда в нем кроме производителей уже есть и накопленный продукт и в связи с этим могут появиться управленцы. Уровень технологии превышает величину [1 + (dd/f)], не зависящую от параметров ε₁ и ε₂, характеризующих способствование управленцев производству. Этот порог не зависит и от того, как интенсивно управленцы потребляют продукт (параметр к).

Поскольку параметры h и к отражают уровни потребления накопленного продукта производителями и управленцами, параметр f отражает способствование накопленного продукта существованию управленцев, то чем меньше h и больше f, тем раньше возникают управленцы. При этом играют роль также параметр d (отражает жизнестойкость управленцев) и параметр d (отражает умение общества сберегать накопленный продукт и наличие необходимых природных ресурсов).

Сообщество с высоким уровнем технологии может развиваться по разному, в зависимости от других параметров.

В стабильных сообществах переменные N, M и Р приходят к равновесным значениям, отвечающим равновесию О₃, в котором есть производители, накопленный продукт, управленцы. Равновесия О₁ и О₂, соответствующим сообществам без управленцев, неустойчивы.

Ниже на рисунке приведена зависимость накопленного продукта от уровня технологии (два варианта). Первый вариант – с ростом технологии неограниченно растет накопленный продукт Р (прямая). Второй вариант - с ростом технологии неограниченно накопленный продукт Р (также как и равновесные значения N и M) остается меньше некоторой величины – сообщество с ограниченным развитием (возможно, тупиковывй путь).

Развитие этих стабильных сообществ связано с величиной (ce – lf): при (ce – lf) > 0 общество развивается неограниченно, при (ce – lf) < 0 - ограниченно.

Параметр с отражает уровень использования накопленного продукта производителями, f - уровень использования накопленного продукта управленцами, е и l - уровень внутренней конкуренции управленцев. Величина (ce – lf) не включает ни параметров производства, ни параметров непосредственного потребления.

Для неограниченно развивающегося сообщества условие (ce – lf) > 0 можно записать в виде c/f > l/e, из чего следует, что возможность развития требует, чтобы отношения параметров и способствования накопленного продукта производителям и управленцам превышало отношение параметров давления управленцев на производителей к параметру внутреннего давления управленцев друг на друга.

Нестабильность сообщества вызывается потерей устойчивости равновесным состоянием (точка О₃) и возникающим вследствие этого колебательным процессом изменения переменных N, M и Р (кривая Г). При этом количество накопленного продукта Р то увеличивается, то уменьшается. Так же меняются и величины N и M.

Обозначим через g величину, от которой зависит стабильность сообщества. С обращением в нуль и переходом от положительным значениям к отрицательным происходит переход от стабильного общества к нестабильному (выражение g через параметры модели достаточно сложное и не приводится). Частный случай: при ε₁ = ε₂ и е = d = 0 имеет место нестабильность.

На рисунке качественно показано, в силу каких причин (значений параметров модели) сообщество имеет ту или иную организацию.

В модели не отражены роль науки, культуры, влияние различных отраслей промышленности, социальные отношения и т.д. и т.п.

7 МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ В ИССЛЕДОВАНИИ ОПЕРАЦИЙ

7.1 Моделирование операций распределения ресурсов

При выборе концепции системы возникают задачи оптимального распределении имеющихся ресурсов системы – задачи выбора решений (способа действий) при целенаправленном функционировании системы. Это может быть организация взаимодействия элементов, определение оптимальных режимов функционирования системы в различных условиях внешней среды.

Такие задачи возникают при организации производства и снабжения, эксплуатации транспортных систем, параметров конструкции, выбора средств производства, вооружения, в здравоохранении, бытовом обслуживании, связи, при боевых действиях и т.д.

Любое целенаправленное действие называется операцией. В общем случае – это совокупность взаимосвязанных действий всех компонентов системы, направленных на решение поставленной задачи.

Модель операции (операционная модель - формализованное описание факторов и связей между ними, отражающих ход операции) представляет собой совокупность, состоящую из субъекта, формирующего цель операции (оперирующей стороны), запаса активных средств (ресурсов) для проведения операции, набора стратегий, т.е. способов использования этих ресурсов, и критерия для сравнения различных стратегий достижения цели операции.

Модель операции разрабатывается на основе схемы операции, представленной в виде ряда последовательных этапов и элементарных действий компонентов для решения поставленной задачи (выполнения цели системы).

Степень соответствия результата операции поставленной ей цели (задаче) характеризуется критерием эффективности, который может зависеть от всех факторов, входящих в модель операции, в том числе, и неопределенных.

И управления, и неопределенные факторы могут быть функциями различной природы и сложности в зависимости от конкретных условий проведения операции, информированности оперирующей стороны.

Основная задача исследования операций – принятие решения о наилучшем способе достижения цели - выбор программы действий (способов использования ресурсов на выполнение операции) – решается методами математического программирования.

Основные разделы теории исследования операций: математическое программирование (линейное и нелинейное, детерминированное и стохастическое), теория принятия решений и теория игр, теория управления запасами, теория массового обслуживания, имитационное моделирование. Выбор метода решения диктуют тип и сложность исследуемой математической модели.

Общая модель операции выработки решения состоит из взаимосвязанных моделей: модели процесса операции (включая модель управляемой системы и модель обстановки проведения операции) и модели принятия решения. При этом учитываются физические и критериальные ограничения.

Физические ограничения ни при каких обстоятельствах не могут быть нарушены, поскольку они выражают законы сохранения.

Пример физических ограничений. Обозначим через q_i норму полива – количество воды, которое мы должны направить на орошение единицы земельной площади x_i. Тогда

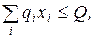
где Q - общее количество воды, которое накоплено в водохранилище.

Кроме того, суммарная площадь земли, которую можно использовать под посевы, также должна быть фиксирована, т.е. величины x_i должны удовлетворять еще одному ограничению:

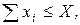
где Х – суммарная земельная площадь.

Критериальные ограничения определяются требованиями к конструкции и не являются такими жесткими – они находятся в распоряжении субъекта и в принципе могут быть нарушены или изменены.

Например, распределяя землю под посевы, необходимо добиться урожая максимальной стоимости, но при заданной структуре конечного продукта, или при проектировании самолета, кроме достижения его максимальной экономичности, могут быть ограничения на его крейсерскую скорость (не меньше заданной).

Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.

Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В этом и состоит специфика задач математического программирования: множество условий задается не системой уравнений, а системой неравенств, чаще всего экстремум достигается на границах множества условий, где нарушается принцип дифференцируемости, в практических задачах число переменных столь велико, что приводит к необходимости применения аналитических методов или эффективных вычислительных способов получения приближенного решения.

Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием.

Классификация задач математического программирования.

В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса: задачи линейного и нелинейного программирования.

Линейное программирование – целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств. В линейном программировании существуют классы задач, структура которых позволяет создать специальные эффективные методы их решения (например, транспортные задачи). Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.

Нелинейное программирование – нелинейны целевая функция и ограничения. Здесь выделяют: выпуклое программирование (выпукла целевая функция и множество, на котором решается экстремальная задача), квадратичное программирование (целевая функция квадратична, а ограничения – линейные равенства и неравенства).

В математическом программировании могут быть выделены два направления – решение детерминированных (вся исходная информация определена) и стохастических задач (параметры носят случайный характер с известными вероятностными характеристиками).

Формулировка задачи математического программирования

Задачи математического программирования, как правило, содержат большое число переменных и ограничений и не всегда допускают умозрительный анализ. Здесь требуется тщательная формализация и включение в математическую модель всех сколько-нибудь существенных ограничений.

Прежде чем построить математическую модель задачи, необходимо четко разобраться с ситуацией, описанной в условии. Для этого необходимо с точки зрения заданной задачи, а не математики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2) Какова цель решения? Какой параметр задачи служит критерием эффективности решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.

После предварительной постановки задачи получают ее формальное решение для простейших случаев, на которых можно проанализировать корректность поставленной задачи. На основании такого анализа вводятся дополнительные параметры и ограничения, проверяется корректность отнесения задачи к тому или иному классу, корректность введения линейности.

Общая схема формализации на основании содержательного описания задачи:

1.Определение переменных задачи (основных параметров).

2. Определение управляющих переменных, характеризующих существо действий и их элементарных составляющих.

3. Формулировка критериев эффективности через параметры и управляющие переменные.

4. Определение ограничений (области допустимых решений) через переменные задачи.

Задача математического программирования содержит n переменных x_i (i=1, 2,. . . , n), образующих n-мерный вектор переменных х.

На переменные накладываются ограничения - в форме равенств h_i(x) = 0, i = 1, . . . , p или неравенств g_i(x) ≥ 0, i = 1, . . . , q.

f(x) – целевая функция (в общем случае нелинейная) всех или некоторых переменных x_i (i=1, 2,. . . , n).

Задача математического программирования формулируется следующим образом:

Минимизировать (или максимизировать) f(x) при условиях g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p. Или кратко Min { f(x)│ g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p}.

7.2 Модели линейного программирования

Линейное программирование применяется при решении задач оптимального распределения ресурсов, управления и планирования производства; определения оптимального размещения оборудования; оптимального плана перевозок груза (транспортная задача) и т.д.

Задачи линейного программирования - оптимизационные. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.

Несмотря на различные области приложения, данные задачи имеют единую постановку:

найти значения переменных x₁, …, x_n, доставляющие оптимум заданной линейной формы z=c₁x₁ + c₂x₂+… + c_nx_n при выполнении системы ограничений, представляющих собой также линейные формы.

В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.

Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели свойств пропорциональности, аддитивности.

Основные допущения при построении линейных моделей:

- пропорциональность;

- аддитивность;

-. неотрицательность (не может быть отрицательного объема производства).

Пропорциональность - затраты ресурсов пропорциональны объему производства - вклад каждой переменной в целевой функционал и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной.

Например, если, продавая j-й товар в общем случае по фиксированной цене, фирма будет делать скидку при определенном уровне закупки до более низкого уровня цены, то будет отсутствовать прямая пропорциональность между доходом фирмы и количеством проданного товара. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что целевой функционал и ограничения должны представлять собой сумму вкладов от различных переменных. Величина, соответствующая целому объему всегда равна сумме величин, соответствующих его частям при любом способе разбиения на части.

Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Некоторые параметры задачи (финансы, запасы сырья, производственные мощности и др.) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения.

Формулировка общей задачи линейного программирования.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Каждая совокупность значений переменных (аргументов функции f), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция f, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции f, называется оптимальным планом задачи.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Нужно определить максимум или минимум линейной целевой функции (линейной формы)

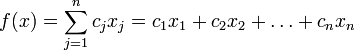
при ограничениях в виде равенств или неравенств

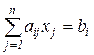, i = 1, . . . , r;

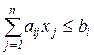, i = r+1, . . . , g;

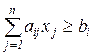, i = g+1, . . . , m;

x_ij ≥ 0 - требование неотрицательности управляющей переменной

где x_j, j=1, . . ., n – управляющие переменные, или решения задачи,

b_i, a_ij, i=1, . . ., m, j=1, . . ., n – параметры,

f – целевая функция.

Задача содержит n переменных и m ограничений.

Множество точек, удовлетворяющих системе ограничений, называется допустимым множеством (областью). Любая точка этого множества называется допустимой точкой (решением, планом). Линейная функция называется целевой функцией. Допустимая точка, которая минимизирует (максимизирует) функцию цели, называется оптимальным планом – решением задачи линейного программирования.

В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, ..., х_n являются неотрицательными.

Естественным решением сформулированной задачи линейного программирования является метод простого перебора: найти произвольное решение х₁ в допустимой области, вычислить (с, х₁), затем найти другое решение х₂, вычислить (с, х₂) и т.д. и среди полученных значений целевой функции (с, х) выбрать наименьшее. Этот путь перебора оказывается нереализуемым в связи со сложностью поиска допустимых решений, (допустимая область решений имеет бесконечное множество точек) и невозможностью поиска всех допустимых решений. Для решения задач линейного программирования строятся такие схемы поиска, которые позволяют выбирать оптимальный план, не перебирая всех возможных вариантов.

Типовые задачи линейного программирования

Методы линейного программирования позволяют описать широкий круг задач коммерческой деятельности, таких, как: планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров (транспортная задача); распределение работников торговли по должностям (задача о назначении); организация рациональных закупок продуктов питания (задача о диете); распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.

Дата добавления: 2014-08-04; просмотров: 691; Нарушение авторских прав

Мы поможем в написании ваших работ!