
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Транспортная задача
|
Читайте также: |
Транспортные модели описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи — определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. От того, насколько рационально будет прикрепление пунктов потребления к пунктам производства, зависит объем транспортной работы.
В качестве критерия оптимальности можно принять минимальную стоимость перевозок всего груза (общие транспортные расходы), либо минимальное время его доставки. Рассмотрим задачу с первым критерием.
Возникает задача о наиболее рациональном прикреплении потребителей к поставщикам, при котором удовлетворяются их потребности, а суммарные затраты на перевозку минимальны. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.
Параметры задачи.
Имеется m пунктов производства А1, …, Аm однородного продукта и n пунктов потребления В1,…, В n.
Предложение поставщика в каждом i-м пункте составляет аi единиц, i = 1, . . ., m.
Спрос потребителя в каждого j-ом пункте составляет bj единиц, j = 1, . . .. n.
Транспортные расходы на перевозку единицы продукции из Аi в Вj составляет cij (себестоимость, расстояние, тариф, время, расход топлива).
Требуется определить оптимальный план перевозок, при котором суммарные транспортные расходы минимальны продукции (управляющий параметр - количество продукции, перевозимой от каждого поставщика к каждому потребителю).
Обозначим xij – количество продукции, перевозимой от i-го поставщика j-му потребителю
i = 1, . . ., m, j = 1, . . .. n.
Математическая модель задачи
Суммарные затраты на транспортировку из всех пунктов производства во все пункты потребления:
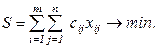 тр
тр
Управляющий параметр: xij ≥ 0 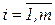 ,
, 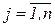 - количество единиц продукции, поставляемой из Аi в Вj – перевозки из пунктов потребления в пункты производства исключены.
- количество единиц продукции, поставляемой из Аi в Вj – перевозки из пунктов потребления в пункты производства исключены.
Ограничения
Суммарное предложение должно быть не меньше суммарного спроса
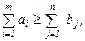
В каждый пункт потребления доставляется продукции не менее необходимой
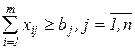 ,
,
От каждого поставщика вывозится продукции не более имеющейся
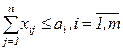 .
.
Всякое неотрицательное решение систем уравнений называется опорным планом (совокупность чисел xij , 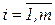 ,
, 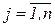 , удовлетворяющая приведенным ограничениям). Решение X*=(xij ), при котором функция S принимает минимальное значение - называется оптимальным планом транспортной задачи.
, удовлетворяющая приведенным ограничениям). Решение X*=(xij ), при котором функция S принимает минимальное значение - называется оптимальным планом транспортной задачи.
Это общая задача линейного программирования – ограничения в виде неравенств (несбалансированная транспортная модель).
Модель, в которой ограничения имеют вид равенств, называется сбалансированной транспортной моделью.
Несбалансированная модель может быть приведена к сбалансированной – неравенства заменены равенствами (в общем случае путем введения фиктивных неотрицательных переменных – фиктивного поставщика или потребителя продукции).
Замкнутая транспортная модель предполагает ограничения в виде равенств:
- сумма спроса равна сумме предложений;
- спрос каждого пункта потребления удовлетворяется полностью;
- весь продукт из каждого пункта производства должен быть вывезен.
Особая структура замкнутой транспортной задачи (все ограничения имеют вид равенств) позволяют решать ее простыми методами.
На пересечении i-ой строки и j-го столбца стоит тариф с и сюда же заносится значение хij – количество продукции, поставляемой от i-го поставщика j-му потребителю.
При большой размерности задачи (m x n) отыскание оптимального плана путем непосредственного перебора становится трудоемкой. Решение транспортной задачи состоит из двух этапов: нахождение начального плана, улучшение его и получение оптимального плана перевозок.
К рассмотренной транспортной задаче приводятся различные практические задачи, никак не связанные с планированием перевозок, но которые могут быть сформулированы в терминах транспортной задачи.
В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.
Хотя транспортная задача может быть решена как обычная задача линейного программирования, ее специальная структура позволяет разработать алгоритм с упрощенными вычислениями(на основе симплекс-метода).
Для решения транспортной задачи составляется транспортная таблица.
| Номер поставщика | Номер потребителя | Предло-жение | |||||
| . . . | j | . . . | n | ||||
| c11 x11 | c12 x12 | . . . | c1j x1j | . . . | c1n x1n | a1 | |
| c21 x21 | c22 x22 | . . . | c2j x2j | . . . | c2n x2n | a2 | |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| i | ci1 xi1 | ci2 xi2 | . . . | cij xij | . . . | cin xin | ai |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| m | cm1 xm1 | cm2 xm2 | . . . | cmj xmj | . . . | cmn xmn | am |
| Спрос | b1 | b2 | . . . | bj | . . . | bn |
Примеры сведения практических задач к канонической транспортной задаче
Многие практические задачи, связанные с планированием перевозок, не укладываются в рамки рассмотренной задачи, так как осложнены дополнительными ограничениями.
Суммарный объем производства больше потребления - может быть введен фиктивный пункт потребления Вn+1 с объемом потребления
bn+1 = 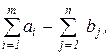 bn+1 – суммарный объем нереализованного продукта.
bn+1 – суммарный объем нереализованного продукта.
Размеры остатков в разных пунктах производства можно регулировать введением штрафа за единицу нереализованного продукта Аi.
Суммарный объем производства меньше потребления, то полное удовлетворение всех пунктов потребления невозможно. В этом случае необходимо организовать перевозки всего произведенного продукта так, чтобы наиболее важные пункты удовлетворялись полнее, и при этом суммарные транспортные расходы должны быть минимальны – вводится величина ущерба rj при неудовлетворении пункта Вj.
Требуется минимизировать суммарные затраты
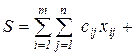
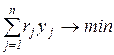
при условиях
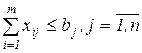 ,
, 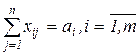 , xij > 0, yj = bj -
, xij > 0, yj = bj - 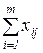 , где
, где
yj – разность между потребностями пункта Вj и поставками в него.
Перевозки с резервированием.
В некоторых районах пунктов производства может возникнуть необходимость в резервировании определенного количества продукта.
Iк – совокупность номеров i-го пункта производства в к-ом районе.
Требуется организовать перевозки таким образом, чтобы в к-ом районе (к=1,…,s) сохранилось не менее Vк единиц продукта.
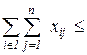
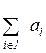 - Vк ,
- Vк , 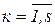 .
.
Общее число продуктов, вывезенных из всех пунктов производства к-го района должно быть не менее, чем на Vк (величину заданного резерва) меньше суммарного количества продукта, произведенного в этом районе.
Задача сводится к задаче транспортного типа 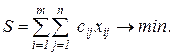
При условиях
 - удовлетворение спроса каждого пункта потребления;
- удовлетворение спроса каждого пункта потребления;
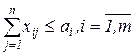 из каждого пункта производства не может быть вывезено продукта
из каждого пункта производства не может быть вывезено продукта
больше, чем производится;
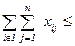
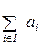 - Vк ,
- Vк , 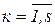 - условие резервирования;
- условие резервирования;
xij ≥ 0 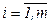 ,
, 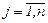 - объем перевозок неотрицательные числа (перевозки запрещены из пунктов потребления в пункты производства).
- объем перевозок неотрицательные числа (перевозки запрещены из пунктов потребления в пункты производства).
Пришли к задаче планирования перевозок, обеспечивающего удовлетворение спроса всех пунктов потребления, и гарантирующего сохранение требуемых резервов в каждом районе.
Ограничения на пропускные способности магистралей (в ограниченный промежуток времени) не позволят реализовать оптимальный план перевозок, полученный без учета этих ограничений.
В этом случае в транспортной задаче условие xij ≥ 0 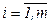 ,
, 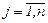 заменяется неравенством вида 0 ≤ xij ≤ dij, где dij – пропускная способность магистрали (ij), т.е. максимальный объем продукции, который может быть перевезен по этой магистрали за рассматриваемый промежуток времени. Такая задача может быть вообще неразрешимой (когда пропускная способность всех магистралей, ведущих к j-му потребителю меньше объема его потребностей).
заменяется неравенством вида 0 ≤ xij ≤ dij, где dij – пропускная способность магистрали (ij), т.е. максимальный объем продукции, который может быть перевезен по этой магистрали за рассматриваемый промежуток времени. Такая задача может быть вообще неразрешимой (когда пропускная способность всех магистралей, ведущих к j-му потребителю меньше объема его потребностей).
Перевозки с промежуточной обработкой.
Задача может быть осложнена наличием промежуточных транспортных узлов, в которых производится обработка груза (перевалка на другой вид транспорта, доработка полуфабриката перед поступлением его в пункт потребления).
А1,…, Аm – пункты производства с объемами производства а1, …, аm
В1,…, Вn – пункты потребления с объемами потребления b1,…, bn
С1,…, Ск – пункты промежуточной обработки.
Возможности пункта промежуточной обработки Сλ ограничены dλ единицами продукта.
Стоимости перевозки единицы полуфабриката продукта из Аi в Сλ составляет Сiλ‘, стоимость перевозки единицы полуфабриката продукта из Сλ в Вj составляет Сλj“.
Составить такой план перевозок, при котором весь полуфабрикат вывозится, полностью обрабатывается, потребности всех пунктов потребления удовлетворяются и при этом транспортные расходы минимальны.
Математическая модель.
Ziλj – количество продукта, доставляемое из пункта Аi в Вj через Сλ.
Транспортная таблица
| B1 | B2 | … | Bn | Bn+1 | Bn+2 | … | Bn+k-1 | Bn+k | ||
| А1 | M | M | M | c’11 | c’12 | c’1,k-1 | c’1k | a1 | ||
| А2 | M | M | M | c’21 | c’21 | c’2,k-1 | c’2k | a2 | ||
| ... | … | … | ||||||||
| Аm | M | M | M | c’m1 | c’m2 | c’m?k-1 | c’mk | am | ||
| Аm+1 | c”11 | c”12 | c”1n | M | M | M | d1 | |||
| Аm+2 | c”21 | c”21 | c”2n | M | M | M | d2 | |||
| … | … | |||||||||
| Аm+k-1 | c”k-1,1 | c”k-1,2 | c”k-1,n | M | M | … | M | dk-1 | ||
| Аm+k | c”k1 | c”k2 | c”kn | M | M | M | dk | |||
| b1 | B2 | … | Bn | d1 | d2 | … | dk-1 | dk |
Определить план перевозок {Ziλj}, на котором достигается минимум линейной формы
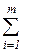
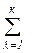
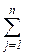 ( Сiλ‘ + Сλj“) Ziλj → min
( Сiλ‘ + Сλj“) Ziλj → min
при условиях
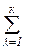
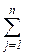 Ziλj = аi
Ziλj = аi 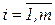
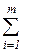
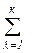 Ziλj = bj
Ziλj = bj 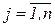
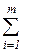
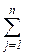 Ziλj ≤ dλ
Ziλj ≤ dλ 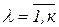
Ziλj ≥ 0, 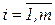 ,
, 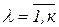 ,
, 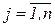
Необходимое и достаточное условие разрешимости задачи
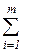 аi =
аi = 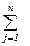 bj ≤
bj ≤ 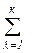 dλ
dλ
Преобразуем, введя новые переменные
xi,n+λ – количество полуфабриката, поступающее из пункта производства Аi в пункт обработки Сλ.
xm+λ,j - количество полуфабриката, поступающее из пункта обработки Сλ в пункт потребления Вj.
xi,n+λ = 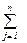 Ziλj ,
Ziλj , 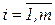 ,
, 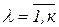 .
.
xm+λ,j = 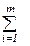 Ziλj,
Ziλj, 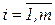 ,
, 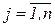 .
.
В новых переменных задача формулируется так: требуется минимизировать
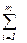
 Сiλ‘xi,n+λ +
Сiλ‘xi,n+λ + 
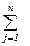 Сλj“ xm+λ,j
Сλj“ xm+λ,j
при условиях
 xi,n+λ = аi ,
xi,n+λ = аi , 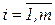 ,
,
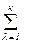 xm+λ,j = bj
xm+λ,j = bj 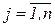 ,
,
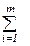 xi,n+λ =
xi,n+λ = 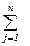 xm+λ,j ≤ dλ
xm+λ,j ≤ dλ 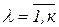
xi,n+λ ≥ 0, xm+λ,j ≥ 0, 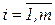 ,
, 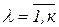 ,
, 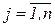 .
.
7.3 Распределительные задачи линейного программирования
Задачи распределения применяются при планировании множества операций, требующих одни и те же ресурсы и одно и то же оборудование. Предполагается, что каждая операция может быть выполнена многими способами, но для выполнения каждой операции наиболее подходящим путем не хватает ресурсов и оборудования. Задача заключается в том, чтобы, используя ограниченные мощности и наличные материалы, выполнить все работы оптимальным образом.
Задачи распределения в общем виде можно разделить на два вида:
1. Задан объем работ. Имеются определенные ресурсы, т.е. фиксированные производственные мощности и количество материалов. Необходимо найти такой вариант использования ресурсов, который обеспечит минимальные затраты на выполнение заданных работ;
2. Заданы определенные материалы и оборудование (ресурсы). Необходимо определить, какая работа дает максимальную прибыль при использовании этих ресурсов.
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие. Рассмотрим некоторые из них.
Примеры распределительных задач.
План снабжения предприятий. Имеются сырьевые базы и предприятия-потребители. Требуется разработать такой план снабжения сырьем каждого предприятия (с какой базы, в каком количестве, каким видом транспорта и какое сырье доставляется), чтобы потребности в сырье были обеспечены при минимальных расходах на перевозки. Здесь показатель эффективности – суммарные расходы на перевозки сырья в единицу времени (R → min).
Постройка участка магистрали. При постройке участка магистрали в распоряжении имеется определенные средства (трудовые и материальные ресурсы), требуется спланировать строительство (распределить ресурсы) так, чтобы строительство было завершено в минимальный срок. Здесь необходимо учитывать случайные факторы (метеоусловия, отказы техники), и тогда показатель эффективности – среднее ожидаемое время окончания строительства (Т → min).
Сеть торговых точек. Требуется спланировать количество торговых точек, их размещение, товарные запасы, чтобы обеспечить максимальную экономическую эффективность распродажи. Здесь показатель эффективности – средняя ожидаемая прибыль от реализации товаров (П → mах).
Задача о комплексном использовании сырья. Исходное сырье или материал может перерабатываться различными технологическими способами. В каждом случае получается в различном сочетании несколько видов продукции. Требуется найти план переработки, при котором заданные объемы конечной продукции получались бы с наименьшими затратами исходных материалов. Одним из распространенных примеров применения этого типа задач является оптимальный раскрой материалов.
Противолодочный рейд. Требуется рационально организовать боевую операцию по уничтожению подводной лодки группой самолетов (выбрать маршруты самолетов, высоту полета, способ атаки). Здесь показатель эффективности – вероятность того, что лодка будет уничтожена.
Распределение изделий между предприятиями (оборудования между участками) – минимизация суммарных затрат на изготовление всех изделий с учетом времени производства;
Регулирование парка вагонов (распределение вагонов разных типов под различные грузы) -минимизация суммарных затрат на погрузку;
Выбор рациональных пропорций производства и использования энергоресурсов при минимуме затрат (объем добычи угля и план распределения различных сортов угля между энергетическими установками, обеспечивающий их потребности наиболее экономным путем).
Рассмотрим некоторые примеры.
| <== предыдущая страница | | | следующая страница ==> |
| VII. Организация рекламной кампании | | | Распределение транспортных единиц по линиям |
Дата добавления: 2014-08-04; просмотров: 840; Нарушение авторских прав

Мы поможем в написании ваших работ!