Структура программ анализа по МКЭ на микроуровне

Основными частями программы анализа по МКЭ являются библиотеки конечных элементов, препроцессор, решатель и постпроцессор.

Библиотеки конечных элементов (КЭ) содержат модели КЭ – их матрицы жесткости. Очевидно, что модели КЭ будут различными для разных задач (анализ упругих или пластических деформаций, моделирование полей температур, электрических потенциалов и т.п.), разных форм КЭ (например, в двумерном случае – треугольные или четырехугольные элементы), разных наборов координатных функций.

Исходные данные для препроцессора - геометрическая модель объекта, чаще всего получаемая из подсистемы конструирования. Основная функция препроцессора – представление исследуемой среды (детали) в сеточном виде, т.е. в виде множества конечных элементов.

Решатель – программа, которая ассемблирует (собирает) модели отдельных КЭ в общую систему алгебраических уравнений и решает эту систему одним из методов разреженных матриц.

Построцессор служит для визуализации результатов решения в удобной для пользователя форме. В машиностроительных САПР это графическая форма. Пользователь может видеть исходную (до нагружения) и деформированную формы детали, поля напряжений, температур, потенциалов и т.п. в виде цветных изображений, в которых палитра цветов или интенсивность свечения характеризуют значения фазовой переменной.

Мировыми лидерами среди программ конечно–элементного анализа являются программно–методические комплексы Nastran, Ansys, Nisa, Adina, Cosmos. Как правило, эти комплексы включают в себя ряд программ, родственных по математическому обеспечению, интерфейсам, общности некоторых используемых модулей. Эти программы различаются ориентацией на разные приложения, степенью специализации, ценой или выполняемой обслуживающей функцией. Например, в комплексе Ansys основные решающие модули позволяют выполнять анализ механической прочности, теплопроводности, динамики жидкостей и газов, акустических и электромагнитных полей. Во все варианты программ входят пре– и постпроцессоры, а также интерфейс с базой данных. Предусмотрен экспорт (импорт) данных между Ansys и ведущими комплексами геометрического моделирования и машинной графики.

15.9. Математическое обеспечение анализа на функционально–логическом уровне

На функционально–логическом уровне исследуют устройства, в качестве элементов которых принимают достаточно сложные узлы и блоки, считавшиеся системами на макроуровне. Поэтому необходимо упростить представление моделей этих узлов и блоков по сравнению с их представлением на макроуровне. Другими словами, вместо полных моделей узлов и блоков нужно использовать их макромодели.

Вместо двух типов фазовых переменных в моделях функционально–логического уровня фигурируют переменные одного типа, называемые сигналами. Физический смысл сигнала, т.е. его отнесение к фазовым переменным типа потока или типа потенциала, конкретизируют в каждом случае исходя из особенностей задачи.

Основой моделирования аналоговых устройств на функционально–логическом уровне является использование аппарата передаточных функций. При этом модель каждого элемента представляют в виде уравнения вход–выход, т.е. в виде

Vвых = f(Vвх),

где Vвых и Vвх – сигналы на выходе и входе узла соответственно. Если узел имеет более чем один вход и один выход, то скаляры Vвых и Vвх становятся векторами.

Однако известно, что представление модели возможно только, если узел является безинерционным, т.е. в полной модели узла не фигурируют производные. Следовательно, для получения в общем случае требуется предварительная алгебраизация полной модели. Такую алгебраизацию выполняют с помощью интегральных преобразований, например,

с помощью преобразования Лапласа, переходя из временной области в пространство комплексной переменной р. Тогда в моделях типа имеют место не оригиналы, а изображения сигналов Vвых(р) и Vвх(р), сами же модели реальных блоков стараются по возможности максимально упростить и представить их моделями типовых блоков (звеньев) из числа заранее разработанных библиотечных моделей. Обычно модели звеньев имеют вид

Vвых(р) = h(p)Vвх(р),

где h(p) – передаточная функция звена.

В случае применения преобразования Лапласа появляются ограничения на использование нелинейных моделей, а именно: в моделях не должно быть нелинейных инерционных элементов. Другое упрощающее допущение при моделировании на функционально–логическом уровне – неучет влияния нагрузки на характеристики блоков. Действительно, подключение к выходу блока некоторого другого узла никак не влияет на модель блока.

Собственно получение математической модели системы (ММС) из математических моделей элементов (ММЭ) оказывается вследствие принятых допущений значительно проще, чем на макроуровне: ММС есть совокупность ММЭ, в которых отождествлены сигналы на соединенных входах и выходах элементов. Эта ММС представляет собой систему алгебраических уравнений.

Получение ММС проиллюстрируем простым примером (рис. 15.5), где показана система из трех блоков с передаточными функциями h1(p),

h2(p) и h3(p). ММС имеет вид:

V2 = h1(p)V1;

Vвых(p) = h2(p)V2;

V1 = Vвх(p) + h3(p)Vвых(p)

или

Vвых(p) =H(p)Vвх(p),

где H(p) = h1(p) h2(p) / (1 – h1(p) h2(p) h3(p)).

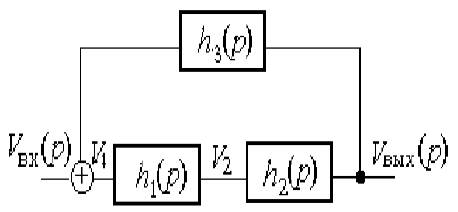
Рис.15.5. Пример схемы из трех блоков

Таким образом, анализ сводится к следующим операциям:

1) заданную схему устройства представляют совокупностью

звеньев и, если схема не полностью покрывается типовыми звеньями, то

разрабатывают оригинальные модели;

2) формируют ММС из моделей звеньев;

3) применяют прямое преобразование Лапласа к входным сигна-

лам;

4) решают систему уравнений ММС и находят изображения вы-

ходных сигналов;

5) с помощью обратного преобразования Лапласа возвращаются

во временную область из области комплексной переменной р.

Дата добавления: 2014-02-26; просмотров: 595; Нарушение авторских прав

Мы поможем в написании ваших работ!