
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ФИЗИЧЕСКИХ ПРОЦЕССОВ НА ОСНОВЕ АНАЛИЗА ИХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Цель этих операций – улучшение эстетических, органолептических и технологических свойств готовой продукции.
Вид отделочной операции зависит от вида полимерного материала, условий его эксплуатации.
К основным относятся:
- нанесение тонкой отделочной пленки на основной полимерных слой;
- нанесение рисунков тиснения и печать;
- придание замшевидности;
- удаление выпресовок, кромок и т.д.
Нанесение отделочной пленки
Эта операция называется поверхностной отделкой и ее используют в основном для отделки ИК и пленок, реже пластин.
В основном используют растворы полимеров в органических растворителях. Например для ПВХ – раствор ПВХ в смеси этилацетата и циклогексанона, для ПЭУ СК – растворы ПЭУ в ДМФА для ПА ИК- растворы ПА в спиртоводной смеси. Последнее время наметились тенденции к использованию для отделки составов без растворителей, например пластизолей ПВХ, водных дисперсий полимеров и др. Но это достаточно сложно, так как можно не достичь требуемой адгезии отделочного слоя к основному.
Наиболее типичный рецепт для отделки Винилискожи включает в себя следующие компоненты:
ПВХ-С
Полиметилметакрилат
Циклогексанон
Этилацетат
ДОФ
Наполнитель
Аэросил
Сочетание ПВХ и ПММА позволяет получать пленку бархатистую и мягкую на ощупь, т. е с очень хорошей органолептикой и хорошими оптическими свойствами. Кроме того, ПММА препятствует миграции пластификатора из лицевого покрытия на поверхность изделия.
Аэросил играет роль матирующего компонента и повышает устойчивость покрытия к действию УФ.
Для приготовления отделочных растворов применяют закрытые реакторы с различными мешалками (пропеллерными, якорными, и др.)
Нанесение отделочных покрытий осуществляют на наносных машинах, которые называются печатно-лакировальными агрегатами (рис. 1.65). Такие машины применяют, как для нанесения отделки, так и рисунка печать
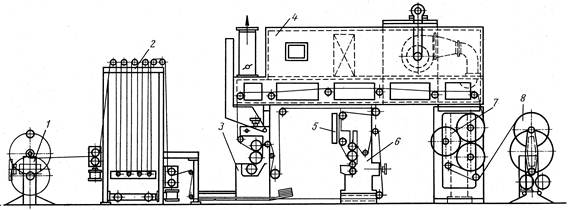
Рис. 1.65.
1- размоточное устройство, 2- компенсатор; 3-отделочный узел; 4- термокамера; 5- воздушно-сопловая сушилка; 6- печатный узел; 7- охлаждающие барабаны; 8-намоточное устройство.
Тиснение
Нанесение на гладкую поверхность рельефного рисунка.
Тиснение проводят на валковом оборудовании – тиснильных каландрах, пропуская материал между гладким прижимным валом с эластичным покрытием (обрезиненный) и металлическми валом с рельефным рисунком. Перед тиснением материал разогревают до вязкотекучего состояния, что позволяет легко наносить рисунок. Закрепляют рисунок последующим охлаждением. Тиснение может осуществляться сразу после желирования, желирования-вспенивания, каландрования.
При изготовлении мягких ИК переносным методом рисунок тиснение может быть нанесен на несущий транспортер подложку.
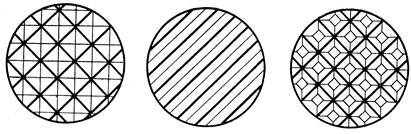
Рис. 1.66.
Образцы гравированных валов для тиснения.
Печать
Это операция нанесения печатного рисунка. В зависимости от конструкции печатного узла печать делят на высокую, офсетную и глубокую.
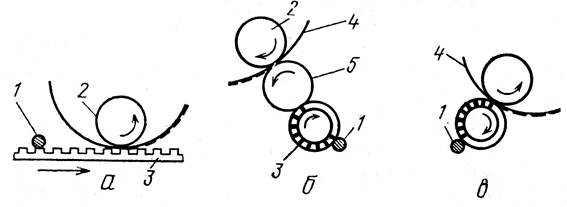
Рис. 1.67.
Высокая печать (а) по другому называется типографской. Краска наносится на выступающие элементы и переносится на запечатываемый материал. При этом способе печати - хорошая передача красок и четкий оттиск.
Офсетная печать (плоская) (б) Пробельные и печатные элементы находятся в одной плоскости Принцип основан на смачивании печатной формы увлажняющим раствором и накатывании жирной краски, которая при этом избирательно задерживается на несмачиваемых участках (печатных элементах) С печатной формы красочный оттиск переходит на резиновый офсетный вал, а с него на запечатываемый материал.
Глубокая печать – применение формного печатного вала, где печатающими элементами являются ячейки углубленные на поверхности формы, а пробельными промежутки между ними. Ячейки имеют различную глубину, изготовляют их методом фото травления. Печатный вал вращается в окрасочной ванне. Постоянно покрывается краской, которая тут же счищается с его поверхности специальным скребком. Самый распространенный и дешевый способ печати.
Концентрация раствора для печатной краски 5-20 %
Состав для ПВХ
ПВХ -С 7059 М
ПВДХ
ДОФ
Этилацетат
Бутилацетат
Циклогексанон
Стеариновая кислота
Пигмент
Приготовление печатного раствора см. ранее.
Существуют и другие способы печати, например, фотопечать, сублимационный и трафаретный. Все они применяются редко.
Нанести печать сложно, необходимо обеспечить адгезию, чтобы не было осыпания печатного рисунка. Хуже всего запечатываются полиолефины, например ПЭ. В этом случае перед нанесением печатной краски требуется специальная обработка поверхности ее травление за счет обработки коронным разрядом.
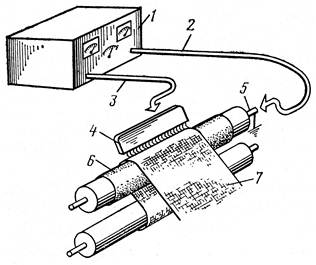
Рис. 1.68.
Установка для обработки ПЭ коронным разрядом
1- высоковольтная установка; 2- заземление; 3-высоковольтный провод; 4-5- электроды; 6- обрезиненный вал; 7 –полиэтиленовая пленка.
При действии установки образуется озон, под действием которого происходит окисление макромолекул в поверхностном слое ПЭ пленки, что делает его полярным, повышая адгезию к печатной краске.
В поседении годы широко применяют флексографическую печать(флексус-изогнутый). В этом способе используются эластичные или пластмассовые печатные формы и жидкие маловязкие быстросохнущие печатные краски. Сущность метода- передача печатной краски на запечатываемый материал через мягкие печатные формы, закрепленные на вращающемся формном цилиндре, к которому материал тыльной стороной прижимается печатным цилиндром. На печатные формы краска передается от жесткого накатного вала, на который она попадает от соприкосающего с ним вращающегося дукторного вала, захватывающего краску из ванны. Избыток печатной краски снимается ракельным ножом.
Флексографией можно наносить до 6-8 цветов. Скорость флексографии 400-600 м/мин.
Отделка под замшу
-шлифование (пример производство СК замши); (шлифовальные машины)
- метод блокирования - закрепление ворса в вертикальном положении в электростатическом поле;
-вымывание микрочастиц, нерастворимых для полимерной смеси;
- формирование покрытия обратным методом с использованием замшевидного транспортера-подложки.
Обрезка кромок, удаление выпресовок
Кромки обрезаются на дисковых ножах, установленных в поточных линиях по производству ИК и СК, а также на сортировочных столах.
Удаление выпресовок в производстве резин и литьевых изделий – дисковые ножи, установленные на тримминг-машинах.
Другие виды отделки
-Матирование (пропускание через матирующие валы)
-глянцевание –пропускание через зеркальные валы
- перфорация (например, пленка для экранов) - нанесение отверстий на проходных машинах.
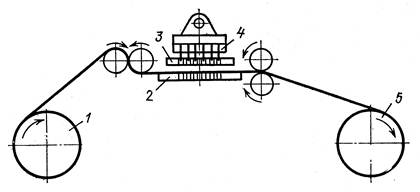
Рис. 1.69.
1-пленка;2-матрица; 3-направляющие колодки; 4-пуансон с резаками 5-перфорированная пленка.
-Мятие - обработка на мяльных станках, снабженных реверсивным барабаном на которых ИК хаотически заламывается и переваливается (придание мереи и кожеподобности);
- окрашивание подошв ( из пульвизаторов или окунанием) Лаки готовят на основе СЛ или раствором полимеров.
В производстве резин к отделочным можно отнести все операции идущие за вулканизацией: усадка, пролежка, двоение, Шпальтование
В производстве картонов - увлажнение, отволожка, каландрование, окрашивание и т д.
Металлизация– нанесение покрытий с использованием алюминия, хрома, меди, серебра (напыление металлов в вакууме (испарение нагретых металлов в вакууме и конденсация их паров на холодную поверхность полимера), дублирование полимерных материалов с фольгой, химическое осаждение из растворов солей.
Аппликация -накладные элементы из цветных материалов, которые закрепляют приклеиванием, сваркой, заформовыванием (закладка в форму при формовании)
Декалькомания –переводные картинки. Деколем и называют подложку с изображением. Изображение предварительно нанесено на подложку, с которой оно переводится на поверхность изделия.
Этот способ делят на мокрый, сухой и термический.
Мокрый требует предварительного намачивания деколя.
Второй сухой, подразумевает сныти е защитной пленки с деколя
Термический - деколь нагревается
Общими для любого вида продукции являются операции - Сортировка, маркировка, упаковка.
Вспомогательные процессы.
Абсорбция, адсорбция, Рекуперация. Ректификация стр. 115-124 и лекции по процессам и аппаратам .
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ФИЗИЧЕСКИХ ПРОЦЕССОВ НА ОСНОВЕ АНАЛИЗА ИХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Рассмотренные в предыдущих главах способы измерения основывались на использовании физической связи между величинами. При прямых измерениях, эти связи устанавливаются реально (физически) непосредственно в измерительных преобразователях. Например, в терморезисторе изменение температуры приводит к реальному изменению его сопротивления. В пружинных весах масса через механическое устройство преобразуется в реальный поворот указательной стрелки.
При косвенных измерениях эта связь задаётся физической формулой, связывающей измеряемую величину X сискомой величиной Y, где формула Y = f (X) есть выражение какого-либо физического определения или закона, записанного в виде алгебраического выражения.
В науке и технике могут возникать случаи, когда более целесообразным или даже единственно возможным оказывается другой способ, состоящий из двух этапов:
1)Строится математическая модель данного явления или процесса. Чаще всего, это обыкновенное дифференциальное уравнение, система обыкновенных дифференциальных уравнений, дифференциальное уравнение в частных производных или система таких уравнений;
2)Проводится математический анализ этой модели, в результате которого устанавливается связь между искомой величиной Y и другой величиной Ω, возникающей в процессе анализа
Y = f (Ω). (5.1)
Величина Ω либо может быть измерена непосредственно, либо определена путём косвенных измерений.
Этот способ может быть использован, если величина Y входит в начальное или граничное условие или характеризует источники и стоки, а также, характеризует какое – либо свойство среды. То есть является параметром рассматриваемого процесса, например постоянным значение температуры на одном из торцов нагреваемого стержня, или начальной концентрацией растворённого вещества в диффузионных задачах, или электропроводностью раствора при расчёте электростатического поля в растворе и так далее.
Ниже представлены две задачи из области технического контроля в водных растворах, поясняющие данный подход.
5.1. Определение параметра неравномерности тока на основе анализа электрического поля в датчике
В электрохимических производствах большое значение имеет контроль электрохимического параметра, который равен произведению удельной электропроводности раствора λ и удельного поляризационного сопротивления αна границе металл − электролит( 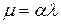 ). Поляризационное сопротивление имеет не омическую, а электрохимическую природу и характеризует торможение окислительных и восстановительных реакций в приграничном слое. Единица измерения величины λ равна [Ом−1·м−1], α − [Ом·м2], поэтому единицу измерения μ равна − [м]. Параметр μ определяет степень неравномерности плотности тока по поверхности металла, от которой зависит толщина и качество формируемого покрытия в гальваническом производстве или степень защиты металла от коррозии при его катодной поляризации.
). Поляризационное сопротивление имеет не омическую, а электрохимическую природу и характеризует торможение окислительных и восстановительных реакций в приграничном слое. Единица измерения величины λ равна [Ом−1·м−1], α − [Ом·м2], поэтому единицу измерения μ равна − [м]. Параметр μ определяет степень неравномерности плотности тока по поверхности металла, от которой зависит толщина и качество формируемого покрытия в гальваническом производстве или степень защиты металла от коррозии при его катодной поляризации.
Для установления зависимости (5.1) в рассматриваемом случае, сформулируем краевую задачу (дифференциальное уравнение и граничные условия), описывающую распределение электрического потенциала φ в полости трубы, заполненной электролитом [24].
Для простоты выводов будем считать радиус трубы R малым, порядка (5-10) мм, его длину не менее чем на порядок больше, электропроводность раствора достаточно высокой, выше 0.1 Ом-1·м-1 Это позволяет пренебречь изменением потенциала вдоль радиальной координаты r и свести задачу к решению обыкновенного дифференциального уравнения, решение которого  зависит только от продольной координаты. Выделим на трубе малый элемент длиной
зависит только от продольной координаты. Выделим на трубе малый элемент длиной 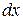 и запишем уравнение баланса втекающих и вытекающих токов (см. рис.5.1)
и запишем уравнение баланса втекающих и вытекающих токов (см. рис.5.1)

 , (5.2)
, (5.2)
где 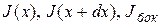 – соответственно ток, втекающий через сечение x, вытекающий через сечение
– соответственно ток, втекающий через сечение x, вытекающий через сечение  , вытекающий через боковую поверхность. Выразим токи через плотности токов
, вытекающий через боковую поверхность. Выразим токи через плотности токов 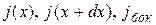
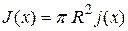 , (5.3)
, (5.3)
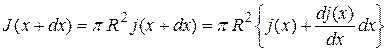 , (5.4)
, (5.4)
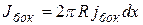 , (5.5)
, (5.5)
и подставив их в уравнение баланса, получим
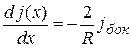 . (5.6)
. (5.6)
Связь между потенциалом и плотностью тока, протекающего через границу металл – электролит является линейной 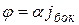 . Кроме того, учтём, что в толще раствора выполняется соотношение
. Кроме того, учтём, что в толще раствора выполняется соотношение 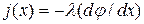 , представляющее собой закон Ома в дифференциальной форме. Тогда получим однородное обыкновенное дифференциальное уравнение второго порядка
, представляющее собой закон Ома в дифференциальной форме. Тогда получим однородное обыкновенное дифференциальное уравнение второго порядка
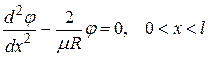 , (5.7)
, (5.7)
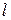 − длина трубы. Для удобства выводов поменяем направление оси на на противоположное. Пусть через левый торец трубы координатой
− длина трубы. Для удобства выводов поменяем направление оси на на противоположное. Пусть через левый торец трубы координатой 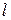 , в раствор подаётся ток J, который весь поглощается на поверхности и не выходит за пределы трубы (рис.5.2.а).
, в раствор подаётся ток J, который весь поглощается на поверхности и не выходит за пределы трубы (рис.5.2.а).
Тогда на концах выполняются граничные условия
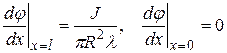 . (5.8)
. (5.8)
Дифференциальное уравнение (5.7) и граничные условия (5.8) образуют краевую задачу, которая является математической моделью явления распределения электростатического поля в растворе. Решение задачи (5.7), (5.8) не вызывает затруднений, с учётом второго граничного условия (5.8) оно имеет вид
 , (5.9)
, (5.9)
где А – константа интегрирования, ch(Z) – гиперболический косинус. Определив константу А из первого граничного условия (5.8), запишем
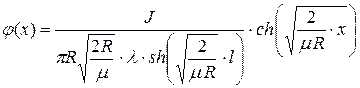 , (5.10)
, (5.10)
где sh(Z) – гиперболический синус. Путём непосредственной подстановки выражения (5.10) в дифференциальное уравнение и граничные условия, можно убедиться, что это выражение действительно является решением.
Учтём далее линейную связь между плотностью тока и потенциалом на границе металл-раствор, найдём распределение плотности тока в жидкости вдоль электрода
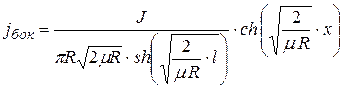 , (5.11)
, (5.11)
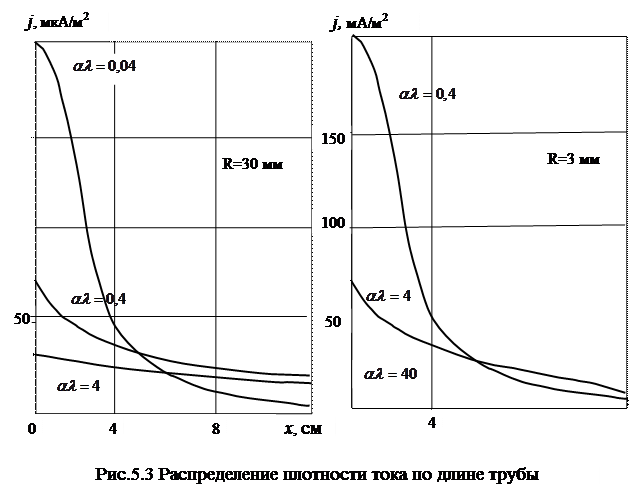
Полученное выражение (5.11) позволяет провести анализ неравномерности распределения плотности тока по поверхности трубы. В качестве примера приведём распределение при l=280 мм, R=30 мм и при l=280 мм, R=3 мм (рис.5.3),  выражено в метрах.
выражено в метрах.
Из графиков следует существование связи между степенью неравномерности плотности тока T и электрохимическим параметром 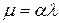
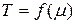 . (5.12)
. (5.12)
Многочисленные расчёты при других размерах электрода приводят к такому же выводу.
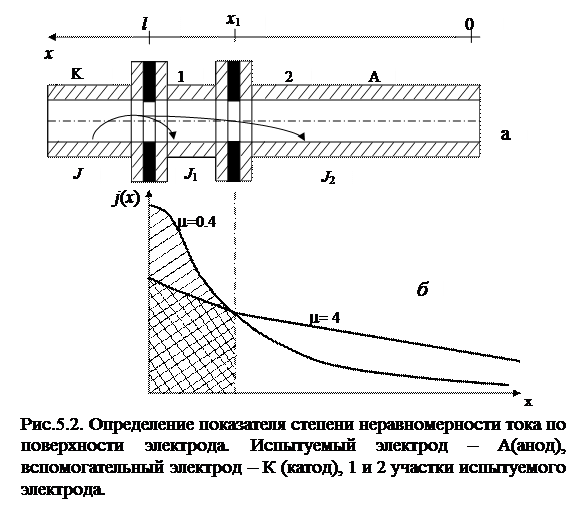
В качестве показателя неравномерности предложено использовать отношение тока J1 на одном из участков испытуемого электрода ко всему току на этом электроде J (T=J1/J), для чего электрод делят на два участка электрически разъединённые по металлу, но соединенные через устройство (на рисунке не показано) измеряющее ток J1(рис.5.2.б). Из этого рисунка видно, что чем выше степень неравномерности, тем больше значение тока 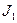 , который равен площади под кривой распределения плотности тока (заштрихованный участок). Учитывая сказанное, а так же постоянство J, отношение токов может быть выбрано в качестве показателя неравномерности
, который равен площади под кривой распределения плотности тока (заштрихованный участок). Учитывая сказанное, а так же постоянство J, отношение токов может быть выбрано в качестве показателя неравномерности
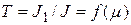 (5.13)
(5.13)
Участки 1 и 2 подключаются к одному и тому же полюсу источника питания и соединяются между собой через измерительное устройство с малым входным сопротивлением порядка 1 Ом. Поэтому они почти короткозамкнуты, и их, попрежнему, можно рассматривать как единый электрод. Поскольку стандартные микроамперметры имеют существенно большее входное сопротивление, в качестве устройства измеряющего ток 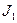 можно использовать резистор в один или менее Ом, к которому подключен микровольтметр.
можно использовать резистор в один или менее Ом, к которому подключен микровольтметр.
|
| |
| |


| |
| |


| |
| |
В данном методе не имеет значение, подключен ли испытуемый электрод как анод, или как катод, поскольку, учитывая линейность поляризационной зависимости при малой поляризации электродов, удельная поляризуемость 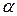 одинакова для обоих электродов
одинакова для обоих электродов
Получим выражение (5.13) математически, для этого определим ток J1 путём интегрирования выражение (5.11)
 , (5.14)
, (5.14)
где 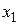 - координата разъединения участков 1 и 2. Показатель неравномерности имеет вид
- координата разъединения участков 1 и 2. Показатель неравномерности имеет вид
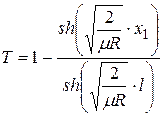 . (5.15)
. (5.15)
Таким образом, в качестве зависимости (5.1) в рассматриваемом случае выступает зависимости (5.15), в качестве искомой величины Y − электрохимический параметр μ, в качестве измеряемой величины Ω − электрический параметр неравномерности T. Подчеркнём, что зависимость(5.15) и параметр T появились в результате математического, а не физического анализа.
При заданных размерах электрода  , неравномерность распределения плотности тока определяется только электрохимическим параметром
, неравномерность распределения плотности тока определяется только электрохимическим параметром 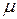 . Параметр
. Параметр 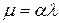 имеет большое значение при исследовании электрических полей в электролитах, делённый на характерный геометрический размер
имеет большое значение при исследовании электрических полей в электролитах, делённый на характерный геометрический размер 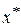 , он является электрохимическим безразмерным критерием подобия
, он является электрохимическим безразмерным критерием подобия  , указывает на соотношение между поляризационным
, указывает на соотношение между поляризационным 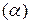 и омическим
и омическим 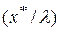 факторами при распределении тока в электролите и, следовательно, показывает степень неравномерности.
факторами при распределении тока в электролите и, следовательно, показывает степень неравномерности.
Задавая различные значения 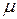 и рассчитав величину Т по формуле (5.15), получим численную или графическую зависимость (рис. 5.4). При заданных размерах электрода, эта зависимость рассчитывается один раз до начала эксплуатации датчика и используется во всех последующих измерениях на нём. Следовательно, она играет роль рабочей характеристики датчика. В случае промышленного производства, рабочая характеристика поставляется вместе с датчиком.
и рассчитав величину Т по формуле (5.15), получим численную или графическую зависимость (рис. 5.4). При заданных размерах электрода, эта зависимость рассчитывается один раз до начала эксплуатации датчика и используется во всех последующих измерениях на нём. Следовательно, она играет роль рабочей характеристики датчика. В случае промышленного производства, рабочая характеристика поставляется вместе с датчиком.
Сущность предложенного метода заключается в следующем. Подают на датчик ток 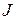 , измеряют ток
, измеряют ток  , рассчитывают показатель Т, используя рабочую характеристику, находят
, рассчитывают показатель Т, используя рабочую характеристику, находят 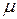 . Отметим, что таким способом можно получить именно произведение
. Отметим, что таким способом можно получить именно произведение 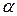 и
и 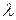 , а не каждую из этих величин по отдельности.
, а не каждую из этих величин по отдельности.
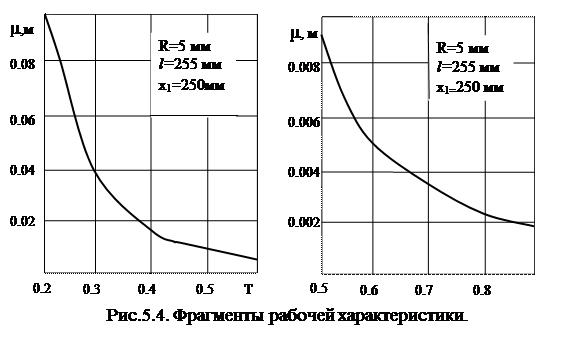
В качестве примера использования данного метода, рассмотрим контроль скорости коррозии нелегированной стали в неподвижной слабощелочном водном растворе с высоким солесодержанием при комнатной температуре. Измерения предложенным в данной работе методом осуществляли на электроде с размерами: x1= 30мм , l = 280мм , R = 30мм. Пересчет удельного поляризационного сопротивления в токовый показатель скорости коррозии (А/м2) проводился в соответствии с формулой Штерна-Гири [25] лежащей в основе как стандартного метода поляризационного сопротивления, так и предложенного метода
 (5.16)
(5.16)
Анодная и катодная константы Тафеля ba , bk для типичных коррозионных сред и конструкционных материалов представлены в справочной литературе [25], поэтому комбинацию этих констант можно рассматривать, как коэффициент пропорциональности.
При 20 0С по данным литературы ba = 0.059 мВ [25]. С учётом неподвижности воды и большой площади цилиндрического датчика, происходит значительный расход кислорода, который в данном случае может подводиться только диффузией. Наблюдается режим предельного диффузионного тока электрохимического восстановления кислорода. В этих условиях bk принимается равной бесконечности [25], тогда формула (5.16) принимает вид
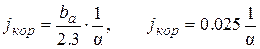 . (5.17)
. (5.17)
Результаты измерений и расчетов представлены в таблице 5.1. Электропроводность измерялась независимо стандартным лабораторным кондуктометром. Коэффициент пересчёта токового показателя в весовой показатель К (г/ м2·час)) равен для стали 1,04. Первое измерение проводилось через 4 часа после заливки раствора в датчик, и далее через сутки в течении четырёх суток. Средняя скорость коррозии по результатам экспресс – контроля оказалось равной (0.075±0.003) г/(м2·час). Скорость коррозии, измеренная в этих же условиях весовым методом равна (0.078-0.08) г/(м2·час).
Таблица 5.1
Результаты экспресc – контроля скорости коррозии
| τ, час | J1/J | µ, м | λ, Ом-1·м-1 | α, Ом·м2 | jкор, А/м2 | К, г/(м2·час) |
| 0.22 | 1.00 | 4.67 | 0.217 | 0.1178 | 0.122 | |
| 0.193 | 1.46 | 4.67 | 0.310 | 0.081 | 0.084 | |
| 0.177 | 1.87 | 4.67 | 0.400 | 0.063 | 0.065 | |
| 0.180 | 1.78 | 4.69 | 0.381 | 0.066 | 0.069 | |
| 0.173 | 2.02 | 4.69 | 0.428 | 0.059 | 0.061 |
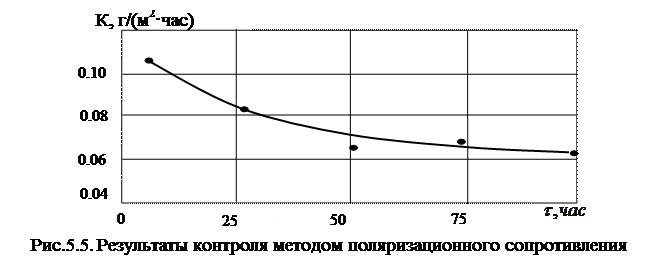 Рассмотренный эксперимент иллюстрирует преимущества предложенного метода, который позволяет определять не только среднюю, но и мгновенную скорость коррозии в любой момент времени.
Рассмотренный эксперимент иллюстрирует преимущества предложенного метода, который позволяет определять не только среднюю, но и мгновенную скорость коррозии в любой момент времени.
5.2.Контроль концентрации растворенного кислорода на основе анализа нестационарной диффузии его к катоду
Методы определения концентрации молекулярного кислорода, растворённого в водных растворах, применяются при контроле коррозионной агрессивности рабочих водных сред в теплоэнергетике и других областях техники, использующих тепломассообменное оборудование, а также при экологическом мониторинге окружающей водной среды.
Наибольшее распространение получил электродиффузионный (электрохимический) метод контроля, при котором через проточную электрохимическую ячейку, заполненную исследуемым раствором, пропускают постоянный электрический ток (см. рис.5.6). На катоде при этом происходит реакция электрохимического восстановления кислорода
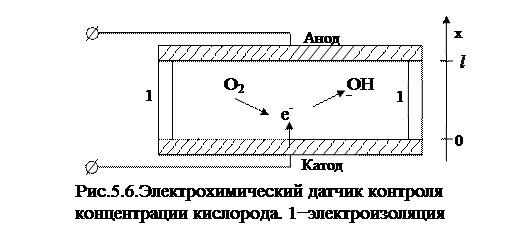
 , (5.18)
, (5.18)
с его поглощением. В глубине раствора подвод кислорода осуществляется вынужденной конвекцией, в прикатодном диффузионном слое – диффузией. На поверхности катода концентрация кислорода меньше, чем в глубине раствора, поэтому возникает градиент концентрации по нормали к катоду, и поток его равен 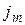
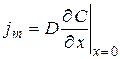 , (5.19)
, (5.19)
или приближенно
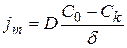 , (5.20)
, (5.20)
где 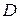 − коэффициент диффузии,
− коэффициент диффузии, 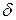 − толщина диффузионного слоя,
− толщина диффузионного слоя, 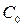 − концентрация кислорода в глубине жидкости,
− концентрация кислорода в глубине жидкости, 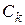 − концентрация его у поверхности катода. Контроль заключается в нахождении
− концентрация его у поверхности катода. Контроль заключается в нахождении 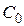 . Если устанавливается такой ток, для поддержания которого требуется весь кислород приэлектродного слоя, то
. Если устанавливается такой ток, для поддержания которого требуется весь кислород приэлектродного слоя, то  и
и
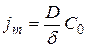 . (5.21)
. (5.21)
В этом случае возникает режим предельного диффузионного тока, электрический ток будет равен
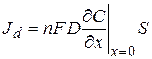 , (5.22)
, (5.22)
или приближенно
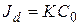 , где
, где 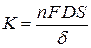 , (5.23)
, (5.23)
где  – число электронов участвующих в реакции,
– число электронов участвующих в реакции, 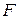 – константа Фарадея,
– константа Фарадея, 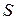 – площадь катода. Отградуировав амперметр на измерение концентрации
– площадь катода. Отградуировав амперметр на измерение концентрации 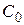 в соответствии с (5.23), можно измерять последнюю. Таким образом, рассмотренный случай − это пример прямого измерения.
в соответствии с (5.23), можно измерять последнюю. Таким образом, рассмотренный случай − это пример прямого измерения.
Всё сказанное относится к случаю стационарной диффузии, когда поток исследуемой жидкости стабилизирован, а толщина диффузионного слоя и предельный диффузионный ток постоянны во времени.
Основные затруднения в применении данного метода связаны с необходимостью обеспечить постоянство коэффициента пропорциональности 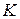 в формуле (5.23). При рассмотрении диффузионного слоя
в формуле (5.23). При рассмотрении диффузионного слоя 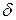 нужно отметить, что он является частью гидродинамического пограничного слоя
нужно отметить, что он является частью гидродинамического пограничного слоя 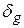 и зависит от кинематический коэффициент вязкости
и зависит от кинематический коэффициент вязкости 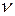 .Сам гидродинамический слой зависит от расстояния
.Сам гидродинамический слой зависит от расстояния 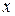 между рассматриваемой точкой электрода и точкой набегания потока жидкости, а также от скорости в ядре потока
между рассматриваемой точкой электрода и точкой набегания потока жидкости, а также от скорости в ядре потока 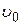
 ,
, 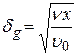 .
.
Следовательно, коэффициент пропорциональности 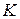 равен
равен
 .
.
Но величины входящие в этот коэффициент зависят от колебаний температуры, давления, состава раствора, степени шероховатости поверхности, скорости потока жидкости и т.д. Поэтому, коэффициент пропорциональности также может изменяться, а это приведет к неоднозначности в определении концентрации кислорода. Для обеспечения постоянства данного коэффициента, используют технически сложные кислородомеры с газопередающей системой, а рабочую поверхность катода покрывают специальной пленкой. При этом возникают свои технические проблемы.
Данных затруднений можно избежать, если рассматривать процесс нестационарной диффузии, когда жидкость внутри датчика неподвижна, а перенос кислорода осуществляется диффузией не только в диффузионном пограничном слое, но и во всем объеме. При этом, само понятие диффузионного слоя вряд ли применимо, скорее можно говорить о диффузионном фронте постепенно распространяющемся вглубь раствора. Поскольку процесс нестационарен, предельный диффузионный ток 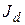 изменяется во времени.
изменяется во времени.
На основе решения краевой задачи нестационарной диффузии кислорода к катоду, работающему в режиме предельного диффузионного тока, предлагается рассчитать зависимость тока от времени, причём коэффициенты этой зависимости будут связаны с коэффициентом диффузии и начальной концентрацией кислорода 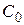 , подлежащей контролю в данном методе. Измеряя участок этой зависимости в эксперименте, и сопоставляя коэффициенты экспериментальной и расчетной зависимостей, определяют исходную концентрацию кислорода, а при необходимости и коэффициент его диффузии [25].
, подлежащей контролю в данном методе. Измеряя участок этой зависимости в эксперименте, и сопоставляя коэффициенты экспериментальной и расчетной зависимостей, определяют исходную концентрацию кислорода, а при необходимости и коэффициент его диффузии [25].
При таком подходе к проблеме, толщина диффузионного слоя 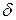 не участвует в определении искомой концентрации в виду отсутствия самого слоя. Коэффициент диффузии используется при контроле, но его не нужно знать заранее, так как он определяется в том же эксперименте, что и концентрация кислорода
не участвует в определении искомой концентрации в виду отсутствия самого слоя. Коэффициент диффузии используется при контроле, но его не нужно знать заранее, так как он определяется в том же эксперименте, что и концентрация кислорода 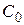 . В этом заключается преимущество предлагаемого метода.
. В этом заключается преимущество предлагаемого метода.
Для организации такого контроля нужно использовать непроточный герметичный датчик.
На начальном этапе толщина объема вовлеченного в процесс диффузии мала, диффузионный фронт медленно распространяется от катода к аноду. Для постановки математической задачи, важно знать: при каких условиях нужно считать анод расположенным на бесконечном расстоянии от катода? Ответ на этот вопрос зависит от того, на какое расстояние распространится диффузионный фронт за выбранный промежуток времени 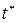 . Из соображений удобства проведения измерений, выберем промежуток времени между началом диффузии (подачей напряжения на электроды) и началом измерений
. Из соображений удобства проведения измерений, выберем промежуток времени между началом диффузии (подачей напряжения на электроды) и началом измерений 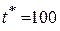 секунд. Если за это время процесс диффузии распространится на расстояние много меньшее, чем расстояние до анода, то анод следует считать расположенным на бесконечности. Так как коэффициент диффузии имеет размерность [мм2/с], его можно представить в виде
секунд. Если за это время процесс диффузии распространится на расстояние много меньшее, чем расстояние до анода, то анод следует считать расположенным на бесконечности. Так как коэффициент диффузии имеет размерность [мм2/с], его можно представить в виде
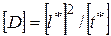 ,
,
где 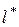 - характерный размер. При 250С коэффициент диффузии кислорода в воде равен
- характерный размер. При 250С коэффициент диффузии кислорода в воде равен 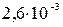 мм2/с, тогда
мм2/с, тогда 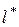 = 0,5 мм. Если расстояние до анода существенно больше, то следует считать, что координата
= 0,5 мм. Если расстояние до анода существенно больше, то следует считать, что координата 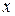 , направленная по нормали от катода в глубину раствора изменяется в интервале
, направленная по нормали от катода в глубину раствора изменяется в интервале 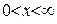 .
.
Обычно в кислородомерах напряжение на электроды подается потенциостатическим способом так, чтобы напряжение не изменялось, как бы не изменялось внутреннее электрическое сопротивление электрохимической ячейки. Кроме того, величина подаваемого напряжения должна сразу же после включения обеспечить режим предельного диффузионного тока. Тогда весь подводимый кислород без остатка расходуется в реакции (5.18). Поэтому его концентрация на катоде, где 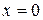 , равна нулю в любой момент времени
, равна нулю в любой момент времени
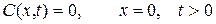 . (5.24)
. (5.24)
При математической постановке задачи соотношение (5.24) играет роль граничного условия. Кроме того, выполняется начальное условие
 , (5.25)
, (5.25)
которое означает, что в момент включения и до него кислород равномерно распределен по объему с исходной концентрацией 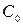 .
.
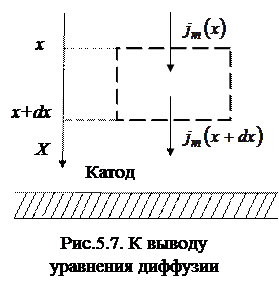 Выведем дифференциальное уравнение для процесса нестационарной диффузии кислорода в полости датчика, изображённого на рис.5.6, при условии, что расстояние между электродами порядка 1 мм. Выделим в растворе малый объёме (см.рис.5.7). Через верхнюю грань (x) втекает масса кислорода m(x), а через нижнюю − вытекает масса m(x+dx). Введём понятие плотности потока вещества jm(x), как массу проходящую через единицу поверхности dS в единицу времени dt. Используя, кроме того, первый закон Фика, который гласит, что плотность потока пропорциональна градиенту концентрации растворённого кислорода, запишем
Выведем дифференциальное уравнение для процесса нестационарной диффузии кислорода в полости датчика, изображённого на рис.5.6, при условии, что расстояние между электродами порядка 1 мм. Выделим в растворе малый объёме (см.рис.5.7). Через верхнюю грань (x) втекает масса кислорода m(x), а через нижнюю − вытекает масса m(x+dx). Введём понятие плотности потока вещества jm(x), как массу проходящую через единицу поверхности dS в единицу времени dt. Используя, кроме того, первый закон Фика, который гласит, что плотность потока пропорциональна градиенту концентрации растворённого кислорода, запишем
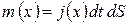 ,
, 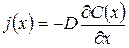
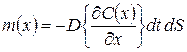 (5.26)
(5.26)
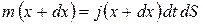 ,
, 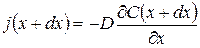 ,
,
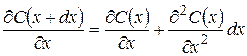 ,
,
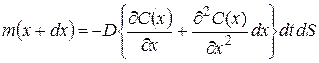 . (5.27)
. (5.27)
Поскольку задача нестационарная, то в выделенном объёме происходит изменение массы (а значит и концентрации кислорода) во времени
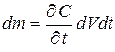 . (5.28)
. (5.28)
В выделенном объёме отсутствуют источники или стоки кислорода, поэтому изменение во времени возможно только за счёт разности втекающего и вытекающего потоков Δm
 . (5.29)
. (5.29)
Приравняв (5.28) и (5.29) и сократив на dVdt (dV = dxdS), получим дифференциальное уравнение нестационарной диффузии
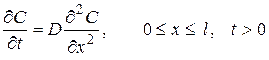 . (5.30)
. (5.30)
Плотность потока на границе анода и жидкости равна нулю, так как там не выделяет и не поглощает кислород. Тогда в соответствии с законном Фика, выполняется граничное условие
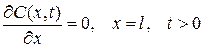 , (5.31)
, (5.31)
Дифференциальное уравнение (5.30), начальное условие (5.25) и граничные условия (5.24) и (5.31), образуют краевую задачу, которая является математической моделью процесса диффузии.
Решением данной краевой задачи является ряд
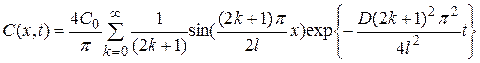 . (5.32)
. (5.32)
Непосредственной подстановкой можно убедиться, что этот ряд удовлетворяет и дифференциальному уравнению и условиям однозначности.
Вычислим производную на катоде
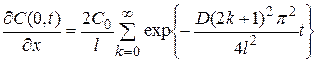 , (5.33)
, (5.33)
и оценим скорость сходимости этого ряда при 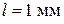 ,
, 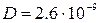 м2/с. В таблице 5.2 представлены первый (S1) и второй (S2) члены ряда (5.33)
м2/с. В таблице 5.2 представлены первый (S1) и второй (S2) члены ряда (5.33)
Таблица 5.2
Оценка сходимости ряда (5.33)
| t, c | S1 | S2 | S2/S1 |
| 0.895 | 0.368 | 0.41 | |
| 0.691 | 0.036 | 0.052 | |
| 0.574 | 0.0117 | 0.012 | |
| 0.477 | 0.0013 | 0.0027 |
в зависимости от времени. Из таблицы следует, что через 300 секунд после включения установки вторым и последующими членами этого ряда можно пренебречь, поскольку второй член ряда составляет 1 % от первого, остальные члены ряда пренебрежительно малые величины. Таким образом, можно ограничится только первым членом ряда.
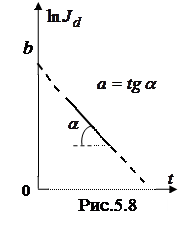 Используем формулу (5.22), рассчитаем зависимость предельного диффузионного тока от времени (учтено, что n=4)
Используем формулу (5.22), рассчитаем зависимость предельного диффузионного тока от времени (учтено, что n=4)
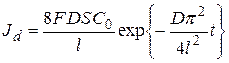 . (5.34)
. (5.34)
В полулогарифмических координатах она имеет вид прямой (рис. 5.8)
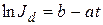 , (5.35)
, (5.35)
где константы 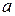 и
и 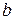 определяются по формулам:
определяются по формулам:
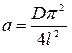 ,
, 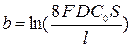 (5.36)
(5.36)
Измерив участок данной зависимости, находим в эксперименте 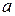 и
и 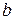 . Для этого строится регрессионная зависимость по методу наименьших квадратов (см. параграф 4.10), в соответствии с которой коэффициенты
. Для этого строится регрессионная зависимость по методу наименьших квадратов (см. параграф 4.10), в соответствии с которой коэффициенты 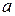 и
и 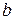 вычисляются по формулам
вычисляются по формулам
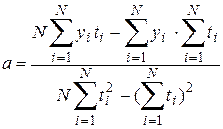 ,
, 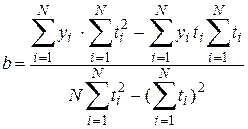 ,
,
где N − число измерений, 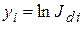 .
.
Определив 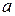 и
и 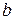 и подставляя их в формулы (5.36), находим концентрацию кислорода C0 и коэффициент диффузии D.
и подставляя их в формулы (5.36), находим концентрацию кислорода C0 и коэффициент диффузии D.
В качестве зависимости (5.1) в рассмотренном примере выступают соотношения (5.36), в качестве искомой величины Y − концентрация растворённого кислорода C0 и коэффициент его диффузии D, в качестве измеряемой величины Ω − коэффициенты 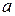 и
и 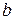 . Подчеркнём, что зависимости (5.36) и параметры a и b получены в результате математического, а не физического анализа.
. Подчеркнём, что зависимости (5.36) и параметры a и b получены в результате математического, а не физического анализа.
| <== предыдущая страница | | | следующая страница ==> |
| Отделочные операции | | | Охрана измененных человеком ландшафтов. Особо охраняемые природные территории. Заповедники |
Дата добавления: 2014-07-11; просмотров: 673; Нарушение авторских прав

Мы поможем в написании ваших работ!