Принцип максимума модуля целой функции f(z)

Принцип максимума модуля функции - утверждение, согласно которому аналитическая функция одного или нескольких комплексных переменных, отличная от постоянной, не может внутри области аналитичности достигать своего максимального по абсолютной величине значения. В частности, если f(z) – аналитическая функция в области D, и в некоторой окрестности U точки имеет место неравенство |f(z)| 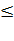|f( 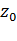)|, то f(z) постоянна в D.

Если f(z) аналитична в D и непрерывна в замыкании D, то функция |f(z)| достигает своего макс, значения на границе области D.

Дата добавления: 2014-07-14; просмотров: 351; Нарушение авторских прав

Мы поможем в написании ваших работ!