
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция №8. Парный линейный и нелинейный корреляционный анализ
Первое упоминание о металле, который по описанию был похож на алюминий, вст-речается в первом веке нашей эры у Плиния Старшего. Согласно изложенной им легенде, некий мастер преподнес императору Тиберию необычайно легкий и красивый кубок из серебристого металла. Даритель сообщил, что получил новый металл из обычной глины. Очевидно, он ожидал благодарности и покровительства, но вместо этого лишился жизни. Недальновидный правитель приказал обезглавить мастера и разрушить его мастерскую, чтобы предотвратить обесценивание золота и серебра.
На настоящий момент известны два пути получения алюминия – химический и электролитический. Первый шаг к получению алюминия сделал прославленный Пара-цельс в 16 веке. Он выделил из квасцов «квасцовую землю», содержавшую окись неведо-мого тогда металла. А в середине 18 века эксперимент повторил немецкий химик Андреас Маргграф (Andreas Marggraf). Он назвал окись алюминия словом «alumina» (от латинского «alumen» — вяжущий). С этого момента о существовании алюминия стало известно науке, однако, не будучи найденным в чистом виде, металл не получил настоящего признания.
В 1808 году англичанин Хэмфри Дэви (Humphry Davy) пытался выделить алюми-ний методом электролиза, но неудачно. Успехом увенчались эксперименты датчанина Ханса-Кристиана Эрстеда (Hans Christian Ørsted) в 1825 году. Пропустив хлор через рас-
каленную смесь глинозема с углем, он получил хлористый алюминий. Нагрев его с амаль- гамой калия, Эрстед выделил металл, по своим свойствам похожий на олово. Ученый со-общил об этом в малоизвестном журнале и прекратил эксперименты. Эстафету принял немец Фридрих Велер (Friedrich Wöhler). Он в 1827 году смог выделить крупинки алюми-ния, которые, однако, на воздухе немедленно покрывались тончайшей пленкой оксида алюминия. В итоге Велер потратил 18 лет работы на то, чтобы получить алюминий в виде слитка.
В 1854 году французский химик и промышленник Сент-Клер Девиль (Henri Saint-Claire Deville) разработал более дешевый способ. Он использовал в качестве восстано-вителя натрий, заменив им дорогостоящий калий. На Всемирной выставке 1855 года в Париже «серебро из глины» произвело фурор. Император Наполеон III, за столом кото-рого особо почетным гостям подавали приборы из алюминия, загорелся мечтой снабдить свою армию кирасами из легкого металла. Он оказал Девилю мощную поддержку, и тот построил несколько алюминиевых заводов. Но произведенный им металл по-прежнему оставался дорогим. Из него делали лишь ювелирные украшения и предметы роскоши. Начиная с 1855 года, когда был получен первый слиток алюминия, и по 1890 год, спосо-бом Сент-Клер Девиля было получено 200 тонн металлического алюминия. В 1856 году он же получил алюминий электролизом расплава хлорида натрия-алюминия.
В 1885 году был построен завод по производству алюминия в немецком городе Гмелингеме, работающий по технологии, предложенной Николаем Бекетовым. Техноло-гия Бекетова мало чем отличалась от способа Девиля, но была проще и заключалась во взаимодействии между криолитом (Na3AlF6) и магнием. За пять лет на этом заводе было получено около 58 т алюминия — более четверти всего мирового производства металла химическим путем в период с 1854 по 1890 год.
Более дешевый способ производства алюминия (электролитический) появился лишь к концу 19-го века. Его одновременно и независимо друг от друга разработали американский студент Чарльз Холл (Charles Hall) и французский инженер Поль Эру (Paul Héroult). Предложенный ими электролиз расплавленной в криолите окиси алюминия давал прекрасные результаты, но требовал большого количества электроэнергии. При строите- льстве первого завода эту проблему решили, разместив предприятие рядом со знаменитым Рейнским водопадом в Швейцарии. Работавший в России австрийский инженер Байер (Carl Josef Bayer) создал технологию получения глинозема, которая сделала новый способ еще более дешевым. Процессы Байера и Холла-Эру до сих пор применяются на современ-ных алюминиевых заводах.
Новый промышленный материал был хорош всем, за исключением одного: для не-которых сфер применения чистый алюминий был недостаточно прочен. Эту проблему решил немецкий химик Альфред Вильм (Alfred Wilm), сплавлявший его с незначитель-ными количествами меди, магния и марганца. Он открыл, что сплав в течение нескольких дней после закалки становится все прочнее и прочнее. В 1911 году в немецком Дюрене была выпущена партия названного в честь города дюралюминия, а в 1919 году из него был сделан первый самолет.
Вторая мировая война значительно стимулировала производство алюминия. Так, в 1939 году общемировое его производство, без учёта СССР, составляло 620 тыс. т, но уже к 1943 году выросло до 1,9 млн т., а к началу 21 века объем его производства достиг 24 мил-лионов тонн. Так началось триумфальное шествие алюминия по миру. Мировые запасы бокситов практически безграничны, то есть несоизмеримы с динамикой спроса. Сущест-вующие мощности могут производить до 44,3 млн. т первичного алюминия в год.
Контрольные вопросы для самопроверки.
1.Как распространен алюминий в земной коре?
2.Укажите основные свойства алюминия, необходимые в случае изготовления из него именно Вами художественного изделия.
3.Из каких основных полезных ископаемых извлекается алюминий?
4.Какие два пути существуют для получения алюминия из полезных ископаемых?
5.Какой способ получения алюминия применяется в настоящее время в промышленных масштабах?
6.Почему в 19 веке нельзя было широко использовать способ получения алюминия электролизом?
7. Почему в промышленности используются сплавы алюминия, а не чистый алюминий?
8.Чем обусловлено использование алюминия при изготовлении проводов?
9.Какой основной эффект мы получаем при использовании алюминия при изготовлении различного рода транспортных машин?
10.В чем недостатки использования алюминия при изготовлении столовых приборов?
11.Как использовали в 19 веке алюминий в ювелирной промышленности и почему мода на него в 20 веке прошла?
12.Какие алюминиевые сплавы используются для изготовления скульптурных композиций?
13.В чем состоят преимущества использования алюминия и его сплавов для экстерьерных работ?
14.Приведите примеры использования алюминия и его сплавов для интерьерных изделий.
15.К каким, с Вашей точки зрения, художественным направлениям лучше всего отвечает использование алюминия и его сплавов? Какие бы изделия Вы попробовали бы из него изготовить?
Лекция №8. Парный линейный и нелинейный корреляционный анализ
Для описания связей между варьирующими признаками (переменными) применяют математическое понятие функции f, которая ставит в соответствие каждому определенному значению независимой переменной Х, называемой аргументом, вполне определенное значение зависимой переменной Y: y=f(x). Такого рода однозначные зависимости Y от Х называются функциональными зависимостями или связями.
Однако чаще встречаются корреляционные связи или просто корреляции, когда определенному значению независимой переменной Х соответствует не одно и то же числовое значение Y, а распределяющийся вариационный ряд числовых значений зависимой переменной, хотя связь и записывается в том же виде, что и функциональная y=f(x).
Задачи корреляционного анализа сводятся к установлению направления (положительная или отрицательная), формы связи (линейная, точнее прямолинейная) или нелинейная (криволинейная), измерению ее тесноты (величины) и оценке значимости связи.
Графическое различие функциональной и корреляционной связи (рис. 1).
·
· · ·
· · · · ·
· · · · ·
· · · · ·
· · · · ·
· · ·
а б
Рис. 1. Функциональная (а) и корреляционная (б) положительная линейная связи
Не все корреляционные связи можно называть корреляционными зависимостями. Например, если измерить на каком-то участке леса высоту и диаметр дубов, между этими переменными будет обнаружена корреляционная связь. Но диаметр не зависит от высоты, как и высота от диаметра. Эти признаки корреляционно связаны потому, что они оба увеличиваются при росте деревьев. Связь есть – зависимости нет.
Корреляционные связи не обязательно свидетельствуют о причинно-следственных связях, но об этом подробнее поговорим позднее.
Коэффициент корреляции r
Показателем парной линейной связи является двумерная статистика коэффициент корреляции r.
rxy= 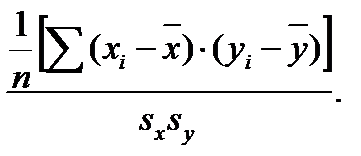
Коэффициент корреляции – отвлеченное число, лежащее в пределах от -1 до +1. При независимом варьировании признаков, когда связь между ними полностью отсутствует, r=0; при функциональной связи r=1 или r=-1 .
Знак перед r указывает на направление корреляции. Например, мы получили r=-0.9. Это значит, что связь отрицательная, сильная (тесная).
Проще всего оценивать значимость коэффициента корреляции, пользуясь уже составленными таблицами критических значений коэффициента корреляции rxy. Такая таблица имеется и у Лакина (1990) (табл. 1), правда табулированная лишь для 2-х уровней значимости (р=0.05 и р=0.01). Допустим, для нахождения r использовали 7 пар значений признака. В этом случае (см. табл. 1) значимым считается r>=0.75 (р=0.05) и r>=0.87 (р=0.01). При вычислении на ПК обычно получают оценки не только значений r, но и его значимости.
Таблица 1
Критические значения коэффициента корреляции rxy
| Степени свободы k=n-2 | Уровни значимости α, % | Степени свободы k=n-2 | Уровни значимости α, % | ||
| 0.75 | 0.87 | 0.37 | 0.47 | ||
| 0.71 | 0.83 | 0.36 | 0.46 | ||
| 0.67 | 0.80 | 0.36 | 0.46 | ||
| 0.63 | 0.77 | 0.35 | 0.45 | ||
| 0.60 | 0.74 | 0.33 | 0.42 | ||
| 0.58 | 0.71 | 0.30 | 0.39 | ||
| 0.55 | 0.68 | 0.29 | 0.37 | ||
| 0.53 | 0.66 | 0.27 | 0.35 | ||
| 0.51 | 0.64 | 0.25 | 0.33 | ||
| 0.50 | 0.62 | 0.23 | 0.30 | ||
| 0.48 | 0.61 | 0.22 | 0.28 | ||
| 0.47 | 0.59 | 0.21 | 0.27 | ||
| 0.46 | 0.58 | 0.20 | 0.25 | ||
| 0.44 | 0.56 | 0.17 | 0.23 | ||
| 0.43 | 0.55 | 0.16 | 0.21 | ||
| 0.42 | 0.54 | 0.14 | 0.18 | ||
| 0.41 | 0.53 | 0.11 | 0.15 | ||
| 0.40 | 0.52 | 0.10 | 0.13 | ||
| 0.40 | 0.51 | 0.09 | 0.12 | ||
| 0.39 | 0.50 | 0.07 | 0.10 | ||
| 0.38 | 0.49 | 0.06 | 0.09 | ||
| 0.37 | 0.48 | 0.06 | 0.09 | ||
| P | 0.05 | 0.01 | - | 0.05 | 0.01 |
Коэффициент корреляции оценивает линейную связь, точнее линейный компонент связи. Довольно условно выделяют слабую (r<0.5), среднюю (0.5<=r<0.7) и сильную r>=0.7 связь (Лакин, 1990).
Корреляционное отношение h
Для измерения нелинейной связи между Х и Y используют корреляционное отношение. Формулы для вычисления коэффициентов корреляционного отношения hxy и hyx здесь не рассматриваются. Корреляционное отношение всегда является величиной положительной, значения от 0 (отсутствие связи) до 1 (функциональная связь). Оно позволяет характеризовать любую форму корреляции – и линейную, и нелинейную. Чем более различаются r и h, тем в большей степени нелинейной является связь. Если h= r, связь линейная.
| <== предыдущая страница | | | следующая страница ==> |
| Краткая историческая справка | | | Коэффициент детерминации |
Дата добавления: 2014-07-19; просмотров: 562; Нарушение авторских прав

Мы поможем в написании ваших работ!