
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Турбулентное течение. Полуэмпирическая теория турбулентности
Язык 1С очень похож на Бейсик. В 1С все ключевые слова можно писать по-русски.
| Конструкция языка 1С | Примечание |
| Процедура РассчитатьНалог(Сотрудник, НекаяДата) КонецПроцедуры | Простая процедура. После слова КонецПроцедуры точка с запятой не нужна, потому что это не оператор, а операторная скобка |
| Функция РассчитатьНалог(Сотрудник, НекаяДата) Возврат Налог; КонецФункции | Функция должна обязательно возвращать результат. |
| Если Оклад > 10000 Тогда КонецЕсли; | Простое условие. После слова КонецЕсли должна быть точка с запятой, потому что так заканчивается оператор Если |
| Результат = ?(Оклад > 10000, "Нормально","Плохо"); | Сокращенное Если. |
| Если (Оклад > 10000) И (КодКатегории = 2) Тогда КонецЕсли; | В составном логическом выражении скобки обязательны! |
| Пока Номер <= 50 Цикл КонецЦикла; | Простой цикл Пока (цикл с неизвестным числом повторений). После слова КонецЦикла должна быть точка с запятой, потому что так заканчивается оператор Пока |
| Для Номер = 1 По 50 Цикл КонецЦикла; | Простой цикл Для (цикл с известным числом повторений). |
| Перейти ~метка; <...> ~метка: | Так оформляются метки и оператор безусловного перехода (GOTO). Чем меньше в вашей программе будет меток, тем лучше. |
| Пока <условие> Цикл Если <условие> Тогда ........Продолжить; КонецЕсли; КонецЦикла; | Оператор Продолжить передает управление в начало цикла. |
| Пока <условие> Цикл Если <условие> Тогда .........Прервать; КонецЕсли; КонецЦикла; | Оператор Прервать производит досрочный выход из цикла. Управление передается на операторы после цикла. |
| Перем Сотр; | Явное объявление переменной. |
| Номер = 1; | Переменные можно не объявлять явно. При первом присвоении значения создается новая переменная. |
| ФИО = Фамилия + " " + Имя + " " + Отчество; | Сложение строк (конкатенация) |
| НекаяДата = '01.01.2002'; | Переменная, которая хранит дату. |
| Перем глТекущийПользователь Экспорт; | Объявление глобальной переменной в Глобальном модуле. Такие переменные доступны в любом месте конфигурации. |
| Попытка а = 10 / 0; Исключение Предупреждение("Деление на ноль!"); КонецПопытки; | Обработка исключительных ситуаций. Если во время выполнения операторов между словами Попытка и Исключение произошла ошибка, то управление передается на операторы между словами Исключение и КонецПопытки Если ошибки не было, то управление передается на операторы после слова КонецПопытки. |
| //это комментарий | Так оформляются комментарии. |
| СпрСотр.ВыбратьЭлементы(); | Вызов метода объекта производится как обычно, через точку. |
И так, сегодня мы ознакомились с назначением языка «1С» и синтаксисом встроенного языка, рассмотрели виды программных модулей.
Вопросы, связанные с построением и видами запросов, рассмотрим на следующей лекции.
Использованная для подготовки лекции литература
1. Введение в конфигурирование в системе «1С: Предприятие 8». Основные объекты. Версия 8.2. Фирма «1С», Москва, ООО «1С-Учебный центр№3», 2010.
2. 1С: Предприятие 8.2. Руководство разработчика. Часть 1. Фирма «1С», Москва, ООО «1С-Учебный центр№3», 2009.
3. 1С: Предприятие 8.2. Руководство разработчика. Часть 2. Фирма «1С», Москва, ООО «1С-Учебный центр№3», 2009.
Доцент кафедры АСУ
Т.Авакян
Турбулентное течение. Полуэмпирическая теория турбулентности
Согласно теории устойчивости, устойчивой является система, амплитуда бесконечно малого возмущения, которой не растет.
Ламинарное течение является гидростатически устойчивым.
Неустойчивость приводит к пульсации величин параметров потока (скорости и давления). Обычно, изменение скорости и давления описывается распределением Гаусса, в котором наиболее вероятностным значением (математическим ожиданием)являются средние значения скорости и давления.
Таким образом, мгновенные значения скорости и давления носят вероятностный характер. Предложил выражать мгновенные значения параметров течения в виде линейной комбинации их среднего значения и пульсационной составляющей:
 +
+ 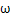 ’,
’,  - среднее значение параметра;
- среднее значение параметра; 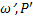 – пульсационная составляющая значения параметра
– пульсационная составляющая значения параметра
P= 
Правила осреднения, обозначаемого чертой над символом:
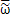 =
=  ,
,

 = 0
= 0
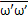
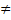 0
0
Вывод основного уравнения гидродинамики для турбулентного режима
(уравнения Рейнольдса)
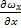 +
+  +
+ 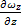 = 0 – уравнение неразрывности
= 0 – уравнение неразрывности
 +
+  +
+  = 0
= 0
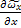 +
+ 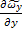 +
+ 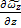 = 0 – уравнение неразрывности турбулентного течения
= 0 – уравнение неразрывности турбулентного течения
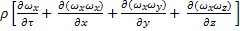 = -
= -  +
+ 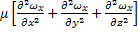
Уравнение Навье - Стокса
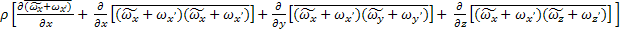 =
= 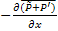 +
+ 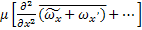
 +
+ 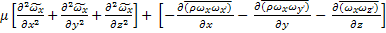
Приближение Буссинеска:
- 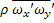
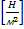 =
=  =
= 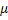 г
г 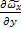
 -
- 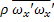
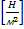 =
= 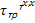 =
= 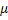 г
г 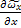 и т.д.
и т.д.
Тогда:
 =
= 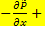 (
(  т)
т)  – Уравнение Рейнольдса в приближении Буссинеска.
– Уравнение Рейнольдса в приближении Буссинеска.
 =
= 
 -
- 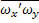 =
= 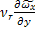
Параметры турбулентности:
L  – масштаб турбулентности – расстояние в потоке, на котором средняя скорость изменяется на величину пульсационной составляющей.
– масштаб турбулентности – расстояние в потоке, на котором средняя скорость изменяется на величину пульсационной составляющей.
L = 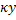 , константа Кармана
, константа Кармана  для крупномасштабных пульсаций
для крупномасштабных пульсаций
Изменение средней скорости на масштабе турбулентности 
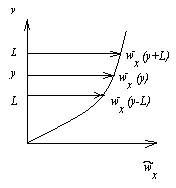
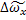 = 1/2
= 1/2  = L
= L 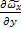 =
=  ,
,
Выражение получается взаимной подстановкой друг в друга приведенных ниже зависимостей.
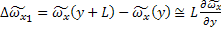 , так как разложение
, так как разложение 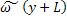 в ряд и ограничение его первым членом дает
в ряд и ограничение его первым членом дает
 L
L 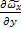
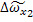 =
=  -
- 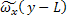
 L
L 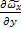 , так как разложение
, так как разложение  в ряд и ограничение его первым членом дает
в ряд и ограничение его первым членом дает
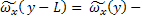 L
L 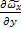 ,
,
ReL =  Rex =
Rex =  ,
,  - крупномасштабная пульсация, x мелкомасштабная пульсация и L
- крупномасштабная пульсация, x мелкомасштабная пульсация и L  , таким образом диссипирует энергию мелкомасштабной пульсаци, так как малый критерий Re- это большая сила трения, большая вязкость, а, следовательно, большая величина диссипированной энергии.
, таким образом диссипирует энергию мелкомасштабной пульсаци, так как малый критерий Re- это большая сила трения, большая вязкость, а, следовательно, большая величина диссипированной энергии.
На основе теории размерности можно получить выражение для турбулентной вязкости:
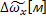 ; L
; L  ;
;  ;
;  – параметры потока, характеризующие течение:
– параметры потока, характеризующие течение:
 =
= 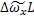 = L2
= L2 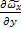 =
=  2y2
2y2 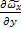
 т
т  =
= 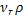 =
=  2y2
2y2 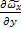
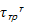 =
= 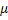 г
г 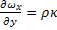 2y2
2y2 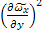
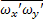 = -
= -  2y2
2y2 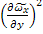
После определения значений 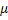 т и
т и  можно решать конкретные задачи с использованием уравнения Рейнольдса.
можно решать конкретные задачи с использованием уравнения Рейнольдса.
Определим профиль скоростей в плоском квазистационарном турбулентном потоке.
Определить профиль скоростей в плоском, квазистационарном, турбулентном потоке при безнапорном течении
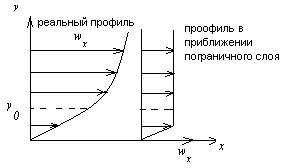 а) профиль скоростей, полученный решением уравнения Рейнольдса.
а) профиль скоростей, полученный решением уравнения Рейнольдса.
б)профиль скоростей в приближении пограничного слоя.
Из уравнения Рейнольдса при оговоренных условиях имеем:
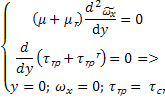
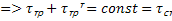
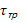 =
=  – слабо зависит от y.
– слабо зависит от y. 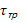 =
=  2
2 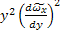 - пропорционально y2. Решаем методом асимптотического анализа со сращиванием полученных решений:
- пропорционально y2. Решаем методом асимптотического анализа со сращиванием полученных решений:
y 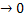 ;
; 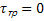 ;
; 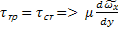 =
= 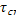
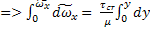
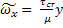 - линейная зависимость.
- линейная зависимость.
y 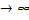 ;
;  2
2 
 Интегрируем и получаем:
Интегрируем и получаем:
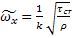 lny+С – логарифмический профиль скоростей в потоке вдали от стенки
lny+С – логарифмический профиль скоростей в потоке вдали от стенки
 =
=  – назовем, согласно размерности динамической скоростью
– назовем, согласно размерности динамической скоростью  *
*
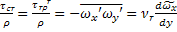 =
= 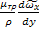
 =
= 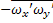
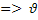 *=
*= 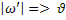 * - пульсационная составляющая и динамическая скорость – это одно и то же.
* - пульсационная составляющая и динамическая скорость – это одно и то же.
Re = 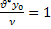 (при равном соотношении сил трения и инерции выбираем точку сращивания у, т.к. асимптотические решения получены для случаев превалирования силы трения (решение при у
(при равном соотношении сил трения и инерции выбираем точку сращивания у, т.к. асимптотические решения получены для случаев превалирования силы трения (решение при у  или силы инерции (решение при у
или силы инерции (решение при у  )
)
Координата сращивания равна:
у0= 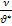
 у0=
у0=  =
= 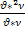 =
=  =
= 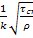 lny0+C
lny0+C 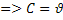 *-
*- 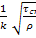 lny0
lny0
Важный вывод: скорость в точке сращивания равна пульсационной составляющей 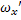 ,a
,a  - равна 0, что согласуется с гипотезой прилипания
- равна 0, что согласуется с гипотезой прилипания
 ln
ln  +
+  *=
*= 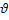 *
* 
Точное решение этой задачи имеет вид:
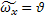 *
* 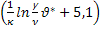
Полученные в результате решения уравнения Рейнольдса два различных вида профилей скоростей: линейного у стенки и логарифмического профиля скорости вдали от нее и вид соответствующих функций согласуется с гипотезой Прандтля о наличии в пристенной области пограничного слоя с иным, чем в ядре потока механизмом переноса количества движения.
| <== предыдущая страница | | | следующая страница ==> |
| Вопрос №3. Синтаксис языка 1С | | | Тема 8. Управление коммуникациями, конфликтами, стрессами |
Дата добавления: 2014-07-19; просмотров: 542; Нарушение авторских прав

Мы поможем в написании ваших работ!