Средняя арифметическая величина

Наиболее распространенным видом средних величин при обобщении социально – экономических явлений является средняя арифметическая величина, которая бывает простой и взвешенной.

Средняя арифметическая простая применяется в том случае, когда по каждой единице совокупности известна величина изучаемого признака, выраженная абсолютным, объемным показателем.

Х_ср. =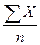

Здесь, Х – индивидуальные значения признака у отдельных единиц совокупности;

n – число единиц в совокупности.

Например, в домохозяйстве 5 человек: отец, заработная плата его составляет 4 800 руб., мать с заработной платой 2 100, заработная плата зятя составляет 3 600, стипендия дочери 880 руб., бабушка с пенсией 1 400 руб., других источников дохода нет. Тогда средний месячный доход на одного члена домохозяйства составит: 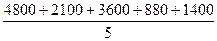= 2556 руб.

Если же исходные данные сгруппированы и в каждой группе известны величины группировочных признаков и число единиц, то применяется средняя арифметическая взвешенная.

Х_ср. =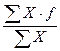

где, Х – значение изучаемого признака в группе;

f – частота, т.е. число единиц изучаемого признака в группе.

Например, по результатам экзамена по теории статистики известно, что в академической группе, состоящей из 25 студентов, было получено отличных оценок – 4, хороших – 9, удовлетворительных – 10 и неудовлетворительных – 2, тогда средний балл составит 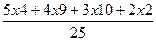= = 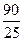3,6

Известны математические свойства средней арифметической взвешенной, позволяющие вместо частот применять частости, т.е. относительные величины структуры и координации.

Свойство: если в формуле средней арифметической взвешенной величины каждую частоту умножить и (или) разделить на одно и тоже число, то значение средней величины не изменится.

Действительно, вспомним, что относительная величина структуры выражается удельным весом, который обозначают d.

d = .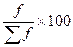

В этой формуле Σf для данной совокупности – величина постоянная.

Относительная величина координации имеет вид .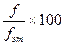

Здесь, f – число единиц в каждой группе;

f_эт.- число единиц в группе, выбранной за эталон.

В этой формуле f_эт для данной совокупности – величина постоянная

Примеры смотрите дальше, в методических рекомендациях по применению формул средних величин.

При расчете системных средних в каждой группе приводится среднее значение группировочного признака и число единиц, расчетная формула таже.

Дата добавления: 2014-07-19; просмотров: 289; Нарушение авторских прав

Мы поможем в написании ваших работ!