Средняя гармоническая величина

Напомним, что каким бы видом средних величин мы не пользовались, необходимо соблюдение условия (1).

Если исходные данные сгруппированы, величина изучаемого признака выражена абсолютным качественным показателем и, кроме того, по каждой единице совокупности объем явления одинаков, то в расчете применяется средняя гармоническая простая.

Х_ср. =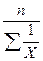

В этой формуле обозначения те же, что и в формуле средней арифметической простой.

Показатель называется объемным, если он характеризует величину изучаемого признака по совокупности, объемные показатели получают в ходе регистрации фактов. Например, объем товарооборота, объем товарных запасов, фонд заработной платы, затраты на производство продукции, валовой урожай и др.

Показатель называется качественным, если он рассчитан на единицу совокупности, т.е. качественный показатель получается расчетным путем (по формуле (1)). Например, себестоимость единицы продукции, средняя цена за единицу продукции, средняя заработная плата одного работника и т.д.

Рассмотрим простой пример.

В магазине работают два продавца, причем один из них затрачивает на обслуживание одного покупателя 3 мин., а другой 5 мин. Нужно определить среднее время, в течение которого обслуживается один покупатель.

Типичный ход решения. На обслуживание одного покупателя в среднем затрачивается (3 + 5)/2 = 4 мин., т.е. в расчете была применена формула средней арифметической простой.

Проверим, насколько расчетные данные соответствуют фактическим данным. Итак, расчетные данные показывают, что один «средний статистический продавец» за один час обслужит 60 : 4 = 15 покупателей. За 8 часов будет обслужено 8 х 15 = 120 покупателей, а два «средних статистических» продавца за 8 часов обслужат 120 х 2 = 240 покупателей.

Фактически первый продавец может обслужить за один час 60 : 3 = 20 покупателей, а второй 60 : 5 = 12 покупателей. Таким образом, за один час работы два продавца обслуживают 20 + 12 = 32 покупателя. Тогда за 8 часов они обслужат 8 х 32 = 256 покупателей.

В итоге получили, что расчетные данные не совпадают с фактическими данными.

Проверим алгоритм расчетов. Вначале установим сущность показателя.

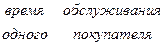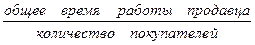= (3)

Изучаемый признак, «время обслуживания одного покупателя», является качественным, а не объемным, кроме того, покупатели сгруппированы, так как каждый обслуживается только у одного продавца.

Введем условные обозначения: В – время обслуживания одного покупателя; ОВ – общее время работы продавца; К – количество покупателей.

Тогда формула (3) примет вид: В = 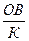. При расчете для двух продавцов необходимо сохранить сущность показателя, то есть В_ср = (4). Поскольку о количестве продавцов ничего не известно, выразим его из формулы (3), то есть получаем, что К = 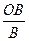. Затем подставляем это выражение в формулу (4) и получаем В_ср = 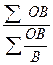, то есть среднюю гармоническую взвешенную. Однако, продолжительность работы каждого продавца одинакова, то есть ОВ – величина постоянная, то можно вынести ее за знак суммы. Получаем В_ср = 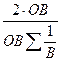= 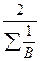, то есть окончательно получили формулу средней гармонической простой, где n =2 продавцам. В_ср = 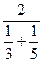= = 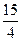3,75 мин.

Снова проверим соответствие расчетных данных фактическим данным.

За один час работы «средний статистический продавец» может обслужить 60 : 15/4 = 16 покупателей, а за 8 часов 8 х 16 = 128 покупателей. Работая вместе, они обслуживают 128 х 2 = 256 покупателей. Таким образом, получили соответствие расчетных данных фактическим.

Если исходные данные сгруппированы и в каждой группе, кроме величины группировочного признака (Х), известен объем изучаемого явления (W), то расчеты среднего значения признака выполняются по формуле средней гармонической взвешенной.

Х_ср. = /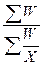

При решении задач часто применяется математическое свойство средней гармонической взвешенной. Если каждое значение (W) умножить и (или) разделить на одно и то же число, то среднее значение признака не изменится. Это позволяет вместо абсолютных, объемных показателей, какими являются объемы явления по совокупности (W), применять их удельные веса или относительные величины координации. Примеры смотрите в методических рекомендациях по применению формул средних величин.

Дата добавления: 2014-07-19; просмотров: 433; Нарушение авторских прав

Мы поможем в написании ваших работ!