
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОЦЕНКИ ТОЧНОСТИ РАЗНОСТНЫХ СХЕМ ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Для линейных задач оценки погрешности, как априорные мажорантные, так и апостериорные ассимтотические, можно получить на основании приведенных ниже теорем.
Теорема 1. Если условия теоремы о сходимости выполнены, (т.е. если решение задачи cуществует, разностная схема корректна и аппроксимирует дифференциальную задачу на данном решении, то разностное решение сходится к точному), операторы 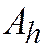 и
и 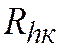 линейные, а порядок аппроксимации равен р, то сходимость имеет порядок не ниже р. (Ее кратко формулируют так: «Для линейных схем порядок точности не ниже порядка аппроксимации»).
линейные, а порядок аппроксимации равен р, то сходимость имеет порядок не ниже р. (Ее кратко формулируют так: «Для линейных схем порядок точности не ниже порядка аппроксимации»).
Доказательство. Пусть дифференциальная задача
Au = f , 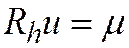 (31.1)
(31.1)
и разностная схема
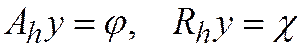 (31.2)
(31.2)
линейны, а граница Г состоит из кусков Гк (к = = 1, 2, …, K). Условие устойчивости 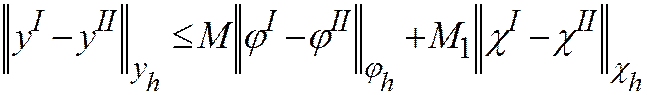 для линейной схемы принимает вид
для линейной схемы принимает вид 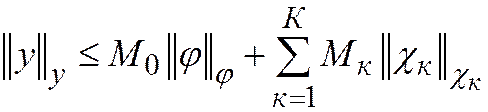 (31.3)
(31.3)
(начальные условия, если задача их содержит, входят в сумму по граничным условиям). Рассмотрим погрешность разностного решения 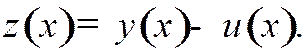
Вычтем соотношение 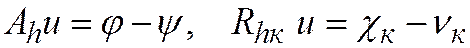 (31.4)
(31.4)
из разностной схемы (31.2) и заметим, что благодаря линейности схемы
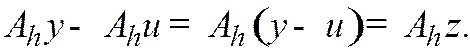
Тогда z(x) удовлетворяет схеме с разностными операторами (31.2) 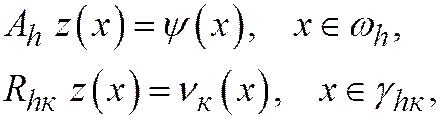 (31.5)
(31.5)
где в правых частях стоят невязки. Применяя к (31.5) условие устойчивости (31.3), получим
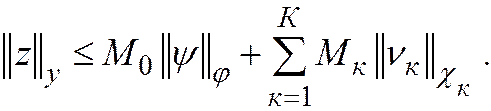 (31.6)
(31.6)
Поскольку схема (31.2) имеет порядок аппроксимации р, то
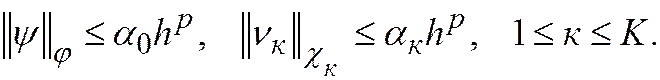
Подставляя эти выражения в (31.6), получим априорную мажорантную оценку погрешности
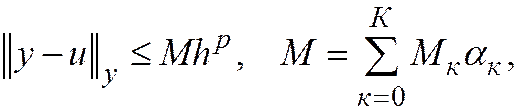
что и доказывает теорему.
Замечание 1. Для доказательства требовалась линейность только разностных операторов, но фактически линейными разностными операторами можно аппроксимировать только линейные дифференциальные или интегральные операторы.
Замечание 2. Если условия теоремы 1 настоящей лекции выполнены, то порядок точности может быть выше порядка аппроксимации. В таких случаях более полное исследование задачи нередко показывает, что для сходимости в данной норме 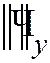 достаточно устойчивости по более слабой норме
достаточно устойчивости по более слабой норме 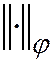 , в которой порядок аппроксимации выше.
, в которой порядок аппроксимации выше.
Замечание 3. Для случая многих переменных порядок аппроксимации по разным переменным может быть неодинаковым. Очевидно, порядок точности по разным переменным также может быть различным.
Пример. Явная схема для первой краевой задачи теплопроводности, разобранная ранее, имеет погрешность аппроксимации
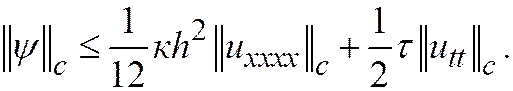
Начальные данные и краевые условия аппроксимируются точно, и устойчивости по ним можно не требовать. Условие устойчивости по правой части имеет вид 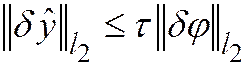 или
или 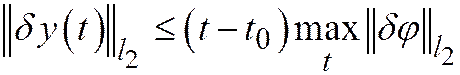 .
.
Отсюда следует априорная оценка т.е. схема имеет первый порядок точности по времени и второй – по пространству.
Для практических вычислений важное значение имеет следующая теорема 2.
Теорема 2. Пусть задача (31.1) и разностная схема (31.2) линейны, разностная схема корректна и аппроксимирует задачу так, что существует
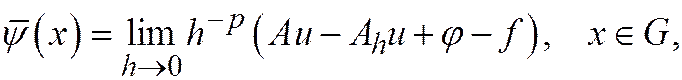
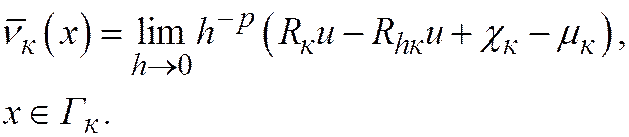
Пусть существует решение 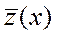 задачи
задачи
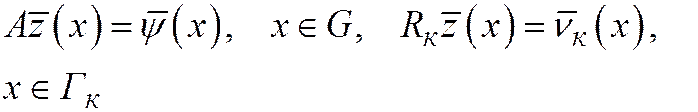 и на этом решении разностные операторы
и на этом решении разностные операторы 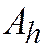 ,
, 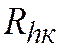 , аппроксимируют дифференциальные операторы
, аппроксимируют дифференциальные операторы 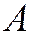 ,
, 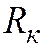 тогда погрешность разностного решения (31.2) имеет следующую асимптотику
тогда погрешность разностного решения (31.2) имеет следующую асимптотику 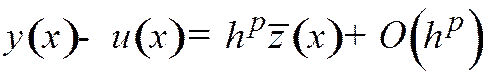 при
при 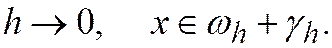
Доказательство. Пользуясь линейностью операторов, нетрудно установить следующее равенство
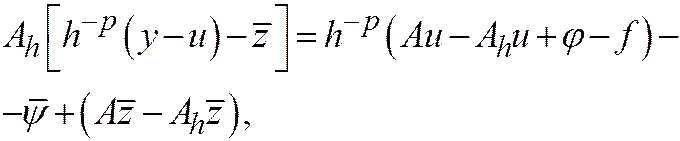
аналогичные равенства записываются для граничных условий. При 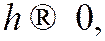 правые части всех этих равенств стремятся по норме к нулю: последняя скобка на основании предположения об аппроксимации на функции
правые части всех этих равенств стремятся по норме к нулю: последняя скобка на основании предположения об аппроксимации на функции 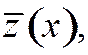 а остальные члены – согласно условию теоремы.
а остальные члены – согласно условию теоремы.
Тогда, благодаря устойчивости разностных операторов 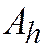 ,
, 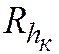 , выражение в квадратных скобках в левой части этих равенств стремится по норме к решению задачи (31.2) с нулевой правой частью, а оно тождественно равно нулю. Уравнение линейное, начальные и граничные равны нулю. Теорема доказана.
, выражение в квадратных скобках в левой части этих равенств стремится по норме к решению задачи (31.2) с нулевой правой частью, а оно тождественно равно нулю. Уравнение линейное, начальные и граничные равны нулю. Теорема доказана.
Замечание 1. Теорему можно обобщить на случай многих переменных, даже если порядок аппроксимации по разным переменным неодинаковый. В случае двух переменных возможна следующая асимптотика погрешности
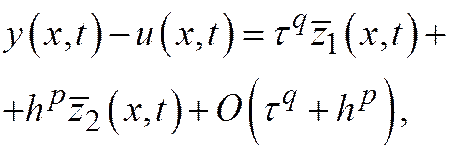
или иная в зависимости от характера аппроксимации.
Изложенная в этой главе теория разностных схем применима к разностным схемам, аппроксимирующим корректно поставленные задачи для обыкновенных дифференциальных уравнений, уравнений в частных производных и интегральных уравнений. Хотя в большинстве формулировок фигурировало только одно уравнение и одна переменная, но теория очевидным образом обобщается на системы уравнений или случай многих переменных.
Теория разностных схем применяется также для доказательства существования решения точной задачи (31.7) и установления его свойств. В качестве примера приведем без доказательства одно утверждение.
Теорема 3. Если для дифференциальной задачи (31.1) существует хотя бы одна корректная разностная схема 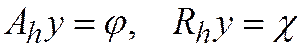 , (31.2) аппроксимирующая задачу на функциях
, (31.2) аппроксимирующая задачу на функциях 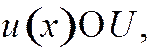 то решение u(x) дифференциальные задачи (31.1) в классе U существует и единственно. Если правые части
то решение u(x) дифференциальные задачи (31.1) в классе U существует и единственно. Если правые части 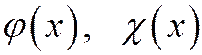 непрерывны равномерно по h, то
непрерывны равномерно по h, то 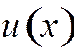 непрерывно зависит от
непрерывно зависит от 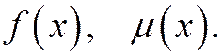
| <== предыдущая страница | | | следующая страница ==> |
| Метод разделения переменных исследования устойчивости разностных схем | | | Сравнение разностных схем на тестах |
Дата добавления: 2014-07-30; просмотров: 342; Нарушение авторских прав

Мы поможем в написании ваших работ!