Примеры задач оптимизации в проектировании ЭВС

Пример 1. Определение параметров технологического процесса.

Прочность соединений при пайке волной припоя зависит от четырех параметров:

- температура припоя;

- скорость движения печатной платы относительно припоя;

- угол наклона печатной платы относительно припоя;

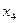- высота волны припоя (скорость фонтанирования).

На основе экспериментальных исследований технического процесса получена зависимость необходимой выходной характеристики технического процесса от указанных параметров. Она выражается следующей функцией:

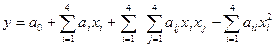, где 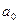, , 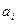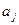- некоторые коэффициенты, являющиеся постоянными величинами.

Требуется определить оптимальные значения параметров техпроцесса 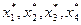в области 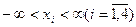, при которых выходная характеристика у достигает экстремальное значение.

Пример 2. Определение допусков на параметры изделия (объекта).

Пусть выходные характеристики конструкции связанны с внутренними параметрами некоторыми зависимостям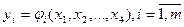и или .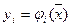

Внутренние параметры 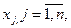могут изменяться в известных пределах, указанных в т3 или другой документации: 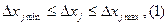, где j- номер параметра.

Отклонение любой выходной характеристики от номинального значения определяется как

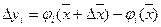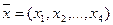, где и .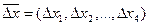

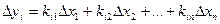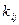Раскрывая эту формулу в итоге можно получить , где - коэффициент влияния j- ого параметра 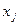на i- ую выходную характеристику .

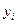Отсюда искомый вектор 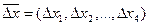определяется следующей системой неравенств:

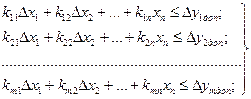(2),

где 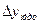- предельно возможные значения выходных характеристик.

Оптимальность выбора вектора допусков 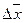может быть задана показателем качества

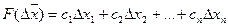, (3)

где коэффициенты 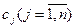могут учитывать влияние соответствующих параметров на стоимость, надежность, потребляемую мощность или габариты конструкции.

Тогда, задача выбора рациональной системы допусков конструкции сводится к поиску экстремума целевой функции (3) при ограничениях (1) и (2).

Пример 3. Планирование промышленных технологий.

Промышленное предприятие может использовать для производства одного вида изделий n различных технологий и m видов необходимых ресурсов (материалы, заготовки, трудовые затраты, энергия, оборудование и т. п.). запас каждого вида ресурсов ограничен и составляет величину .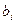

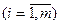При использовании некоторой j- ой технологии 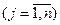в единицу времени расходуется 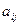единицу ресурса i- ого вида и в результате производится 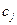изделий.

Требуется определить план производства, т. е. время использования технологии каждого вида (и количество произведенных изделий), чтобы при наличных ресурсах выпустить максимальное число изделий.

Обозначим через 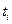время, в течении которого изделия выпускаются по j- ой технологии. Выпуск изделий за это время составит 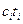штук, а израсходовано будет 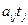единиц i- ого ресурса .

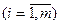Общее потребление каждого j-ого ресурса всеми технологическими процессами 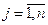не должно превышать величины 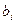, т. е.

.

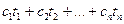Требуется найти

,

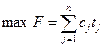при ограничениях

.

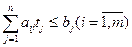
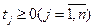Пример 4. Задача о раскрое листового материала.

Листовой материал ( металл, текстолит, гетинакс…) поступает на предприятие в виде листов стандартного размера (или нескольких размеров), из которых затем вырезают заготовки или готовые детали необходимого вида. При раскрое каждого листа все остатки идут в отходы. Имеется m различных видов заготовок или деталей, причем всего требуется 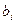деталей каждого вида .

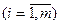Лист материала можно раскроить одним из n возможных вариантов. Для каждого j-ого варианта 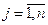известно: число 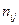получаемых деталей каждого i- ого вида и величина 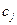отходов материала .

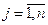Требуется составить оптимальный план раскроя материала, т. е. определить сколько листов кроить по каждому варианту, чтобы получить необходимое число деталей каждого вида при минимальных суммарных отходах.

Обозначим через 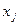количество листов для j-ого варианта раскроя. Тогда вектор 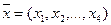представляет некоторый план раскроя. Чтобы этот план был допустимым, необходимо получение каждой i- ой детали в количестве, не меньшем .

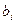Тогда задачу можно сформулировать следующим образом. Определить вектор 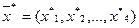, удовлетворяющей условием:

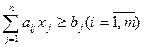
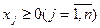
для которого минимизируется суммарное количество отходов

.

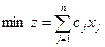Замечание: задача существенно усложняется, если требуется использовать целое количество листов (т. е. 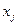- целые числа) или листы могут иметь различный размер.

Дата добавления: 2014-08-04; просмотров: 315; Нарушение авторских прав

Мы поможем в написании ваших работ!