Классификация задач оптимизации

1. По наличию ограничений.

Если область допустимых решений 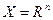, то задача не является задачей оптимизации без ограничений или задачей безусловной оптимизации. При этом для характеристики экстремума целевой функции используют термин «безусловный».

Если 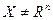, то имеет место задача оптимизации с ограничениями или задача условной оптимизации. При этом говорят об «условном экстремуме», а множество допустимых решений ограничивается системой уравнений вида 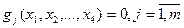или системой неравенств .

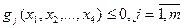2. По количеству управляющих параметров 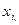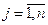, принадлежащих множеству допустимых решений - при n=1 задача одномерной оптимизации.

Здесь поиск экстремума целевой функции производится на некоторой кривой в интервале 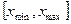, т. е. 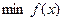, 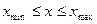или 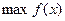, 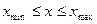- при n>1 задача многопараметрической или многомерной оптимизации. Здесь производится поиск экстремума функции 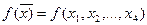, определяемой на некотором множестве допустимых решений 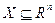, т. е. 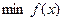, 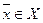или , .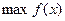

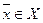3. По количеству экстремумов целевой функции различают задачи унимодальной (одноэкстремальной ) и многоэкстремальной оптимизации.

Поясним эти понятия. В зависимости от вида целевой функции 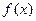оптимальное решение 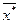может быть точкой локального или глобального минимума (максимума).

Вектор 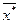называется точкой локального (относительного) минимума, если для всех точек 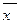, принадлежащих 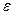- окрестност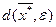и точки 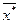, функция 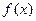не принимает меньшего значения:

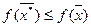для всех .

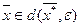Замечание: 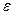- окрестностью точки 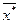называется множество точек вида: 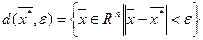, где расстояние между точками евклидова пространства:

.

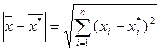Вектор 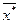является точкой глобального (абсолютного) минимума, если ни в какой другой точке 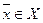допустимой области функция не принимает меньшего значения:

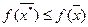для всех .

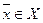Таким образом, глобальный минимум- это наименьший из всех локальных минимумов.

Например:

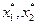- точки локального минимума,

- точка глобального минимума.

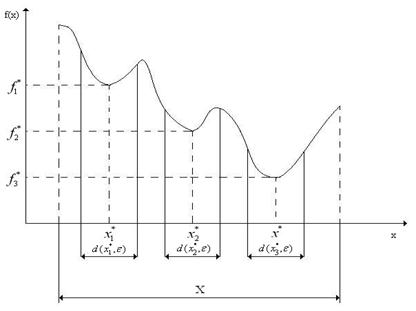
Понятия локального и глобального максимума выводятся аналогично.

Задачей унимодальной оптимизации является задача оптимизации вида 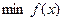, 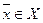или 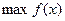, , 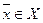для которой целевая функция имеет в области Х единственный локальный экстремум.

Если целевая функция имеет несколько локальных экстремумов, то это многозадачная задача оптимизации.

4. По количеству критериев оптимизации.

Различают задачи однокритериальной и многокритериальной (векторной) оптимизации.

В первом случае целевая функция единственна и имеет скалярный характер, во втором случае для совместного учета совокупности частных критериев 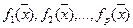обычно вводится векторный критерий оптимальности.

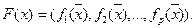
При этом минимизация 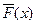эквивалентна одновременной минимизации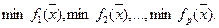

Поскольку частные критерии носят противоречивый характер, то оптимальное решение 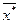задачи векторной оптимизации в общем случае не является оптимальным ни для одного из частных критериев, но должно быть компромиссным для векторного критерия в целом.

Возможным подходом к поиску компромиссного решения задачи векторной оптимизации является ее сведение к задаче многопараметрической оптимизации с единственной целевой функцией, учитывающей влияние всех частных критериев на решение.

Дата добавления: 2014-08-04; просмотров: 416; Нарушение авторских прав

Мы поможем в написании ваших работ!