
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выбор критериев оптимизации
Целевая функция в задаче оптимизации обязательно должна быть скалярной, т. е. оптимизация конструкции или технологического процесса может выполняться только по одному критерию.
Однако задачи конструкторско- технологического проектирования обычно носят многоцелевой характер, т. е. имеется большое число частных показателей, характеризующих качество проекта (надежность, стоимость, быстродействие, потребляемая мощность и т. д.)
Поэтому обоснованный выбор критериев оптимизации представляет важную задачу. Рассмотрим математические методы
, позволяющие учитывать многоцелевой характер задач оптимизации. Все эти методы выполняют свертывание векторного критерия в скалярный.
1. Метод обобщенного критерия.
Пусть имеется совокупность частных критериев качества 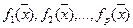 ,
, 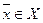 .
.
На ее основе вводится скалярная функция от частных показателей вида 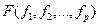 .
.
Если все показатели 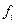 измеряются по одной шкале, то возможно использовать аддитивный или мультипликативный критерий:
измеряются по одной шкале, то возможно использовать аддитивный или мультипликативный критерий:
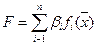 - аддитивный,
- аддитивный,
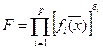 - мультипликативный,
- мультипликативный,
где 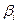 - вес (степень влияния) соответствующего критерия, устанавливаемый, например, в результате экспертных оценок.
- вес (степень влияния) соответствующего критерия, устанавливаемый, например, в результате экспертных оценок.
После формирования обобщенного критерия задача оптимизации ставится как 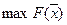 ,
, 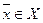 или
или 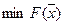 ,
, 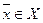 .
.
Если частные показатели качества 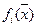 измеряются по разным шкалам, то формируется обобщенный критерий, приведенный к единой шкале измерений (для случая
измеряются по разным шкалам, то формируется обобщенный критерий, приведенный к единой шкале измерений (для случая 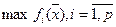 ):
):
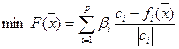 , где
, где 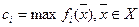 .
.
Для такого критерия решение задачи минимизации 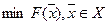 обеспечивает максимизацию всех частных критериев, т. к. функция
обеспечивает максимизацию всех частных критериев, т. к. функция 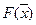 задает относительные отклонения частных критериев от их максимально- возможных значений
задает относительные отклонения частных критериев от их максимально- возможных значений 
Основной недостаток такого метода выбора критерия оптимизации заключается в субъективном определении значений 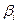 , что может привести к улучшению одних частных показателей за счет ухудшения других.
, что может привести к улучшению одних частных показателей за счет ухудшения других.
2. Метод главного критерия.
Предполагается, что среди всех частных показателей можно выделить один, наиболее важный, который определяется обычно показателем ЭВС. Например, для бортовой аппаратуры - это надежность, для суперЭВМ- быстродействие, для микроЭВМ- стоимость и т. д.
Остальные частные критерии выступают в роли ограничений, т. е. Их значения не должны быть больше или меньше их предельно-допустимых значений.
Математически задача оптимизации формулируется следующим образом: найти 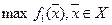 при ограничениях
при ограничениях 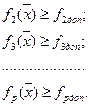
Такая задача оптимизации всегда корректна и является наиболее распространенной. Она называется однокритериальной задачей оптимизации.
3. Метод минимального (максимального) критерия.
В качестве функции 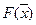 выбирается худшее значение из частных критериев и решается задача максимизации, т. е.
выбирается худшее значение из частных критериев и решается задача максимизации, т. е. 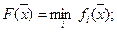
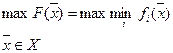 - максимальный критерий.
- максимальный критерий.
Другими словами, для нескольких максимизируемых параметров выбирается наихудший, который должен быть максимальным.
Для максимального критерия наоборот- минимизируется наибольшее значение из всех частных показателей: 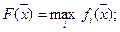
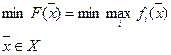 .
.
4. Метод последовательных уступок.
Используется в том случае, если нельзя выделить главный критерий, но можно некоторым образом упорядочить показатели по степени их важности.
Предположим, что частные критерии  расположены по убыванию важности.
расположены по убыванию важности.
Тогда сначала решается задача 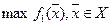 ; результат которой обозначается через
; результат которой обозначается через  .
.
Затем вводится некоторая уступка (ухудшение) 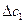 в первом показателе и решается задача
в первом показателе и решается задача 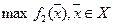 при ограничении (дополнительном)
при ограничении (дополнительном) 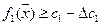 .
.
Максимальное значение показателя 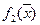 обозначаем через
обозначаем через 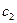 и назначаем уступку
и назначаем уступку 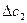 Решаем задачу:
Решаем задачу:
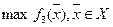 при дополнительных ограничениях
при дополнительных ограничениях 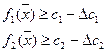 .
.
Процесс продолжается для всех p критериев качества.
Окончательный вариант решения находится как 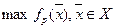 при ограничениях
при ограничениях 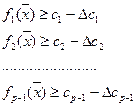 .
.
Сложность данного метода заключается в выборе значений 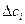 , а также в определении степени важности критериев качества (порядка их следования при решении).
, а также в определении степени важности критериев качества (порядка их следования при решении).
В качестве выводов укажем способы выбора критериев при автоматизированном проектировании ЭВС.
1. Если в т3 на проектирование сформулировано условие, что необходимо оптимизировать один из параметров проектируемого объекта при соблюдении ограничений на остальные параметры, то необходимо использовать метод главного критерия.
2. При наличии в т3 нескольких критериев оптимальности выбор аддитивного критерия целесообразен в тех случаях, когда существенные значения имеют абсолютные значения частных критериев при выбранном векторе решения 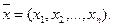
3. Если существенное значение имеет взаимное изменение абсолютных значений критериев при вариации вектора 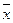 , то в этом случае рекомендуется применять мультипликативный критерий оптимизации.
, то в этом случае рекомендуется применять мультипликативный критерий оптимизации.
4. Если задача предполагает достижение примерного равенства конфликтующих частных критериев, то оптимальное проектирование следует проводить по минимаксному или максиминному критерию.
5. Способы вычисления весовых коэффициентов, учитывающих важность частных критериев.
В многокритериальных задачах возникает необходимость объективной оценки важности частных критериев, включаемых в аддитивный, мультипликативный или минимаксный критерий оптимальности.
Наибольшее распространение для этого получили методы экспертных оценок. Рассмотрим основные из них - ранжирования и метод приписывания балов.
1. Метод ранжирования.
Экспертиза проводится группой из l экспертов. Каждого эксперта просят расставить частные критерии 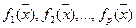 в порядке их важности: первый - наиболее важный критерий, второй - следующий по важности и т. д.
в порядке их важности: первый - наиболее важный критерий, второй - следующий по важности и т. д.
Затем критериям присваиваются ранги:
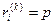 - для наиболее важного критерия,
- для наиболее важного критерия,
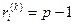 - для следующего,
- для следующего,
………….
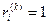 - для наименее важного,
- для наименее важного,
где I- номер критерия, k- номер эксперта.
Отсюда весовые коэффициенты:
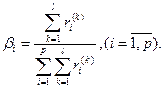
2. Метод приписывания баллов.
Эксперты оценивают важность частного критерия по шкале 0-10. разрешается оценивать дробными величинами или приписывать одну величину нескольким критериям.
Пусть 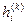 - балл i- ого критерия у k- ого эксперта. Отсюда вычисляется величина, показывающая относительную важность этого критерия у k- ого эксперта (вес критерия).
- балл i- ого критерия у k- ого эксперта. Отсюда вычисляется величина, показывающая относительную важность этого критерия у k- ого эксперта (вес критерия).
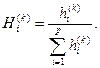
Затем определяем весовые коэффициенты:
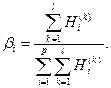
| <== предыдущая страница | | | следующая страница ==> |
| Классификация задач оптимизации | | | Линейное программирование |
Дата добавления: 2014-08-04; просмотров: 588; Нарушение авторских прав

Мы поможем в написании ваших работ!