Обнаружение и исключение ошибки

В системах могут происходить сбои, отсюда аппаратура работает не стабильно. При однократном измерении ошибки выявляются только анализом. При многократном измерении одной и той же величины результат отдельных измерений значительно отличается от других. Иногда ошибка очевидна и следует проанализировать и исключить. Если отличие незначительно, то оно может быть ошибочно, как и рассеивание. Поэтому нужно правило принятия решения. После того как все влияющие факторы учтены и все поправки внесены, центральная предельная теорема теории вероятностей утверждает, что результат измерения при этом подчиняются так называемым нормальным законам.

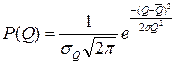
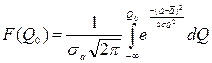
Если условия выполняются, то весь массив экспериментальных данных при многократном измерении включение одного и того же размера должно группироваться около среднего значения, а выпадение какого-либо результата из этого массива говорит, что он ошибочный.

Найдём вероятность, которой любое значение результата подчиняющееся нормальному закону должно находится в интервале от Q₁ до Q₂.

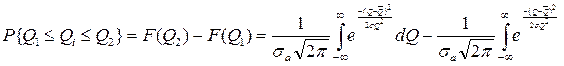
Интегралы в этом выражении не могут быть выражены через элементарные функции, более того для интегрирования нормального закона нет таблиц.

; ; ; ;

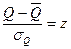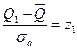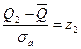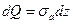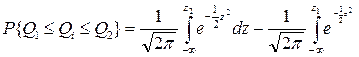
Интересующая нас вероятность выражена через разницу значений интегральных функций соответствует вероятности:

Дифференциал интегральной функции выглядит следующим образом:

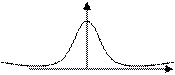P(z)

P(z) 1-------

0,5

z z

F(z)=1-F(-z)

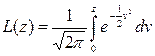
F(z)=1/2+L(z).

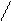
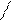
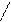
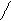
P(V) L(z)

L(z) 0,5------------

Если выбрать Z₂=-Z₁ и обозначить эту величину

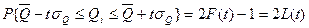
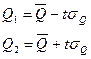
P

t

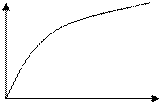
Параметр t играет важную роль. Он показывает на сколько s_Q с заданной вероятностью может отличаться от отдельного значения результата измерения подчиняется нормальному закону от своего определённого значения.

c P=0,5 на ±2/3s_Q; c P=0,68 на ±s_Q; c P=0,95 на ±2s_Q; с P=0,99на ±2,6s_Q; с P0,37 на ±3s_Q

Доверительный интервал .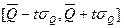

Его границы – доверительные границы с очень высокой вероятностью 0,997 все значения результата измерения подчиняющееся нормальному закону должны группироваться в пределах доверительного интервала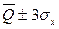

На этом основании сформулировано правило:

Если при многократном измерении одной и той же величины постоянного размера, сомнительное значения результата измерений отличающиеся от среднего больше чем на 3s_Q, то с вероятностью 0,997 оно является ошибочным и его следует отбросить. Это правило называется правилом 3-х сигм.

Дата добавления: 2014-08-04; просмотров: 436; Нарушение авторских прав

Мы поможем в написании ваших работ!