
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Проверка нормальности закона распределения вероятности результата измерения
При обработке экспериментальных данных возникает вопрос: подчиняются ли результаты измерения закону распределения? Не противоречивость данной гипотезы должна быть проверена. Поскольку ошибки искажают эмпирический закон, проверку на нормальность проводят после исключения ошибок.
Правдоподобна или нет гипотеза о нормальности закона распределения можно определить по виду гистограмм, построенных по результатам экспериментальных данных.
Порядок построения:
1) Интервалы 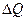 , на которые разбивается ось абсцисс следует брать по возможности одинаковыми.
, на которые разбивается ось абсцисс следует брать по возможности одинаковыми.
2) Число интервалов k устанавливают из следующей рекомендации.
| Число измерений | Рекомендуемое число интервалов |
| 40-100 | 7-9 |
| 100-500 | 8-12 |
| 500-1000 | 10-16 |
| 1000-10000 | 12-22 |
3) Масштаб гистограмм выбирают так, чтобы ее высота относилась к основанию как 5:8.
Если гистограмма имеет вид:
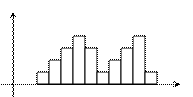
| то можно сказать, что не подчиняется закону |
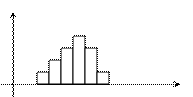
| то может и подчиняется |
А если вид обычный, то возникает сомнение, для решения которого нужно правило.
Существует несколько критериев согласия, по которым проверяются гипотезы о соответствии экспериментальных данных тому или иному закону распределения вероятностей.
Наиболее распространенный критерий Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения принимается сумма квадратов отклонений частностей 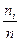 от теоретической вероятности
от теоретической вероятности 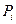 попадания отдельного значения результата измерения в
попадания отдельного значения результата измерения в 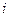 -ый интервал, причем каждое слагаемое берется с коэффициентом
-ый интервал, причем каждое слагаемое берется с коэффициентом 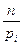 .
.

Если расхождение случайно, то 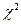 подчиняется
подчиняется 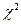 распределению Пирсона.
распределению Пирсона.
Кривые распределения:
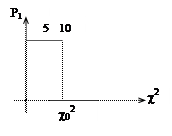
Задавшись значением интервальной функции распределения Пирсона 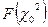 можно проверить боле или меньше ее аргумента
можно проверить боле или меньше ее аргумента 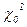 вычисленное значение
вычисленное значение 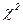 .
.
Пример
100 независимых численных значений результата измерений напряжения цифровым вольтметром, каждая из которых проводилась 1 раз приведены в 1-ой графе.
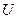
| 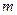
| 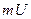
| 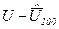
| 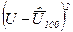
|
| 8,30 | ||||
| … | … | |||
| 8,95 |
Проверить гипотезу о том, что результаты измерения подчиняются нормальному закону.
Решение:
1.Используя результаты вспомогательных вычислений, сведенные к 3-ей графе, найдем среднее арифметическое.
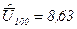
2. Используя 5 и 6 графы определим стандартное отклонение 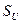 =0,127.
=0,127.
3.Ни одно из значений не отличается от среднего больше чем на 3 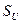 =0,381. Следовательно, ошибок нет.
=0,381. Следовательно, ошибок нет.
4.При использовании критерия Пирсона в каждом интервале должно быть не меньше 5 независимых значений, в соответствии с этим интервалы будут такими:
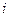
| Интервалы | 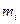
| 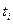
| 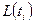
| 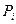
| 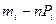
| 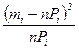
| |
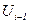
| 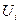
| |||||||
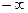
| 8,425 | -1,614 | -0,4767 | 0,0533 | ||||
| 8,425 | 8,475 | -1,220 | -0,3888 | 0,0579 | ||||
| 8,475 | 8,525 | -0,827 | -0,2959 | 0,0929 | ||||
| 8,525 | 8,575 | -0,433 | -0,1676 | |||||
| 8,575 | 8,625 | -0,039 | -0,0157 | |||||
| … | ||||||||
| 8,825 | 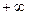
| 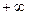
| 0,5000 | 0,0623 |
5. Определим на сколько 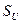 отстоит от среднего арифметического, правая граница
отстоит от среднего арифметического, правая граница 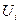 каждого интервала
каждого интервала 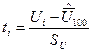
6. По значению 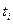 из графика можно определить с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения попадает в интервал
из графика можно определить с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения попадает в интервал 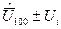 . С вероятностью в 2 раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность определяется функцией Лапласа
. С вероятностью в 2 раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность определяется функцией Лапласа 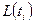 . Так что для повышения точности можно воспользоваться не графиком, а таблицей. Данные из таблиц занесем в графу
. Так что для повышения точности можно воспользоваться не графиком, а таблицей. Данные из таблиц занесем в графу 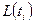 .
.
7. Теоретическая вероятность 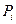 попадания в
попадания в 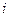 -ый интервал отдельного значения результата измерения равна:
-ый интервал отдельного значения результата измерения равна: 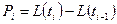 . Принимая во внимание, что
. Принимая во внимание, что 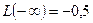 ,
, 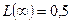 , поместим рассчитанные значения
, поместим рассчитанные значения 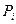 в следующую графу.
в следующую графу.
В 7 и 8 графы внесены вспомогательные величины. Суммирование чисел в последней графе даст 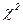 равное 2,528. Из графика
равное 2,528. Из графика 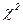 видно, что рассчитанное значение
видно, что рассчитанное значение 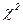 <<
<< 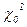 , соответствующего Р=0,95.
, соответствующего Р=0,95.
Т.о. можно применять гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятностей.
При проверке нормальности закона распределения по критерию Пирсона хорошие результаты получаются только при 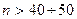 , при
, при 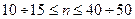 применяется составной критерий.
применяется составной критерий.
Сначала рассчитывается d, равное 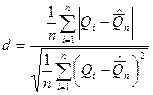 и проверяется выполнение условия
и проверяется выполнение условия 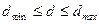 , где
, где 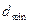 и
и 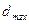 берется из таблицы для соответствующего значения доверительной вероятности.
берется из таблицы для соответствующего значения доверительной вероятности.
Если это условие соблюдается, то дополнительно проверяются хвосты законов распределения вероятности.
При  считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5
считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5 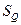 (стандартного отклонения);
(стандартного отклонения);
При - 2 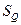 .
.
Несоблюдение хотя бы одного из 2-х условий достаточно для того, чтобы гипотеза о нормальности закона распределения была отвергнута.
При 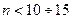 гипотеза о нормальности закона не проверяется.
гипотеза о нормальности закона не проверяется.
Решение принимается на основе априорной информации.
| <== предыдущая страница | | | следующая страница ==> |
| Точные оценки числовых характеристик | | | Обработка экспериментальных данных подчиняющихся нормальному закону распределения |
Дата добавления: 2014-08-04; просмотров: 322; Нарушение авторских прав

Мы поможем в написании ваших работ!