
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Кодирование квантованных сигналов
Квантованный сигнал, в принципе, можно считать кодовым с основанием кода равным числу М разрешенных уровней (уровней квантования) и с числом символов в кодовой группе, равным единице. Таким образом, квантованный сигнал является многоуровневым.
Многоуровневые сигналы весьма неудобны для передачи, так как приемник должен различать все разрешенные уровни. Кроме того, такие сигналы трудно восстановить (регенерировать), если они подверглись действию помех. Иными словами, многоуровневым сигналам в большей степени свойственны недостатки аналоговых сигналов. Поэтому в цифровых системах передачи обычно используются коды со сравнительно низким основанием , чаще всего двоичные. Процесс преобразования многоуровневого сигнала в код с низким основанием называется кодированием. Результатом кодирования является комбинация символов (посылок, цифр), представляющая в соответствующей системы счисления номер разрешенного уровня квантованного сигнала. В цифровых системах передачи широкое применение нашла двоичная система счисления. Запись любого квантованного уровня с М разрешенными уровнями в двоичной системе счисления может быть представлена в виде
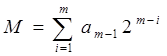 , ( 66 )
, ( 66 )
здесь m - число разрядов кода; аi - разрядная цифра, принимающая значения 0 или 1. С помощью m-разрядного двоичного кода можно закодировать число уровней квантования равного
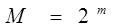 . ( 67 )
. ( 67 )
Поскольку выбор числа уровней квантования определяется допустимой величиной шага квантования, обычно приходится решать обратную задачу: определение минимально необходимого числа разрядов кода, который может быть использован для кодирования при заданном М. Из (67) очевидно, что для двоичного кода имеем
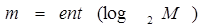 , ( 68 )
, ( 68 )
здесь ent (х) - означает, что берется целая часть числа х.
Например, для кодирования числа 111 необходимое число разрядов будет равно m=ent ( log2 M ) = ent ( log2111) = ent (6,79) =7 , а запись числа 111 в соответствии с (66) будет иметь вид
111= 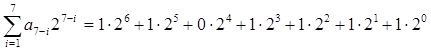 ,
,
т.е. ему соответствует кодовая комбинация 1101111, что соответствует значениям разрядных цифр равных а6 = 1, а5=1, а4=0, а3 =а2 =а1=а0= 1. Набор величин Qm-1 = 2m-i можно рассматривать как ряд эталонных сигналов, имеющих вес, определенный номером разряда. Для нашего примера Q6 = 64, Q5=32, Q4=16, Q3 = 8, Q2 = 4, Q1 = 2, Q0 = 1.
Однозначная связь величины эталонного сигнала с номером разряда двоичного эквивалента разрешенного квантованного уровня позволяет ограничиться передачей в системе связи только ряда величин аi , составляющих кодовую комбинацию (или кодовую группу).
Множество используемых кодовых комбинаций, связанных единым законом построения называется кодом. Простейшим кодом является код, в основе построения комбинаций которого лежит отношение (66), называется натуральным двоичным кодом. Графически коды удобно изображать кодовыми таблицами или кодовыми растрами, характеризующих форму взаимной связи уровней квантования и соответствующих им кодовых комбинаций, представляя их по порядку уровней. На рис. 9а показан кодовый растр 5-разрядного натурального двоичного кода, с помощью которого можно образовать 32 двоичных числа - кодовые комбинации и, следовательно, передать 32 квантованных уровня; 1(«единицы» или «импульсы») и 0 («нули» или «пробелы») показаны здесь соответственно черными и белыми квадратиками. Нумерация уровней дана сверху вниз, внизу указан вес разрядов кода.
Перестановка порядка следования кодовых комбинаций на обратный дает простой обратный код. Например, уровень М=22 в натуральном коде представляется комбинацией вида 10110 (см.рис.9а), обратный код выразится комбинацией вида 01101. Замена всех импульсов в кодовой комбинации на пробелы (или “единиц” на “нули”) приводит к инверсному коду. Так например, для М=22 в натуральном коде кодовая комбинация в инверсном коде будет иметь вид 01001.
Другой тип кода, применяемый в цифровых системах передачи, является код Грея (он же рефлексный или зеркальный). Его отличительной особенностью является то, что любые две соседние кодовые группы (см. рис.9б) отличаются друг от друга лишь в одном разряде. Это свойство используется при построении кодов и позволяет уменьшить ошибки кодирования. К коду Грея применимы понятия обратный или инверсный. Еще один класс составляют симметричные коды. Для кодирования отсчетов, например, речевых - телефонных сигналов, которые принимают более или менее одинаковые абсолютные значения выше и
а) б) в)
24 23 22 21 20
| -15 | ||||||||||||||||||
| -14 | ||||||||||||||||||
| -13 | ||||||||||||||||||
| -12 | ||||||||||||||||||
| -11 | ||||||||||||||||||
| - 10 | ||||||||||||||||||
| +1 | ||||||||||||||||||
| +2 | ||||||||||||||||||
| +3 | ||||||||||||||||||
| +4 | ||||||||||||||||||
| +5 | ||||||||||||||||||
| +6 | ||||||||||||||||||
| +7 | ||||||||||||||||||
| +8 | ||||||||||||||||||
| +9 | ||||||||||||||||||
| +10 | ||||||||||||||||||
| +11 | ||||||||||||||||||
| +12 | ||||||||||||||||||
| +13 | ||||||||||||||||||
| +14 | ||||||||||||||||||
| +15 |
Рис.9. Кодовые таблицы двоичных кодов:
а) натуральный двоичный код; б) рефлексный двоичный код Грея;
в) симметричный двоичный код
ниже своего нулевого уровня, может оказаться удобным использовать первый разряд для обозначения знака полярности, т.е. положительного или отрицательного, а остальные разряды обозначения абсолютной величины.
Если не принимать во внимание первый (высший ) разряд, определяющий полярность квантованного АИМ сигнала, то получающаяся кодовая таблица (кодовый растр) оказывается симметричной относительно своей середины. Ясно, рис.9б, что код Грея обладает свойством симметрии.
Перечисленными кодами техника цифровых систем передачи не ограничивается. Предложено большое количество кодов, целесообразность использования которых решается конкретными задачами кодирования и требованиями к достоверности передаваемой цифровой информации.
Кодовые группы после передачи по линейному тракту декодируются на приеме и по отсчетным значениям восстанавливается исходный сигнал.
В современных ЦСП процессы квантования и кодирования, как правило, совмещены и процесс формирования цифрового сигнала называется аналого-цифровым преобразованием (АЦП), а обратный процесс называется цифро-аналоговым преобразованием (ЦАП). Кодеры и декодеры, предназначенные для АЦП и ЦАП, в совокупности называются кодеками.
Обобщенная структурная схема цифровой системы передачи
В цифровых системах передачи с временным разделением каналов (ВРК) самое широкое применение нашла импульсно-кодовая модуляция (ИКМ). При формировании цифрового сигнала на основе ИКМ-ВРК осуществляются дискретизация и квантование аналоговых первичных сигналов, а затем их кодирование. Структурная схема оконечного оборудования цифровой системы передачи с временным разделением каналов на основе импульсно кодовой модуляции (ЦСП-ИКМ) приведена на рис.10, а временные диаграммы ее работы на рис.11. От других
 Тракт передачи каналов
Тракт передачи каналов
От других
каналов
Линия
К другим
каналам
| <== предыдущая страница | | | следующая страница ==> |
| Отсюда ОСШК на выходе ФНЧ демодулятора равно | | | Тракт приема К другим каналам |
Дата добавления: 2014-08-04; просмотров: 611; Нарушение авторских прав

Мы поможем в написании ваших работ!