Основные уравнения газового потока

Если движение газа через канал установившееся, то через каждое сечение канала в единицу времени протекает одно и то же количество газа.

Для этого случая (рис. 12.1) при определенной скорости газа в каждом сечении канала расход газа будет равен

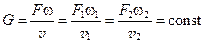(12.1)

где G — секундный массовый расход газа;

F₁, F₂, F₃ — площади поперечных сечений канала;

w₁,w₂,w₃— расходные скорости в соответствующих поперечных сечениях;

v₁, v₂, v₃ — удельные объемы в отдельных поперечных сечениях.

Постоянство массового расхода для всех сечений канала в каждый момент времени устанавливает условие неразрывности струи, поэтому уравнение (12.1) называют уравнением неразрывности или сплошности.

Для рассматриваемого процесса течения газа через канал уравнение первого закона термодинамики для G кг газа имеет вид

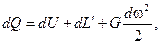(12.2)

где 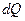— элементарное количество тепла, подводимое или отводимое от газа на рассматриваемом участке движения;

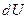— изменение внутренней энергии газа в соответствующих сечениях;

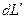— элементарная работа газа против внешних сил;

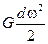— приращение кинетической энергии газа при eго перемещении на выделенном участке.

Рис. 12. 1

Работа газа против внешних сил в движущемся газе является работой, затраченной на его проталкивание.

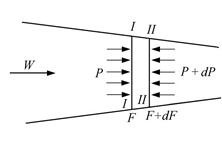
Рассмотрим поток газа в канале
(рис. 12.1) при одномерном течении. Выделим сечениями I-I и II-II некоторую массу газа. Притекающий к сечению I-I поток выполняет функцию поршня, который вытесняет заполняющий канал газ. На выделенную массу газа в канале будет действовать слева сила pF, а справа — сила (р+dp) (F + dF).

Работа перемещения, учитывая принятые в термодинамике знаки работ, будет равна

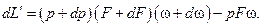(12-3)

После сокращения и отбрасывания малых величин второго и высшего порядка получим

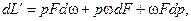(12.4)

или

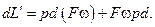(12.5)

Так как по уравнению неразрывности Fw = Gv и, учитывая то, что расход G есть величина постоянная, в сплошной среде

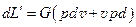(12.6)

(12.7)

Относя работу против внешних сил к 1 кг газа, получим

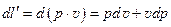(12.8)

Величина 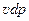определяет работу, произведенную элементарным объемом газа при условии, что выделенная масса газа несжимаема.

Второе слагаемое 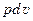представляет собой работу, которую перемещающийся объем газа должен совершить в результате деформации под действием равномерно распределенного давления.

Подставляя работу против внешних сил в уравнение первого закона термодинамики, записанное для 1 кг газа, будем иметь

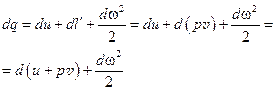(12.9)

Как известно из уравнения (3.10),

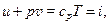(12.10)

следовательно

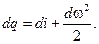(12.11)

Это уравнение показывает, что теплота, сообщаемая движущемуся газу, расходуется в двух направлениях: на приращение энтальпии газа и на приращение внешней кинетической энергии, т. е. идет на увеличение скорости газового потока.

Уравнение (12.11) является основным для потока газа или пара, причем оно справедливо как для обратимых, не сопровождающихся действием сил трения, так и для необратимых течений, сопровождающихся трением.

Для течений при наличии сил трения уравнение (12.11) должно быть дополнено 2-мя членами: один, учитывающий работу, расходуемую на преодоление сил трения, другой, выражающий приращение тепла в газовом потоке. Так как работа против сил трения полностью переходит в тепло, то эти два члена одинаковы по величине, имеют различный знак и поэтому взаимно уничтожаются. Наличие сил трения не может нарушить общего баланса Энергии, а лишь приводит к преобразованию одного вида энергии в другой.

При адиабатном течении газа, когда при движении газа через канал тепло ему не сообщается (dq = 0), будем иметь

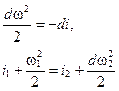(12.12)

Из уравнения (12.12) следует, что при теплоизолированном стационарном течении газа через канал сумма удельной энтальпии и удельной кинетической энергии сохраняет постоянное значение.

Уравнение (12.12) так же, как и (12.11), сохраняет силу как для обратимых, так и для необратимых течений. Следует отметить, что эти уравнения справедливы лишь в том случае, когда газ или жидкость при своем движении совершает работу расширения и не производит полезной (технической) работы (например, вращение рабочего колеса какой-либо машины, приводимой в движение потоком газа).

Для обратимого процесса истечения газа одновременно с уравнением (12.11) сохраняет силу и уравнение (4.7):

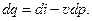
Подставив последнее уравнение в формулу (12.11), получим

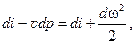
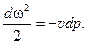
Приращение внешней кинетической энергии тела является как бы располагаемой работой, которая может быть использована в машинах и превращена в другие виды энергии.

Обозначим располагаемую работу через l₀, тогда

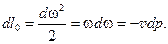(12.13)

Равенство (12.12) устанавливает основные особенности истечения газов. Из этого равенства видно, что w и dp имеют обратные знаки, т. е. при обратимом процессе увеличение скорости всегда связано с понижением давления, и наоборот, уменьшение скорости сопровождается повышением давления.

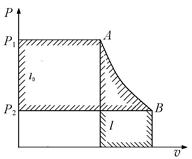
Рис. 12.2

Каналы. в которых происходит расширение газа с уменьшением давления (dp< 0) и увеличение скорости (dw >0), называются соплами.

Каналы, в которых происходит сжатие га­за с увеличением давления (dp > Q) и уменьшением скорости (dw < 0), носят название диффузоров.

Как видно из уравнения (12.13), необходимым условием получения располагаемой работы является падение давления, так как только при dp<0, dl₀ > 0. Если в течение процесса давление будет оставаться постоянным с/р = 0, то располагаемая работа будет равна нулю. Если процесс изменения состояния газа при его течении изобразить линией в координатах р—v (рис. 12.2), то для процесса истечения А — В располагаемая работа

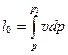
изобразится в виде площади, ограниченной кривой процесса, изобарами р = р₁ и p = p₂ и осью ординат. Работа расширения газа

будет по-прежнему изображаться площадью под кривой процесса, которая ограничена крайними ординатами и осью абсцисс.

В зависимости от вида процесса значение располагаемой работы может быть подсчитано на основе общих термодинамических положений. Располагаемая работа в политропном процессе, в котором изменение состояния подчиняется уравнению (pvⁿ = const), после подстановки в уравнение (12.13) значения текущего объема

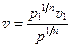
будет равна

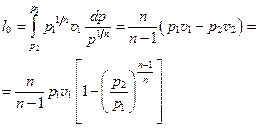(12.14)

В общем случае располагаемая работа может быть больше или меньше работы расширения или равна ей, причем это соотношение будет определяться величиной показателя политропы. Так, для политропного процесса, в котором работа расширения газа определяется по формуле

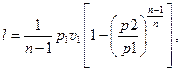
сравнение с располагаемой работой приводит к равенству

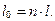
Для адиабатного процесса расширения газа

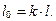
Для адиабатного течения газа располагаемая работа может быть определена и через энтальпию газа. Используя уравнение (12.12), видим, что

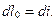
Интегрируя это выражение, получим

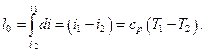(12.15)

Следовательно, располагаемая работа газа при адиабатном течении будет равна разности энтальпий в начальном и конечном состояниях. Эта разность энтальпий обозначается через h₀ и носит название располагаемого теплоперепада.

На рис. 12.3 и 12.4 показаны располагаемый теплоперепад и располагаемая работа в диаграмме i — s.

Дата добавления: 2014-08-04; просмотров: 461; Нарушение авторских прав

Мы поможем в написании ваших работ!