Представление переменных в виде изображений

Решение многих задач упрощается, если использовать символический метод расчёта.

Хевисайд (1850-1925)в качестве символа предложил оператор дифференцирования 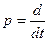, его размерность 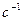. Заметьте, что такую же размерность имеет и угловая частота .

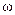Фурье (1768-1830) предложил периодическую функцию, изменяющуюся во времени, раскладывать вряд (ряд Фурье). Для периодических функций, изменяющихся с определённой угловой частотой 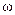, он ввёл понятие изображения:

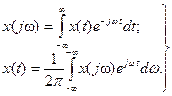(1)

Здесь, в первом уравнении с помощью оператора 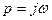выполняется переход от оригинала 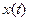к изображению 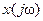, а во втором уравнении выполняется обратный переход. Оператор 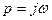зависит от частоты и имеет размерность 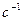. Это уже не оператор дифференцирования.

Лаплас (1749-1827) предложил рассматривать поведение переменных САУ в частотной области. Предполагается, что на вход системы подаётся гармонический сигнал. Он ввёл своё понятие частотного изображения:

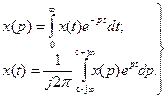(2)

Здесь 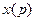- изображение рассматриваемой переменной 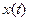, 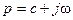- оператор, представляющий собой комплексное число. Вещественная часть с- абсцисса абсолютной сходимости, 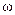- угловая частота в рассматриваемой области. Размерность 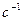, то есть такая же, как и у оператора дифференцирования (Хевисайда) и у оператора Фурье. Преобразования (2) справедливы только при нулевых начальных условиях, то есть 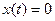при t < 0.

В отличие от преобразования Фурье (1) здесь изображение функции времени является функцией не частоты, а комплексного оператора р. Но оказывается, что, для большинства функций из области ТАУ действительная часть оператора р равна нулю, то есть с=0. Поэтому принимают 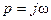. В этом случае преобразования Фурье и Лапласа формально совпадают, а сущность явлений разная. Решаемые задачи тоже разные.

В задачах электротехники при расчетах переходных процессов используют преобразование Карсона – Хевисайда, которое отличается от преобразования Лапласа (2) дополнительным умножением на величину р:

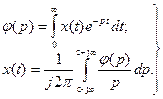(3)

Таким образом, между преобразованиями Лапласа и Карсона – Хевисайда существует соотношение

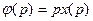. (4)

Основное достоинство преобразований Фурье, Лапласа и Карсона – Хевисайда заключается в том, что операции дифференцирования и интегрирования оригинала заменяются алгебраическими действиями по отношению к изображениям.

Преобразования Лапласа очень удобны при анализе и синтезе САУ. Математическое описание становится компактным, его обычно представляют в виде структурных схем. Эти схемы можно преобразовывать к нужному виду и с их помощью удаётся получать процессы с желаемым качеством.

Преобразования Карсона – Хевисайда удобны при расчёте переходных процессов.

Дата добавления: 2014-08-04; просмотров: 216; Нарушение авторских прав

Мы поможем в написании ваших работ!