
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МЕТОДЫ МОДЕЛИРОВАНИЯ
1.1 Предмет моделирования
Методы математического моделирования применяются на реальных статистических данных, получаемых с физически существующего объекта, изучением, исследованием или управлением которого занимается исследователь. Дадим некоторые определения.
Под объектом моделирования (ОМ) понимают часть физического или искусственного мира, ограниченного в пространстве и во времени. Объектами моделирования могут быть: электродвигатель, двигатель внутреннего сгорания, цех, предприятие, технологический процесс и т.д. Здесь важно иметь причинно-следственную зависимость между характеристиками объекта моделирования, которую можно представить в виде математического выражения (воздействие – отклик).
Под моделью понимают любое символьное отображение (описание) объекта моделирования. Математической моделью будем считать описание реального физического объекта математическими средствами.
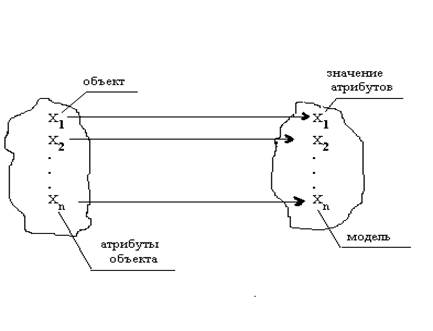
Рис. 1.1 Отображение физического объекта моделью
Выделенный исследователем объект может называться объектом управления, объектом моделирования, объектоминформатизации.Любой объект моделирования обладает набором характеристик или свойств. Эти свойства называются атрибутами, в свою очередь они могут быть представлены количественными, качественными (символьными), булевыми или другими типами переменных. Выбор атрибутов можно представить следующими этапами.
1 этап. Перечисляются все доступные описанию или измерению характеристики ОМ, обычно числовые. Например, для электродвигателя ими будут величина электрического тока, частота оборотов, момент на валу, мощность, вес, габариты и т.д.
2 этап. Выбираются атрибуты, значения которых представлены качественными значениями (цветовая гамма: красный, синий, зеленый и т.д.), т.е. значениями в символьной форме. Среди них могут быть и такие атрибуты, которые имеют числовую форму (каждому цвету соответствует числовое значение частоты). При моделировании значения символьных переменных также, как и значения числовых переменных, должны быть упорядочены, то есть ранжированы по некоторому правилу, например по возрастанию значений.
3 этап. Выбираются атрибуты, шкалы которых основаны на рефлексивном виде шкалы. Обычно эти шкалы вводятся для неизмеряемых и невычисляемых абстрактных атрибутов. Например, необходимо оценить «эффективность функционирования» некоторой системы, оценить «целесообразность» выбранной структуры объекта, определить «эволюционную способность» системы и т.д. На основе теории шкалирования составляется описание значений приведенных выше атрибутов объекта и способов отображения этих значений в виде некоторого ряда или таблицы. Этот тип переменных наиболее труден при описании и моделировании объектов.
Моделирование объектов можно представить тремя направлениями.
Концептуальное моделирование, в основе которого лежит представление объекта в виде таблиц, называемых объектными и связными отношениями (о.о., с.о.). Концептуальное моделирование наиболее распространено при проектировании баз данных автоматизированных систем управления. Результаты концептуального моделирования широко используются в математическом моделировании.
Физическое моделирование – в основе которого лежит представление объекта в виде физического объекта в той же или другой физической среде. Пример: исследование морских течений можно моделировать в бассейне, колебательные процессы можно моделировать в механической среде с помощью маятника либо в электрической среде с помощью LC- контура.
Математическое моделирование - в основе которого лежит представление объекта в виде анализа и исследования реального мира математических и аналитических зависимостей.
Аналитическая зависимость может быть представлена четырьмя видами:
- функциональная форма
y = f (x);
- графическая форма
Рис. 1.2. График функции
- табличная форма
| Y | X |
| Y1 | x1 |
| yn | xn |
- описательная форма(описание функции на одном из языков).
Наиболее важной характеристикой качества моделирования является соответствие моделей реальным объектам. Это соответствие определяется мерой идентичности (адекватности) и оценивается методами математической статистики. Наиболее распространенными методами, определяющими эту меру, являются:
-метод наименьших квадратов;
-метод максимума правдоподобия;
-статистические методы (Пирсона, Стьюдента, Хотеллинга, Бартлетта, Колмогорова-Смирнова и т. д.);
- комбинированные методы.
Математическое моделирование содержит две феноменологически самостоятельные составляющие, которые можно представить в виде последовательных этапов моделирования.
Первый этап построения моделей сводится к определению вида модели и подбору параметров модели (коэффициентов), о которой ничего не известно. Например, задают вид модели, зная физическую природу объекта или явления, а затем на основе экспериментов определяют значения коэффициентов модели. Но если априорные сведения очень малы или не точны для моделирования, то используют методы структурной идентификации, при которой на основе статистического материала постулируются аналитические зависимости для этого объекта. Модели определяются на основе некоторого класса аппроксимирующих функций, для которых оценивается мера идентичности. При построении модели используют методы определения существенных переменных, методы выбора структуры модели, методы оценивания параметров (коэффициентов при функциях).
Второй этап сводится к исследованию полученной модели. Производятся расчеты поведения объекта при различных значениях его атрибутов. Для сложных объектов используются модели имитационного моделирования, при котором модель объекта подвергается случайным возмущениям и исследуются реакции объекта на эти возмущения.
| <== предыдущая страница | | | следующая страница ==> |
| УДК 681.5.015:519.237 | | | Методы построения моделей |
Дата добавления: 2014-08-04; просмотров: 422; Нарушение авторских прав

Мы поможем в написании ваших работ!