ИНТЕРПОЛЯЦИЯ

2.1 Задача интерполяции

Интерполяция функции Х(t) одной переменной t, заданной (n+1) узлами (дискретами) Х_i(t_i), где i=0,1,2,…,N, N ¾ число дискрет, n ¾ порядок полинома, заключается в нахождении значения Х по значениям t, находящимся в промежутках между узлами t_i. При интерполяции функция Х_i(t_i) заменяется интерполяционным полиномом L(t), значения которого в узлах точно совпадают с Х(t_i). Значение N задает степень полинома L(t). n=N-1.

Пусть задана функция в виде дискрет Х_i(t_i)

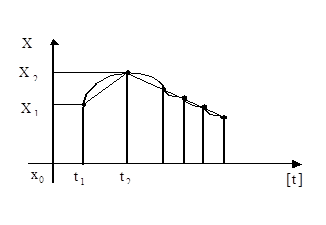
Рис. 2.1. График интерполяции функции:

[ t ] - дискретное время (непрерывное ( t ))

Пусть дан набор значений в виде пар значений аргумента и функции

(t₀, x₀), (t₁, x₁),…….(t_N, x_N).

Необходимо определить x ® f ( t ) (где t- непрерывно).

Определение значений функций внутри интервала (отрезка) по ее значениям на концах этого отрезка является задачей интерполяции. Определение значений функции за пределами отрезка является задачей экстраполяции.

Исходные дискреты для интерполяции математически записываются:

X_i =L(t_i), i = 0,1,…..N.

Графический вид интерполяционного полинома определяется его порядком (степенью для ряда Тейлора):

n=N-1.

Например, интерполяционный график синусоиды при линейной интерполяции и соответствующем наборе точек (дискрет) имеет вид

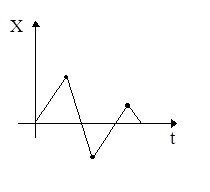
Рис. 2.2 Линейная интерполяция синусоиды

Наиболее часто применяют сплайн интерполяцию (требует вычисления производных). Это гладкая интерполяция, обеспечивающая нужную погрешность. Слово spline переводится как «гибкая линейка». При интерполяции эта линейка точно проходит через узлы, осуществляя плавный переход через узел от одного интервала интерполяции к следующему. Такой переход аналитически реализуется за счет вычисления производных и учета их при построении функций сплайн-интерполяции.

При меньшем шаге дискретизации и достаточно большом набором дискрет, а следовательно, и большей степени (обычно выбирают не менее 9 дискрет, для синусоиды при этом порядок интерполяционного полинома равен n=9–1=8) интерполяционного полинома получим более гладкую синусоиду.

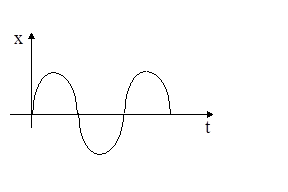
Рис 2.3. Интерполяция синусоиды полиномами восьмой степени

Дата добавления: 2014-08-04; просмотров: 374; Нарушение авторских прав

Мы поможем в написании ваших работ!