ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ РЕЗОНАНСНОГО ПОГЛОЩЕНИЯ (ЭФФЕКТ ДОПЛЕРА)

Формула Брейта-Вигнера правильно описывает сечение резонансного взаимодействия нейтрона в системе координат, связанной с центром масс системы нейтрон-ядро мишени (при 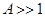центр масс практически совпадает с положением ядра). Ядра среды совершают тепловое движение и, поэтому, в каждом акте столкновения нейтрона с ядром, должна вводиться своя система отсчета, движущаяся вместе с ядром, в то время как энергия нейтрона 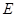в наших расчетах рассматривается в единой лабораторной системе. В принципе энергия замедляющегося нейтрона существенно выше энергии теплового движения ядер. Поэтому при изучении процесса замедления нейтронов пренебрегают энергией движения ядер и рассматривают процесс столкновения нейтронов с неподвижными ядрами среды. Однако, в случае резонансного взаимодействия нейтронов с ядром естественная ширина резонанса 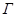сравнима со средней энергией теплового движения ядер 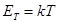, где 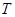– температура среды по шкале Кельвина.

Для понимания сути явления, рассмотрим одномерную и односкоростную модель движения ядер среды, а именно, будем считать, что все ядра среды имеют одну и туже скорость движения, причем половина из них движется по направлению движения нейтрона, а другая половина движется в противоположном направлении.

РИСУНОК

Полное число взаимодействий нейтронов с ядрами резонансного поглотителя в лабораторной системе отсчета, равное 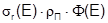, можно представить в виде суммы, слагаемые которой представляют собой число взаимодействий нейтронов с ядрами резонансного поглотителя, движущимися по определенному направлению относительно скорости нейтрона. Для выбранной модели эта сумма включает всего два слагаемых

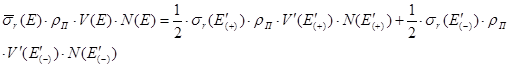
где 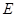– энергия нейтрона в лабораторной системе координат,

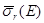– резонансное сечение, выраженное относительно энергии нейтрона в лабораторной системе координат,

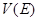– скорость нейтрона в лабораторной системе координат,

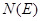– плотность нейтронов с энергией Е,

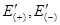- энергия относительного движения нейтрона в системе центра масс для ядер, движущихся по и против направления движения нейтрона соответственно,

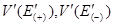- скорость относительного движения нейтрона в системе центра масс для ядер, движущихся по и против направления движения нейтрона соответственно. Так как плотность нейтронов не зависит от того, в какой системе отсчета рассматривается энергия нейтрона, то

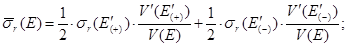
В системе центра масс скорость нейтрона и его энергия выражаются через скорость движения ядер следующим образом

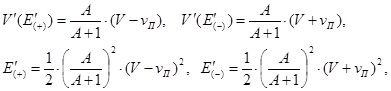
Поскольку для ядер резонансного поглотителя 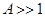, то 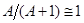. Кроме того, скорость теплового движения ядер 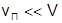, поэтому

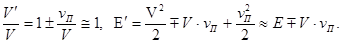
Учитывая эти соотношения, получим

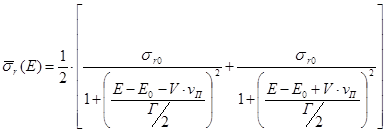
Так, например, при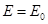

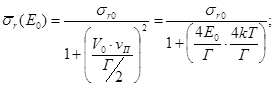
По предположению средняя энергия теплового движения ядер 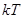сравнима с естественной шириной резонанса, т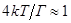о , но 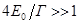и поэтому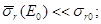

ДАТЬ РИСУНКИ ДВУХ РЕЗОНАНСНЫХ КРИВЫХ В СИСТЕМЕ ЦЕТРА МАСС И ЛАБОРАТОРНОЙ СИСТЕМЕ

Анализируя это выражение, можно показать, что

1.

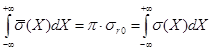
то есть площадь под резонансной кривой, как в системе центра масс, так и в лабораторной системе координат, не изменяется. Это значит, что не изменяется и величина резонансного интеграла I_R. Отсюда следует, что доплеровский эффект не оказывает влияния на поглощение нейтронов слабыми резонансами и оно не зависит от температуры среды.

2.

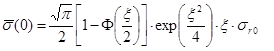
где 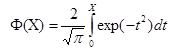- интеграл вероятности. При x<<1 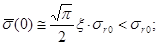а при x>>1 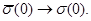. С ростом температуры величина x падает, а с ней уменьшается и резонансное сечение в центре резонансной линии. Поскольку площадь под резонансной линией сохраняется, это означает, что происходит уширение резонанса. Для ²³⁸U сечение в максимуме для резонансов, относящихся к большим энергиям, падает примерно в 5-10 раз. Таким образом, обычный резонансный интеграл как бы отвечает условию 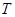=0, поскольку, 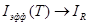при 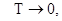но всегда имеет место следующее соотношение

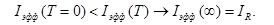(72)

В общем случае

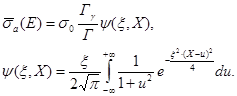(73)

Дата добавления: 2014-08-09; просмотров: 334; Нарушение авторских прав

Мы поможем в написании ваших работ!