
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Матричное объединение многослойных НС
Эта архитектура реализуется, если несколько линейных процессоров объединить в системы более высокого порядка. Схема будет выглядеть следующим образом:
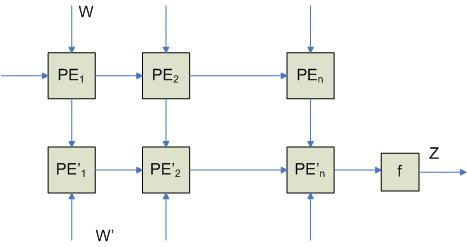
В результате такой схемы отдельных линеек отдельных системных процессоров получается систолический массив, с помощью которого можно решать задачи. При этом атомарные элементы образуются на основе линейных массивов.
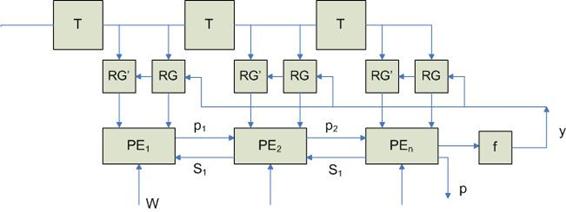
Реализация релаксационных НС на основе систолических массивов
К этим типам сетей относятся сети Хопфилда, Хэмминга и т.д.
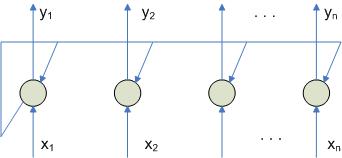
Для таких сетей необходимо соблюдение следующих условий:
1. 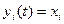
2. 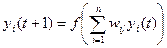
3. для всех нейронов 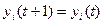
Следовательно, для окончания процедуры необходимо в систолическом массиве зафиксировать состояние равновесия.
p – сигнал, определяющий состояние равновесия.
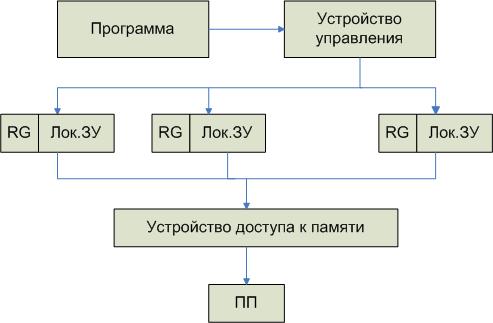
Первые n тактов работы сети Хопфилда в регистры RG заносятся компоненты неизвестного образа, которые поступают извне. Затем – поступают данные с выхода. Основная задача – определить момент равновесия. Если p=1, то процедура обучения продолжается.
Реализация процессорного элемента PE:
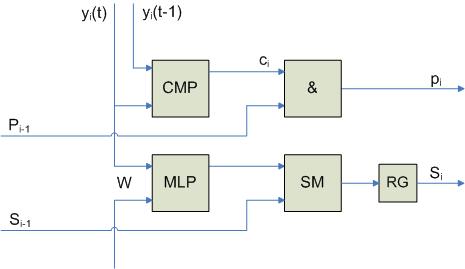
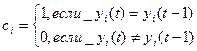
RG хранит текущее значение 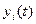 , а RG’ – текущее значение
, а RG’ – текущее значение 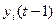 . В схеме сравнения используется суммирование по модулю 2. Общий сигнал p формируется как функция от всех выходов pi:
. В схеме сравнения используется суммирование по модулю 2. Общий сигнал p формируется как функция от всех выходов pi:
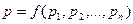
Когда значение p какой-то схемы становится равным 1, то возникает прерывание и из регистра RG выделяется соответствующий компонент образа.
Теоретическое исследование параллельных структур вычислительных систем
Чисто пользовательская архитектура – RAM (Random Access Machine). Машина параллельного типа – PRAM.
Основные характеристики RAM:
1. последовательный доступ к памяти;
2. последовательная работа всех устройств (чтение, вычисление, запись);
3. время выполнения алгоритма зависит:
- от объема;
- от выполняемых действий;
- от необходимости сохранения результата.
Основные характеристики PRAM:
1. независимость от способа организации связей между процессорами, что обеспечивает концентрацию параллелизма в задаче;
2. архитектура состоит из процессорных элементов, связанных с глобальной памятью. Поэтому доступ в PRAM аналогичен доступу в однопроцессорной системе.
Особенности PRAM:
1. состоит из отдельных процессорных элементов, каждый из которых является RAM;
2. каждый процессор имеет одно и то же время доступа к любой ячейке памяти;
3. связь между процессорами осуществляется через «доску объявлений»;
4. время выполнения – один шаг алгоритма.
Способы реализации PRAM
PRAM – память с произвольным доступом, который не зависит от типа связи, что позволяет концентрироваться на алгоритмах решения задач.
Это теоретическая модель, в которой не учитываются нюансы реализации, предназначена для обработки параллельных алгоритмов.
Работа модели осуществляется в 3 этапа:
1. чтение, которое одновременно может выполняться всеми процессорами;
2. выполнение программы процессорами;
3. запись.
Вводятся различные типы команд:
1. ER (Exclusive Read) – выполнение чтения осуществляется только одним процессором;
2. CR (Concurrent Read) – выполнение чтения осуществляется одновременно всеми процессорами;
3. EW (Exclusive Write) – выполнение записи осуществляется только одним процессором;
4. CW (Concurrent Write) – выполнение записи осуществляется одновременно всеми процессорами;
Разрешение конфликтов
Разрешение конфликтов осуществляется при использовании различных вариантов записи и чтения. Схема разрешения конфликтов следующая:
1. CW с приоритетом – у каждого процессора свой приоритет;
2. общее CW – все процессоры должны записать свои значения в одну и ту же ячейку памяти;
3. произвольная запись одного из процессоров в заданную ячейку памяти. Если одновременно есть несколько процессоров, готовых к записи, то записывается значение одного из них.
4. объединяющая CW – если несколько процессоров хотят записать в ячейку памяти свой результат, то происходит объединение результатов.
4 наиболее распространенных модели для разрешения конфликтов записи/чтения:
1. CR EW – разрешается одновременное чтение, запрещена одновременная запись;
2. ER EW – более строгая модель, одновременная запись и чтение запрещены;
3. CR CW – одновременная запись и чтение разрешены;
4. ER CW.
Таким образом, PRAM – модель параллельного вычислителя, который позволяет добиться оптимальной организации вычислительного процесса при выполнении некоторых фундаментальных алгоритмов.
Выполнение алгоритма поиска минимума в массиве на параллельных системах
Более эффективная процедура – использование метода сдваивания. Время реализации алгоритма пропорционально размерности массива.
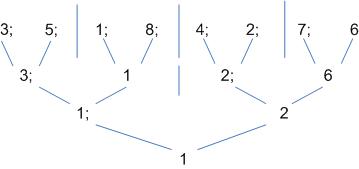
Таким образом – всего 3 шага.
Для реализации алгоритма необходимо обрабатываемые данные поместить в горизонтальный массив. Каждый элемент – в отдельном регистре.
Число процессоров избыточно. Для более эффективной реализации возможны варианты:
1. сократить число процессоров;
2. понизить время реализации;
3. сократить число процессоров и понизить время реализации.
Улучшенный алгоритм поиска минимума:
Пусть имеется P процессоров и D данных. Тогда для повышения эффективности каждому из процессоров поставим в соответствие D данных. На каждом этапе каждому процессору доступно D данных. Количество процессоров можно значительно понизить.
Повышение эффективности работы алгоритма осуществляется за счет двухэтапной процедуры обработки элементов.
Второй способ – поиск элемента в массиве. Весь массив разделяется на подмассивы, в которых каждый из процессоров ищет нужный элемент.
Ключевые понятия для организации вычислений в PRAM: разделяемая и распределенная память.
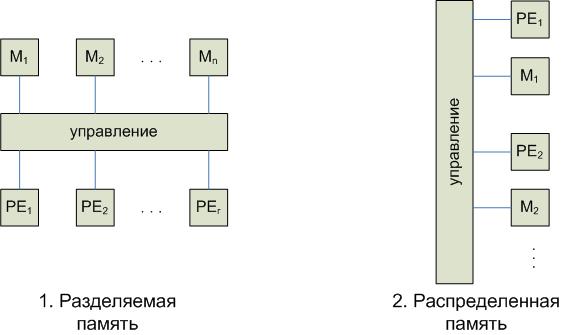
В первом случае каждый из процессоров имеет доступ ко всей памяти. Во втором случае процессор может обратиться к другому процессору только через механизм NUMA.
Основные критерии оценки сети процессоров, которые используются для реализации параллельных алгоритмов:
1. степень сети – это количество двунаправленных каналов связи, подключенных к процессору. Показывает, со сколькими процессорами связан текущий процессор, т.е. фактически это максимальное число;
2. диаметр сети – максимум из минимальных расстояний между всеми процессорами в сети;
3. пропускная способность – минимальное количество связей между процессорами, которое надо удалить, чтобы получить две равные по размеру подсети;
4. время выполнения операций в сети процессора (фундаментальные операции: префиксное вычисление, сортировка и т.д.).
Для снижения стоимости сети процессоров необходимо:
1. уменьшить время пересылки данных от одного процессора к другому;
2. для снижения количества конфликтов требуется максимальная пропускная способность;
3. минимальная степень сети.
Структуры сетей процессоров
Различные модели сетей процессоров характеризуются следующими параметрами:
1. схемы взаимодействия процессоров между собой;
2. память должна быть распределена;
3. особенность архитектуры сети;
4. диаметр сети;
и др.
Два процессора являются соседями, если они связаны между собой каналом связи.
Линейная сеть процессоров

Каждый элемент связан с двумя соседями. Степень сети равна 2 для внутренних элементов и 1 – для крайних.
Диаметр сети = n.
Пропускная способность = 1.
Пример:
Найти минимум в массиве: 3; 4; 2; 6; 15.
| шаг | p1 | p2 | p3 | p4 | p5 | min |
Повышение эффективности решения задач на линейной сети процессоров
1. Разбиение всей последовательности элементов на отдельные группы
Далее ищется минимум на множестве 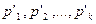 . Это делается либо стандартным способом (см.предыдущую главу), либо гусеничным алгоритмом (tractor thread). В этом алгоритме можно пересылать данные через линейную сеть процессоров в разных направлениях.
. Это делается либо стандартным способом (см.предыдущую главу), либо гусеничным алгоритмом (tractor thread). В этом алгоритме можно пересылать данные через линейную сеть процессоров в разных направлениях.
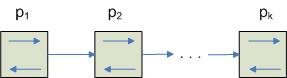
При использовании тракторного алгоритма одновременно можно решать несколько задач каждым из процессоров: нахождение минимального элемента, максимального элемента, заданного элемента. Все элементарные операции могут быть выполнены за один проход.
Задача сортировки:
В этом случае по окончанию ввода данных самый левый процессор должен хранить минимальный элемент. Одновременно происходит засылка данных и их сортировка.
 3, 4, 2. 6, 1, 5
3, 4, 2. 6, 1, 5
| Такт | p1 | p2 | p3 | p4 | p5 | p6 |
| | ||||||
| | ||||||
| |
Преимущество такого подхода:
количество шагов, необходимых для сортировки примерно равно числу элементов. Это оптимальный алгоритм сортировки для линейной сети процессоров. Данный алгоритм аналогичен алгоритму сортировки выбором.
2. Вычисление параллельного префикса
i-й префикс – это какая-либо ассоциативная бинарная операция, выполняемая на элементах первых i процессоров. Для решения такого типа задач сначала необходимо получить:
1. операцию на первых двух элементах 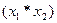 ;
;
2. 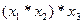 - операция с участием трех процессоров;
- операция с участием трех процессоров;
и т.д.
В конце выполнения операции параллельного префикса последний элемент содержит результат.
Следующий тип сети процессоров – кольцо.
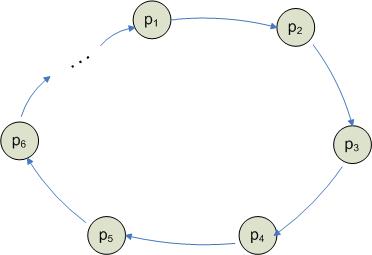
Степень кольца = 2.
Диаметр = 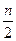 .
.
Матричные сети процессоров
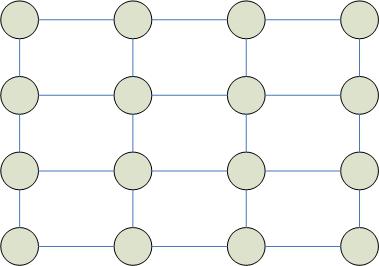
Наибольшая степень связности = 4.
На основе матричной сети процессоров можно строить различные конфигурации, которые будут наиболее эффективны для определенных типов решаемых задач.
Матричную сеть можно рассматривать как набор линейных сетей процессоров, установленных одна над другой и взаимосвязанных. Поэтому каждую строку и каждый столбец можно рассматривать как линейку процессоров. Поэтому все алгоритмы, предназначенные для решения различных типов задач, можно использовать для решения тех е задач на матричных процессорах.
Циклический сдвиг в матричной сети процессоров осуществляется одновременно в каждой строке и каждом столбце.
Матричные сети используются для решения тех задач, которые связаны с выполнением полугрупповых операций. Кроме того, в матричной системе очень легко решается задача копирования данных по процессорам путем сдвига. Задача сортировки так же легко выполнима.
Древовидная структура процессоров
Дерево формируется как бинарное с n процессорами на базовом уровне. Такое дерево имеет в общей сложности 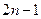 процессоров.
процессоров.
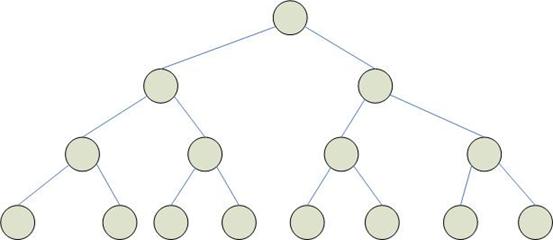
Максимальная связанность = 3.
Диаметр сети меньше, чем в других структурах. Выполнение операций в дереве (таких, как поиск минимума или максимума) требует гораздо меньше времени, чем при использовании других архитектур процессоров. Задача сортировки выполняется значительно хуже, т.к. идет пересылка от левых крайних элементов к крайним правым.
Недостаток: трудность решения задач, связанных с частым перемещением данных.
Преимущество: быстрое выполнение операция объединения данных, что свойственно задачам трансляции.
Целесообразно объединить древовидные структуры с матричными. Полученные в результате структуры – пирамидальные.
Пирамидальные структуры процессоров
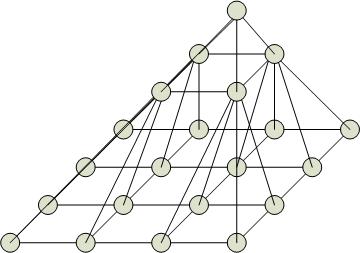
Основание пирамиды (уровень 0) – матрица процессоров. Уровень 1 – также матрица процессоров. Уровень 2 – вершина.
Пирамиду, в основании которой n процессоров, можно рассматривать как сеть процессоров, соединенных как четверичное дерево, в котором на каждом уровне находится матрица процессоров, соединенных с нижележащими процессорами.
Использование такой структуры позволяет решать сложные задачи, связанные с одновременным выполнением элементарных операций.
Если в основании n процессоров, то общее количество вершин = 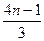 .
.
Каждый процессор основания связан с 4-мя своими соседями и со своим предком.
Максимальная степень = 9.
Диаметр сети = 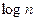 .
.
Древовидно-матричная структура процессоров
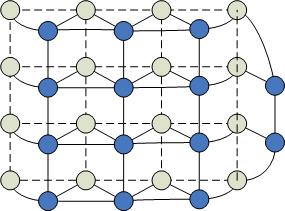
Максимальная степень = 6, при этом процессоры по краям матрицы имеют меньшее число связей.
Процессоры, находящиеся непосредственно в матрице называются процессорными листьями.
Диаметр сети: количество путей значительно больше, чем в других архитектурах, что приводит к созданию более эффективных алгоритмов. Передавать информацию можно одновременно в разных направлениях.
Пример:
Найти минимум в последовательности: 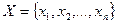
1. используется дерево строки над множеством данных, располагающихся в строке;
2. после получения результата в корне этот результат передается во все процессорные листья (т.е. в матрицу);
3. используя дерево над каждым столбцом, одновременно выполняются операции внутри каждого столбца;
4. корневые процессоры каждого из столбцов посылают результаты во все процессорные листья. Все процессоры получают конечный результат.
Сортировка части последовательности.
Пусть дан вектор 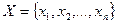 . Необходимо упорядочить эту последовательность и расположить ее в первом процессорном элементе.
. Необходимо упорядочить эту последовательность и расположить ее в первом процессорном элементе.
Будем использовать сортировку подсчетом. Для каждого элемента x подсчитывается число элементов, которые меньше x, что будет определять место числа в последовательности, т.е. вычисляется ранг x.
Для выполнения алгоритма требуется выполнить сравнение xi и xj.
Алгоритм:
1. засылаем в 1-ю процессорную линейку все элементы;
2. рассылаем элементы 1-й линейки во все остальные линейки;
3. в каждой строке i элемент xi, находящийся на главной диагонали матрицы, выставляется перед всеми элементами выставляемой строки. Создаются пары элементов для сравнения;
4. Вычисляем ранг элемента на главной диагонали.
| 5 9 4 2 | à | 5, 5 | 5, 9 | 5, 4 | 5, 2 | r = 2 |
| 5 9 4 2 | à | 9, 5 | 9, 9 | 9, 4 | 9, 2 | r = 3 |
| 5 9 4 2 | à | 4, 5 | 4, 9 | 4, 4 | 4, 2 | r = 1 |
| 5 9 4 2 | à | 2, 5 | 2, 9 | 2, 4 | 2, 2 | r = 0 |
Одновременно решаются 2 задачи:
1. поиск минимума;
2. упорядочение множества.
Основные преимущества:
1. высокая гибкость;
2. высокая скорость передачи данных;
3. простота организации.
Гиперкуб
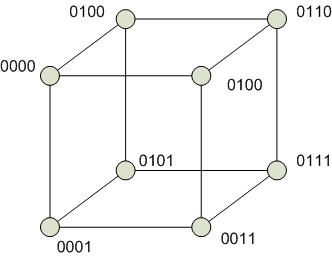
Степень строго не определена. В отличие от других архитектур связанность в гиперкубе можно наращивать. Степень одинакова для всех вершин. Отсутствие фиксированной архитектуры является и недостатком.
Диаметр гиперкуба пропорционален 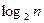 , где n – число вершин. При этом между любой парой вершин гиперкуба существует путь минимальной длины.
, где n – число вершин. При этом между любой парой вершин гиперкуба существует путь минимальной длины.
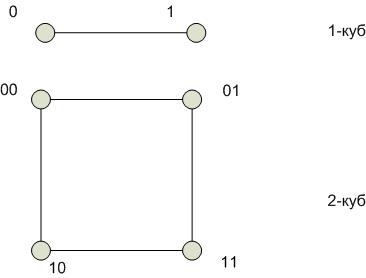
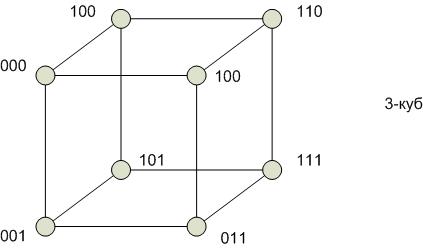
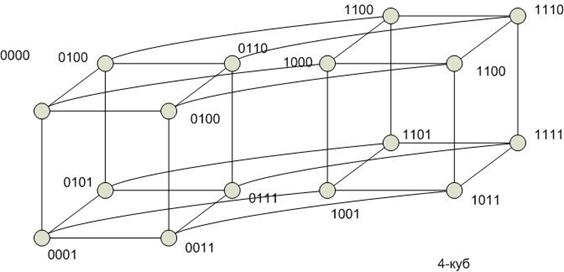
Выполнение операции поиска минимума на гиперкубе:
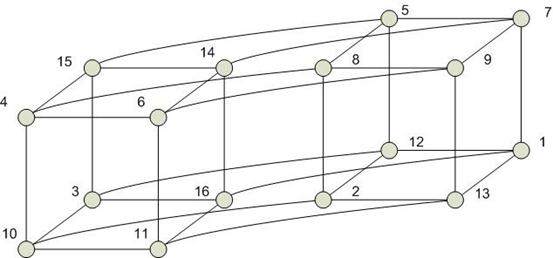
1. из правого куба пересылаются данные между одноименными вершинами, которые имеют разницу только в одном разряде:
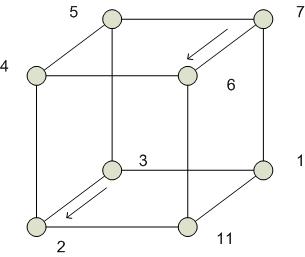
2.
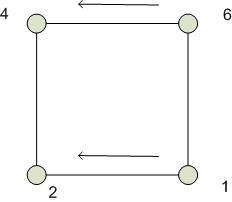
3.

4. 1
Особенностью гиперкуба является возможность моделирования на нем других сетевых архитектур. Тогда ребра куба моделируют каналы передачи информации.
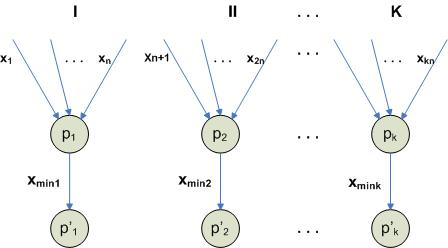
Систематика Флинна для выполнения параллельных алгоритмов
Для параллельных алгоритмов несколько изменяется классификация Флинна. Реализация SIMD (один поток, множество данных):
1. классический SIMD;
2. SPMD – на единственном процессоре, у которого есть возможность работы со многими данными.
Решение задач линейной алгебры на матричной сети процессоров
Наиболее эффективно решаются задачи, связанные с обработкой матриц. Пусть дана матрица размерности 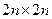 , требуется вычислить элемент
, требуется вычислить элемент 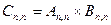 .
.
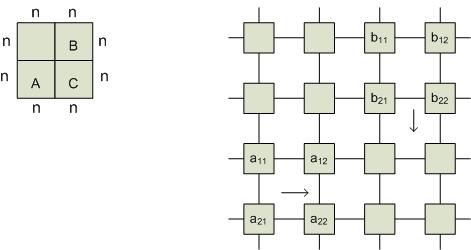
Суть алгоритма: элементы матриц А и В продвигаются своим соседям соответственно по строкам и столбцам: а – вправо, b – вниз – и поступают в процессоры нижней правой четверти.
Тогда получим:
1-й шаг. Все процессоры, содержащие элементы первой строки матрицы А, пересылают элементы вправо, а процессоры, содержащие элементы первого столбца В, посылают элементы вниз. В процессоре (*) образуется элемент С1,1.
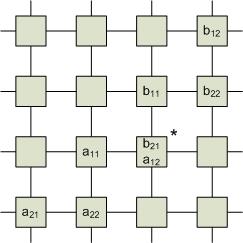
2-й шаг. Элементы первой строки А продолжают движение вправо, а элементы первого столбца В – вниз. За время, пропорциональное размерности матрицы, происходит вычисление всех элементов.
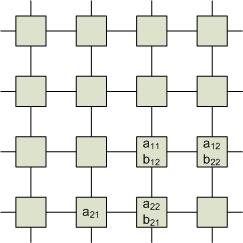
По производительности алгоритм в n раз более быстрый, чем обычные вычисления.
Реализация параллельных префиксов на различных архитектурах параллельных систем
Сложение последовательности чисел
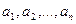
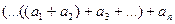
При рассмотрении теоретических моделей вычислителей изначально предполагается, что данные хранятся непрерывно, т.е. в соседних ячейках памяти или в смежных процессорах.
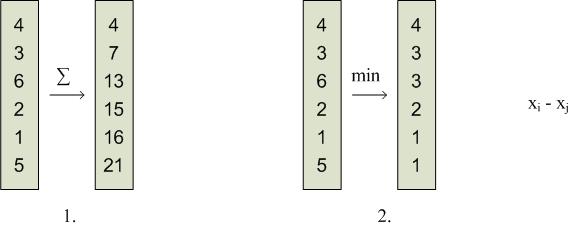
i, j – индексы элементов последовательности, над которыми выполняется операция. Объединение в сегменты упрощает выполнение и уменьшает его время.
Рассмотрим последовательность, состоящую из определенного числа элементов: 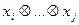 ,
, 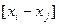 .
.
Например, последовательность S1,19.
1. x19
2. x18 – x19
3. x16 – x19
4. x12 – x19
5. x4 – x19
6. x1 – x19
Сложность алгоритма пропорциональна 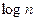 .
.
Пример 1:
| Исходные данные | |||||||||||
| Шаг1 | |||||||||||
| Шаг 2 | |||||||||||
| Шаг 3 | |||||||||||
| Шаг 4 |
Пример 2:
Операция объединения – непрерывное объединение смежных пар элементов.
| Исходные данные | ||||
При увеличении числа элементов сложность реализации таких алгоритмов растет. При этом можно увеличить либо время реализации, либо число процессоров, на которых выполняются операции.
| Исходные данные | ||||||||||||||||
| Шаг 1 | ||||||||||||||||
| Шаг 2 | ||||||||||||||||
| Шаг 3 |
На 3-ем шаге осуществляется объединение и обновление элементов.
Пример 3:
Объединение префиксов на матричной сети процессоров.
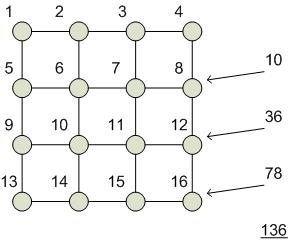
Шаг 1 – распределение данных по процессорам.
Шаг 2 – циклический сдвиг вправо во всех строках матрицы процессоров с одновременным вычислением суммы. Глобальные префиксы – в правом столбце.
Шаг 3 – циклический сдвиг в правом столбце.
Шаг 4 – циклический сдвиг влево построчно (для обновления данных).
Принцип реализации параллельных алгоритмов «разделяй и властвуй»
Этот принцип состоит из трех частей:
1. разделение задачи на подзадачи;
2. рекурсивное решение этих подзадач;
3. объединение решений подзадач в единое решение.
Этот принцип представляет собой построение рекурсивного дерева.
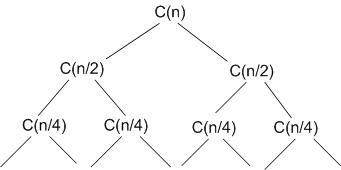
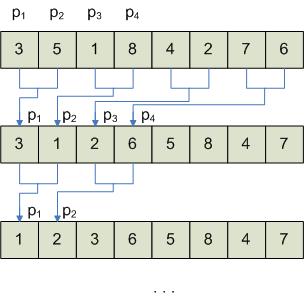
Сначала получаем решения на последнем уровне, затем объединяем их. Наиболее типовой задачей здесь является сортировка слиянием. Рассмотрим реализацию такой схемы в линейной сети процессоров.
Исходные данные: 3, 1, 8, 4, 5, 2, 7, 6.
1. делим данные на 2 последовательности: 3, 1, 8, 4 | 5, 2, 7, 6
2. проводим упорядочение каждой из подпоследовательности путем циклического сдвига либо на основе алгоритма подсчета ранга каждого из элементов. Каждый из в подпоследовательности получает индекс.
1, 3, 4, 8 | 2, 5, 6, 7
3. Объединение подпоследовательности в единую:
Каждый процессор Pi, 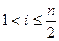 , «знает», что элемент, который он в данный момент содержит, является i-м элементом в подпоследовательности.
, «знает», что элемент, который он в данный момент содержит, является i-м элементом в подпоследовательности.
Для объединения двух подпоследовательностей в единую, надо знать ранги элементов в своей и другой части последовательности.
Основные недостатки:
1. требуется, чтобы во время каждого рекурсивного шага объединения циклический сдвиг мог выполняться только для одной подпоследовательности;
2. время выполнения алгоритма соизмеримо со временем реализации tractor thread (т.е. довольно велико).
Решение задачи выбора на линейной сети процессоров
К задачам выбора относятся следующие типы задач:
- нахождение минимального значения;
- нахождение максимального значения;
- нахождение медианы.
Пусть дан массив 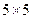 .
.
1. сортировка внутри каждого элемента массива.
2. выбор медианы.
S[3], S[8], S[13], S[18], S[23]
3. выбор медианы из всех медиан.
Сравниваем все элементы с медианой и делим на 3 группы: большие медианы, меньшие медианы, равные медиане.
Реализация на PRAM:
1. сортировка внутри каждого из элементов массива;
2. определение медиан, нахождение наименьшей:
3. распределение по зонам на основе алгоритма параллельного префикса.
На матричной сети процессоров используются в основном алгоритмы:
- сортировки;
- распределение элементов по онам.
Для матричной сети процессоров наиболее эффективной является быстрая сортировка.
Пример:
Исходный массив: 5, 8, 1, 2, 6, 7, 4, 9, 3.
Первый шаг – «разделяй»:
Small: 1, 2, 4, 3.
Med: 5.
Big: 8, 6, 7, 9.
Второй шаг – «властвуй» – упорядочивание внутри каждой зоны, после чего – объединение этих зон, получение окончательного результата:
1, 2, 3, 4. 5, 6, 7, 8, 9.
По сравнению со слиянием быстрая сортировка имеет преимущество: простое объединение, но более сложное разбиение.
Решение задачи быстрой сортировки на гиперкубе
Задача Quick Sort Hyper:
1. предполагается, что n элементов располагается по 2d вершин гиперкуба. Каждая вершина содержит 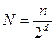 элементов;
элементов;
2. каждый процессор сортирует свои n элементов независимо;
3. 0-я вершина гиперкуба определяет медиану своих n элементов;
4. 0-я вершина может рассылать свою медиану всем 2d узлам.
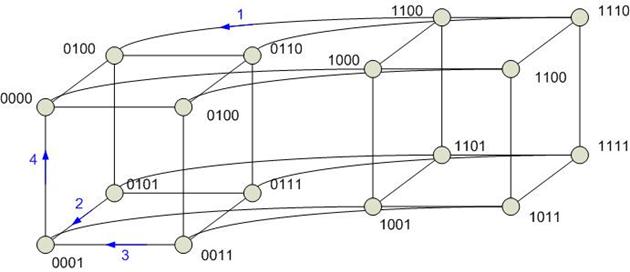
1-й шаг – ребро 1
2-й шаг – ребро 2
3-й шаг – ребро 3
4-й шаг – ребро 4.
| <== предыдущая страница | | | следующая страница ==> |
| ГЛОБАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ | | | Как следует из самого определения пожара – основной процесс, протекающий на пожаре, это горение |
Дата добавления: 2014-08-09; просмотров: 438; Нарушение авторских прав

Мы поможем в написании ваших работ!