Линейные электрические цепи при гармоническом воздействии

Постоянный ток не нашел широкого применения в промышленности, поскольку на практике все время приходится изменить величины напряжения и тока. Поэтому вся электрическая энергия вырабатывается в виде переменного тока. Основным преимуществом переменного тока перед постоянным током в том, что в цепи переменного тока с помощью трансформаторов просто и экономично как повышением, так и понижением напряжения с одновременным повышением или понижением силы тока, так что передаваемая по цепи мощность остается практически неизменной. Это позволяет, пользуясь на электростанциях генераторами сравнительно невысокого напряжения (6…10 кВ), передавать энергию по проводом на большие расстояния при гораздо более высоком напряжении (до 400 кВ), и соответственно меньшей силе тока, благодаря чему значительно возрастает та мощность, которая может быть передана по проводом заданного сечения.

На месте потребления электрической энергии напряжение может быть понижено трансформатором до любой необходимо величины. Таким образом, главным преимуществом переменного тока является возможность получать при помощи трансформатора переменный ток различного напряжения: высокого – для передачи электроэнергии на большие расстояния, низкого – для питания потребителей.

Все электростанции мира вырабатывают переменный ток стандартной частоты 50 Гц. Исключением являются электростанции США, где принята частота 60 Гц.

Переменный ток низкой частоты известен с 30-х годов ХIХ века.

ПОНЯТИЕ О ГАРМОНИЧЕСКИХ ФУНКЦИЯХ НАПРЯЖЕНИЯ И ТОКА

Частным, но весьма важным для физических вообще и электрических в частно­сти применений является периодический процесс, представляющий собой гар­моническое колебание. В электротехнике и электронике довольно часто имеют дело с гармоническими токами и напряжениями. Напряжение, доступное всем через розетки электрической сети, является гармоническим колебанием. Лабораторные источники напряжения (так называемые генераторы стандартных сигналов), используемые для настройки и ремонта аппаратуры, про­ведения исследований, вырабатывают гармонические напряжения, параметры которых можно изменять в широких пределах. Немаловажно, что гармонический сигнал является как раз одним из простейших (тестовых) сигналов – учитывая, что любой сложный сигнал можно представить совокупностью гармо­нических колебаний. Таким образом, умение анализировать процессы в цепях, находящихся под воздействием гармонических напряжений и токов, открывает путь к анализу преобразования линейной цепью сигналов произвольной формы.

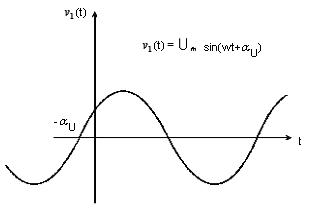
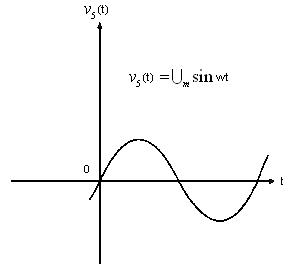
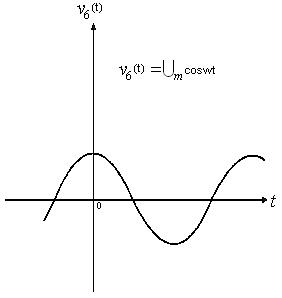
Если значения функции времени, например, напряжения 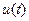, изменяются по синусоидальному или косинусоидальному закону (рис.1):

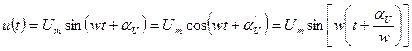
то такую функцию будем называть гармонической.

Здесь 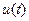– мгновенное значение функции напряжения в момент времени t;

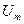- амплитуда или наибольшее значение гармонической функции. Размерность амплитуды определяется фи­зическими свойствами колебания: в частности, для тока это – Амперы, для напря­жения – Вольты.

- фаза или мгновенная фаза, измеряется в радианах или градусах;

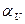- начальная фаза (при t=0) синусоидальной гармонической функции;

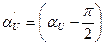- начальная фаза косинусоидальной функции;

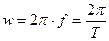- круговая или угловая частота. Единица измерения радиан в секунду – рад/с;

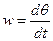- скорость изменения фазы;

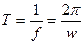- период. Единица измерения [c];

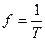- частота или число периодов в секунду. Единица частоты – 1 период в секунду называется Герц, [f] = Гц

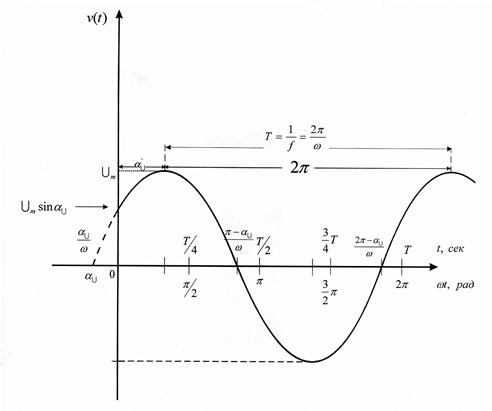
Рис.1

Функция времени называется периодической, если ее значения повторяются через определенные промежутки времени. Наименьший промежуток времени Т через который наблюдается повторение значений функции, называется периодом:

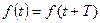
На рис.2, а изображена временная диаграмма гармонического колебания a(t), то есть, имеет место временное представле­ние гармонического колебания. Именно так выглядит гармоническое колебание на экране осциллографа (осциллограмма колебания). Но можно изобразить гармо­ническое колебание иначе, построив спектральные диаграммы, или спектрограм­мы, – амплитудную (рис.2, б – сверху) и фазовую (рис.2, б – снизу). На спектральных диаграммах по осям абсцисс откладывают частоту, а по осям орди­нат – значения амплитуды и начальной фазы гармонического колебания. Когда изображают гармонические колебания (в кратком произношении – гармоники) посредством спектральных диаграмм, говорят о частотном представлении коле­бательного процесса. Для наблюдения процессов во временном представлении используют осциллографы, отображающие осциллограммы колебаний. Для на­блюдений процессов в частотном представлении (спектрограмм) используют анализаторы спектров.

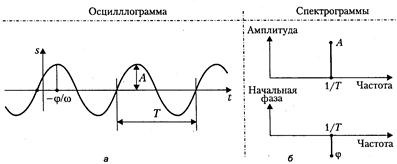
Рис.2

Начальная фаза 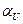отсчитывается от начала координат до ближайшего нулевого значения функции на нарастающем участке. При 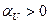нуль смещается влево от начала координат, при 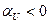смещается вправо.

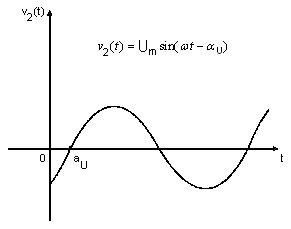
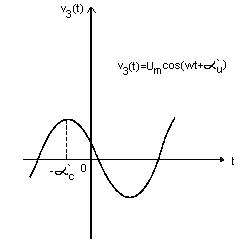
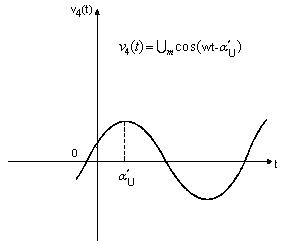
Если фазы θ₁ и θ₂ двух гармонических функци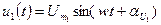й

и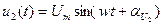

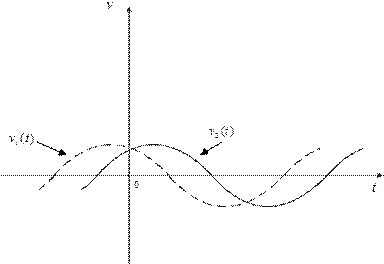
отличаются на угол 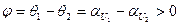, то говорят, что эти функции сдвинуты по фазе, причем функция 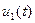опережает по фазе функцию 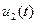на угол 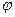. Графически, та функция 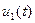у которой нулевые значения на нарастающем участке достигается раньше чем у другой - 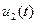, является опережающей по фазе:

Амплитуда и частота гармонических колебаний являются постоянными величи­нами. При сопоставлении разных гармонических колебаний основной интерес представляет то, как соотносятся между собой их фазовые углы, и таким образом, на первый план выходит разность фаз колебаний, или фазовый сдвиг одного ко­лебания по отношению к другому. Фазы ωt + φ₁, и ωt + φ₂ двух колебаний одина­ковой частоты ω растут с течением времени с одинаковой скоростью ω, однако их фазовый сдвиг не зависит ни от текущего времени, ни от выбора начала отсчета на временной оси: ωt + φ₁ – ωt – φ₂ = φ₁ – φ₂.

Описывая фазовые соотношения двух колебаний одинаковой частоты, говорят, что колебания синфазны (при нулевом фазовом сдвиге 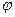=0), противофазны (если сдвиг по фазе составляет 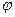= ± 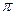), находятся в квадратуре (если фазы отличаются на 90°). Если разность фаз колебания А и колебания В положительна, использу­ют такие терминологические обороты: “колебание А опережает по фазе колеба­ние В” или “колебание В отстает по фазе от колебания А”. Условность этих фраз очевидна – опережение по фазе на 90° означает отставание на 270°. И то и другое утверждения справедливы.

Синусоидальные токи и напряжения обладают следующими свойствами:

1. Суммирование (или вычитание) синусоидальных функций, производимое по закону Кирхгофа дает синусоидальную функцию той же частоты:

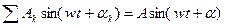
2. Дифференцирование и интегрирование синусоидальных функции производимое элементами L и C, дает также синусоидальную функцию той же частоты:

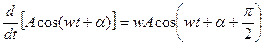
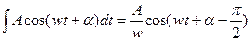
При описании интенсивности гармонических колебаний (гармонических токов и напряжений) наряду с амплитудой используют понятия действующего (сред­неквадратичного, эффективного) и средневыпрямленного значений. Действующее значение (А_д) находят вычислением квадратного корня от среднего за период зна­чения функции a(t), возведенной в квадрат:

.

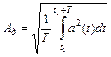Поскольку для периодического колебания результат интегрирования за интервал времени равный или кратный периоду не зависит от выбора начального значения промежутка интегрирования, можно данную формулу записать так:

.

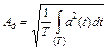Подставив сюда функцию 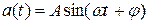, получаем соотношение действую­щего и амплитудного значений гармонического колебания:

.

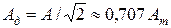Действующими значениями тока или напряжения удобно пользоваться при описа­нии эффектов, связанных с потреблением и преобразованием энергии. Действи­тельно, если по какому-либо резистору протекает гармонический ток, имеющий действующее значение I_д, то этим резистором будет потребляться (например, пере­ходить в тепло) такая же энергия, как при протекании через него постоянного тока того же значения. Следовательно, гармонический ток i(t) с действующим значени­ем I_д будет нагревать резистор так же, как постоянный ток равный I_д.

Надо иметь в виду, что шкалы большинства измерительных приборов, предна­значенных для измерения переменных токов и напряжений, градуируют в дейст­вующих значениях. Кстати, если колебание по форме отличается от гармониче­ского, например, является пилообразным, то при вычислении размаха колебания по показанию такого вольтметра надо использовать коэффициент пересчета, свя­зывающий амплитуду и действующее значение периодического колебания кон­кретной формы.

Частота напряжения электрической сети (f) равна 50 Гц. В сети с дейст­вующим значением напряжения равным 220 В амплитуда, соответственно, состав­ляет 310 В. Вольтметр переменного напряжения, подключенный к розетке бытовой элек­трической сети, покажет 220 В.

Если вычислить среднее за период значение гармонического колебания, оно бу­дет нулевым. Для описания уровня гармонического тока или напряжения иногда используют средневыпрямленное значение, представляющее собой интеграл за пе­риод от модуля периодической функции:

.

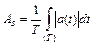Подставив в эту формулу функцию 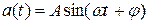, получим связь средневыпрямленного значения с амплитудным:

.

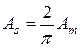Понятно, что для периодического колебания, отличающегося по форме от гармо­нического, коэффициент, стоящий перед амплитудой, будет иным.

Дата добавления: 2014-08-09; просмотров: 625; Нарушение авторских прав

Мы поможем в написании ваших работ!