Электрические цепи постоянного тока

2.1 Методы расчета электрических цепей постоянного тока.

В теории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализаэлектрических цепей, когда, например, известны конфигурация цепи, элементы и их параметры, а требуется определить токи, напряжения и мощности тех или иных участков. Ко второму типу относятся обратные задачи, в которых, например, заданы токи и напряжения на некоторых участках, а требуется найти конфигурацию цепи и выбрать ее элементы. Такие задачи называются задачами синтеза. Решение этих задач намного сложнее, чем задач анализа.

В практической электротехнике чаще встречаются задачи анализа, которые могут быть решены, например, при помощи законов Кирхгофа.

При помощи закона Ома и двух законов Кирхгофа можно рассчитать электрическую цепь любой сложности.

2.1.1 Метод расчета электрических цепей на основании закона Ома

Непосредственное решение уравнений цепи по законам Ома применяется при расчете простейших электрических цепей с одним источником ЭДС и различным способом соединения пассивных элементов – резисторов.

Предварительно осуществляется преобразование пассивных электрических цепей с последовательным, параллельным и смешанным соединением элементов, которое используется для упрощения расчетной схемы и уменьшения числа ее ветвей. Обычно к преобразованию линейных электрических цепей прибегают перед началом решения задачи с целью уменьшения числа расчетных уравнений.

Условием правильного преобразования схемы одной конфигурации в другую (если преобразуется часть схемы, не содержащая источников энергии) является энергетическая эквивалентность исходной и преобразованной схем. Эквивалентнымназывают преобразование, при котором токи, напряжения и, следовательно, мощности остальной части схемы не изменяются.

Кроме того, в тех участках схемы, которые не подвергались преобразованию, токи и напряжения должны также остаться прежними.

Основные виды преобразований пассивных электрических цепей

- Последовательное соединение резисторов – такое соединение участков электрической цепи, при котором через все ее участки проходит один и тот же ток. При последовательном соединении резисторов эквивалентное (общее) сопротивление цепи равно сумме сопротивлений отдельных резисторов:

R_э = R₁ + R₂ + … R_n. (1)

- При параллельном соединении резисторов эквивалентное (общее) сопротивление цепи равно:

. (2)

В качестве примера расчета электрической цепи на основании закона Ома рассмотрим расчет электрической цепи со смешанным соединением резисторов (рис. 1).

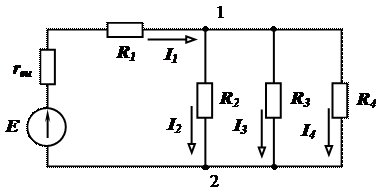
Целесообразно придерживаться следующего порядка расчета:

1. Выбрать и показать на схеме условно положительное направление токов.

2. Преобразовать участок с параллельным соединением

,

где , откуда .

3. Определить эквивалентное сопротивление

.

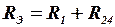4. Определить общее сопротивление цепи

.

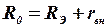5. По закону Ома для замкнутого контура определить ток

.

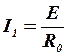6. Найти напряжение на параллельном участке из закона Ома

.

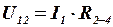7. Определить токи по закону Ома для параллельных участков

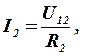
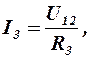
2.1.2 Метод расчета электрических цепей на основании законов Кирхгофа

Основным (универсальным) методом расчета электрических цепей является метод расчета с помощью законов Кирхгофа.

Расчет данным методом осуществляется в следующей последовательности:

1. На схему наносятся условные положительные направления токов в ветвях.

2. Выбирается направление обхода контуров для составления уравнений по второму закону Кирхгофа.

3. Составляются уравнения на основании первого и второго законов Кирхгофа. Общее число уравнений должно быть равно числу ветвей (n_в), т.е. числу неизвестных токов.

По первому закону Кирхгофа составляется на одно уравнение меньше, чем количество узлов (n_у), т.е. n_у – 1. Остальные уравнения составляются по второму закону Кирхгофа. Число их равно n_в – (n_у – 1).

4. Решается полученная система уравнений. После определения токов схемы напряжения на отдельных ее участках могут быть найдены по закону Ома.

В результате расчета может оказаться, что токи имеют отрицательные значения. Это означает, что действительные токи имеют противоположные направления, выбранные нами.

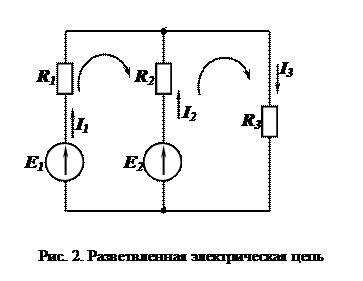Для разветвленной цепи (рис. 2), имеющей два узла (А и В), три ветви, т.е. три неизвестных тока I₁, I₂, I₃, при выбранных направлениях токов и направлениях обхода контуров, система уравнений, составленных по законам Кирхгофа, запишется в виде:

I₁ + I₂ - I₃ = 0;

Е₁ – Е₂ = I₁R₁ – I₂R₂;

Е₂ = I₂R₂ + I₃R₃.

При расчете цепей часто преобразуют отдельные участки схемы с помощью простейших эквивалентных преобразований.

После определения токов схемы напряжения на любых участках могут быть определены по закону Ома.

Недостатком метода является громоздкость решения, но уравнения Кирхгофа лежат в основе других методов расчета, позволяющих упростить расчет (сократить число уравнений).

2.1.3 Метод узловых потенциалов

Является одним из основных при расчете сложных электрических цепей.

Режим любой цепи полностью характеризуется уравнениями, составленными на основании первого и второго законов Кирхгофа. Но этот метод, как уже рассматривали, является очень трудоемким, ибо приходится решать систему уравнений с большим числом неизвестных.

Число уравнений, подлежащих решению, можно сократить, если пользоваться методом узловых потенциалов, основанным на применении первого закона Кирхгофа и закона Ома.

Для расчета цепи методом узлового напряжения (узловых потенциалов)необходимо:

а) в цепи произвольно назначить направления токов;

б) определить узловое напряжение:

;

произведение в числителе берется из знаком «+», если направление ЭДС не совпадает с направлением узлового напряжения;

в) определив узловое напряжение, можно найти токи во всех ветвях электрической цепи:

.

Если ток имеет отрицательное значение, то действительное его направление противоположно обозначенному на схеме.

2.1.4 Метод эквивалентного генератора

Этот метод удобен в том случае, когда необходимо определить изменение тока какой-либо одной ветви сложной цепи при изменении сопротивления этой ветви.

Сущность этого метода заключается в том, что ветвь сложной схемы, в которой необходимо определить ток, следует рассматривать как нагрузку для некоторого эквивалентного генератора, которым является вся остальная часть цепи, состоящая из источников и сопротивлений.

На рис. 3 представлена электрическая цепь, в которой выделена только одна ветвь АБ, ток которой требуется найти. Остальная часть цепи, содержащая источники и сопротивления, заключенная в прямоугольник, называется эквивалентным генератором, нагрузкой которого является сопротивление R.

ЭДС эквивалентного генератора равна напряжению 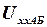на его зажимах при разомкнутой ветви АБ. Внутреннее сопротивление 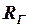эквивалентного генератора равно сопротивлению всей цепи относительно точек АБ (без ветви АБ) при условии, что все ЭДС источников, входящих в эквивалентный генератор, принимаются равными нулю, а на месте источников остаются включенными их внутренние сопротивления. После введения понятий об ЭДС эквивалентного генератора 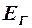и его внутреннем сопротивлении 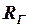схема (рис. 3) может быть заменена упрощенной схемой (рис. 4), из которой следует, что искомый ток I равен

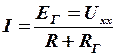. (3)

Итак, для определения тока Iв ветвях АБ необходимо:

- определить напряжение на зажимах разомкнутой цепи АБ;

- определить внутренне сопротивление 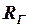всей цепи по отношению к зажимам АБ. Для этого все ЭДС цепи приравниваются нулю, а на местах источников оставляют их внутреннее сопротивление.

В частном случае, при (режим короткого замыкания), ток в ветви АБ равен

. (4)

Из формулы (4) вытекает простой способ экспериментального определения внутреннего сопротивления. Для этого необходимо замерить ЭДС эквивалентного генератора на зажимах разомкнутой ветви АБ и ток короткого замыкания при коротком замыкании этой ветви, тогда

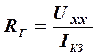. (5)

Исходя из этого, метод эквивалентного генератора часто называют методом холостого хода и короткого замыкания. Из формулы (3) следует, что, задавая различные значения сопротивлению 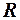ветви АБ, можем найти соответствующие значения токов в этой ветви. Это является важным преимуществом МЭГ по сравнению с другими методами.

Применение метода эквивалентного генератора позволяет достаточно просто решить важный вопрос о максимальной мощности, которую может потреблять любая ветвь данной сложной цепи.

2.1.5 Метод контурных токов.

Этот метод является одним из наиболее часто используемых методов расчета сложных линейных электрических цепей. МКТ позволяет рассчитать сложную электрическую цепь с помощью меньшего числа уравнений, чем число уравнений, полученных на основании законов Кирхгофа. В этом заключается основное преимущество МКТ. При расчете сложных электрических цепей методом контурных токов составляются лишь уравнения по второму закону Кирхгофа для независимых контуров, т.е. по сравнению с методом, основанном на законах Кирхгофа, число уравнений уменьшается на .

Существо МКТ рассмотрим на примере схемы рис. 5, состоящей из шести ветвей и четырех узлов, т.е. и . Для расчета этой схемы по законам Кирхгофа понадобилось бы шесть уравнений с шестью неизвестными токами. В нашем примере три независимых контура, следовательно, необходимо составить и решить систему из трех уравнений.

Контурным током называется условный, расчетный ток, протекающий последовательно через все элементы данного контура. На рис. 5 все три контурных тока I₁₁,I₂₂,I₃₃ показаны сплошной стрелкой, направление обхода обозначено пунктирными стрелками. Действительные токи ветвей, которые входят только в один контур, равны контурным токам (так, например, I₁= I₁₁). Действительные токи в ветвях схемы, являющейся общей для двух контуров, следует определять как алгебраические суммы контурных токов, протекающих через эти ветви (например I₃= I₁₁- I₃₃).

 

Порядок расчета цепей МКТ:

- выбираем произвольно направление контурных токов;

- направления обхода берем совпадающим с направлением контурных токов;

- составляем уравнения по второму закону Кирхгофа, причем, число уравнений системы равно числу независимых контуров;

- в левой части каждого уравнения берется алгебраическая сумма ЭДС, входящая в данный контур. При этом положительными берутся те ЭДС, направления которых совпадают с направлением контурного тока данного контура;

- в правой части происходит падение напряжений от контурных токов, протекающих по сопротивлениям того контура, для которого составлено данное уравнение. Падение напряжения от контурного тока данного контура берется со знаком «плюс» (направления обхода контуров совпадают с направлением контурных токов). Падения напряжения от контурных токов смежных контуров берутся положительными, если их направления совпадают в смежных сопротивлениях с направлением контурного тока данного контура;

- решается система уравнений и находятся действительные токи в ветвях:

(1-й контур) Е₁ + Е₃ = I₁₁(R₁ + R₄ + R₃) – I₃₃R₃ – I₂₂R₄ ;

(2-й контур) - Е₂ = I₂₂(R₂ + R₅ + R₄) – I₁₁R₄ – I₃₃R₅ ; (6)

(3-й контур) - Е₃ = I₃₃(R₃ + R₅ + R₆) – I₁₁R₃ – I₂₂R₅.

Систему уравнений, содержащую неизвестные контурные токи, удобно решать при помощи определителей.

Введем обозначения:

 

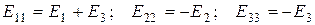- контурные ЭДС, равные алгебраической

сумме ЭДС, входящих в данный контур;

 

- собственные (пол-

ные) сопротивления

контуров;

 

- взаимные сопротивления (со-

противления смежных ветвей

между контурами).

Тогда система уравнений (1) примет вид:

 

(2)

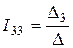(3)

 

где D - главный определитель системы (2)

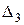, , - частные определители системы, причем:

 

 

 

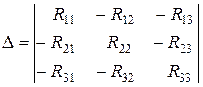
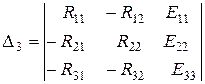
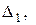
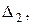
Выражения (3) для контурных токов можно представить в более удобном для анализа виде, если определители разложить по элементам столбцов, содержащих контурные ЭДС.

Проделав это, получим:

 

;

 

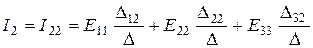; (4)

 

где D_кm – алгебраические дополнения (к=1, 2, 3; m=1, 2, 3), получаемые из главного определителя путем вычеркивания в нем к – той строки и m – го столбца и умножения вновь полученного определителя на (-1)^к+m.

Например,

;

 

;

 

 

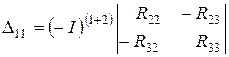После подсчета значений контурных токов по формулам (3) или (4) можно определить действительные токи схемы (рис.5)

Преимущества и особенности метода:

1)МКТ позволяет уменьшить количество уравнений по сравнению с МЗК вдвое.

2)Кроме того, МКТ позволяет вести расчет в стандартной форме, т.е. полный расчет можно запрограммировать и осуществить с помощью ЭВМ.

3)МКТ и МУП как бы дополняют друг друга. Если МКТ применяются к независимым контурам цепи, то МУП – к независимым узлам цепи. Вопрос о том, каким методом целесообразнее воспользоваться, зависит от конфигурации цепи, а именно от того, что является меньшим, – число независимых контуров или число независимых узлов 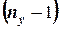. В первом случае лучше воспользоваться методом контурных токов, а во втором – методом узловых потенциалов.

2.1.6 Метод наложения (суперпозиции).

 

Если цепь имеет несколько источников питания, то для расчета этих цепей можно применить метод суперпозиции (метод наложения). Этот метод использует принцип независимости действия ЭДС и основан на том, что ток в любой ветви электрической цепи равен алгебраической сумме токов, создаваемых в этой ветви каждой ЭДС в отдельности.

Вычисление сложных цепей с несколькими источниками питания по методу суперпозиции можно осуществить следующим образом:

а) сложную цепь заменяют несколькими цепями, каждая из которых имеет один источник в элементарной цепи, другие заменяют сопротивлениями, которые равны внутренним сопротивлениям источников;

б) рассчитывают элементарные цепи, определяя величины и направления токов в каждой ветви;

в) в каждой ветви находят действительные токи как алгебраическую сумму соответствующих токов, т.е. слагаемыми действительного тока являются токи этой ветви в элементарных цепях.

Для примера можно вычислить цепь, приведенную на рис. 6. В первом случае рассмотрим цепь без ЭДС Е₂. Внутреннее сопротивление этой ЭДС равно нулю. Все токи будем помечать штрихом, то есть

, , .

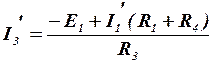Дальше можно рассмотреть цепь без источника Е₁ , но учесть его внутреннее сопротивление R₁. Токи будем помечать двумя штрихами:

 

, , .

Действительные токи являются суммой соответствующих токов элементарных цепей, т.е.

, , .

Принцип наложения справедлив не только для контурных токов, но и для тока в любой ветви, так как можно всегда выбрать совокупность контуров так, что интересующая вас ветвь войдет только в один контур. Это непосредственно вытекает также из линейности системы уравнений, записанных в отношении истинных токов в ветвях по законам Кирхгофа. Следует иметь в виду, что принцип наложения не применим для квадратичных форм, каковыми являются выражения для мощности.

Преимущества и особенности метода:

1)Метод наложения, основанный на принципе наложения, позволяет расчленить сложную задачу на ряд более простых, в каждой из которых в рассматриваемой сложной цепи действует только одна ЭДС, а все остальные источники энергии предполагаются отсутствующими. При этом все другие источники ЭДС должны быть замкнуты накоротко с сохранением в ветвях их внутренних сопротивлений.

2) Метод наложения позволяет оценить, какое значение имеют отдельные ЭДС в создании токов в ветвях цепи. Метод нашел широкое применение в расчете линейных цепей с несинусоидальными и импульсными ЭДС. Применение метода наложения в этих случаях позволяет достаточно просто рассчитать и проанализировать процессы, происходящие в электрических цепях.

3) Следует отметить, что как метод расчета цепей постоянного тока принцип наложения неудобен вследствие своей громоздкости по сравнению с другими методами и поэтому применяется редко.

2.2 Электрическая мощность и энергетический баланс в электрических цепях. Потенциальная диаграмма.

 

Согласно закону сохранения энергии, работа и мощность источников электрической энергии какой-либо цепи должны равняться работе и мощности всех потребителей этой цепи:

или ,

где - мощность, развиваемая источником энергии,

- мощность, потребляемая нагрузкой (приемником),

- алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия ЭДС 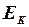и соответствующего тока 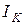совпадают, в противном случае слагаемое отрицательно;

- арифметическая сумма; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.

Для схемы (рис. 7) баланс мощностей можно записать:

 

 

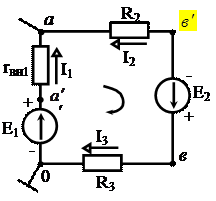Рис 7. Пример схемы электрической цепи для выражения баланса мощностей

Баланс мощностей используется для проверки правильности расчета токов. Если токи вычислены верно, должно получиться тождество. Реально можно полагать, что токи найдены правильно, если относительная погрешность:

не превышает ±5 %.

Потенциальной диаграммой электрической цепи называется диаграмма распределения потенциалов в ней относительно точки, потенциал которой условно принят равным нулю.

Потенциальные диаграммы широко используются при анализе работы электрических и электронных схем (схемы с электроннолучевыми трубками, схемы с электронными лампами и полупроводниковыми приборами, логические схемы и т.д.).

Рассмотрим расчет потенциалов и построение потенциальной диаграммы на примере схемы ЭЦ, изображенной на рис. 15.

Обозначим на схеме точки, потенциалы которых необходимо определить. Направление обхода контура выберем по часовой стрелке. Примем потенциал . Тогда:

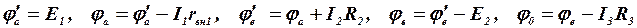
Потенциальная диаграмма имеет вид (рис. 16).

 

 

Рис 16. Потенциальная диаграмма

 

Проверка правильности расчета электрической цепи

Если токи вычислены верно, то, начав построение потенциальной диаграммы с точки с потенциалом, равным нулю, должны обойдя контур, вернуться в ту же точку с потенциалом так же равным нулю.

 

 

 

Дата добавления: 2014-08-09; просмотров: 2046; Нарушение авторских прав

Мы поможем в написании ваших работ!