
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Тема 1. ПРОСТЫЕ ПРОЦЕНТЫ
Финансово – экономические расчеты (финансовая математика, финансовые вычисления) – область знаний, в которой излагается методология количественного финансового анализа условий и результатов финансово-кредитных и коммерческих сделок. Они представляют собой совокупность методов и приемов определения изменения стоимости денег, происходящего вследствие их возвратного движения (предоставления в долг).
Процент рассматривается как плата за пользование заемными средствами, так и показатель доходности любого вложения капитала. Причем вложение капитала может в действительности и не состояться.
Условные обозначения:
Р - величина первоначального капитала, (ссуды, долга, кредита и т.д.);
S – наращенная сумма или конечная стоимость капитала, которая получена прибавлением к первоначальной величине начисленных процентов;
n – число лет наращения;
i – годовая процентная ставка (обычно измеряется десятичной дробью);
t – срок финансовой операции, выраженный в днях;
m – срок операции, выраженный в месяцах;
К – число дней в году (365, 366 или 360);
d – годовая учетная ставка;
I – процентный доход или процент, как величина дохода от сделки.
Сумма процентного дохода, начисленного за весь период:
I = 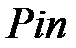 . (1.1)
. (1.1)
Наращенная сумма декурсивных процентов:
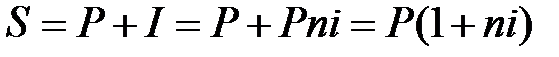 , (1.2)
, (1.2)
где (1 + ni) – множитель наращения простых декурсивных процентов.
Если срок финансовой сделки выражен в месяцах, то величина наращенной суммы определяется по формуле:
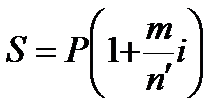 , (1.3)
, (1.3)
где 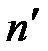 - 12 месяцев.
- 12 месяцев.
Когда срок финансовой сделки выражается в днях, то наращенная сумма определяется по формуле:
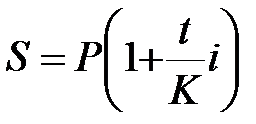 . (1.4)
. (1.4)
Если необходимо определить процентный доход, а срок финансовой сделки определяется в месяцах или днях, то:
доход за один месяц 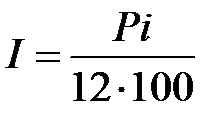 ; (1.5)
; (1.5)
доход за m – месяцев 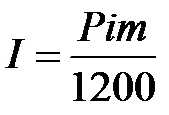 ; (1.6)
; (1.6)
доход за один день 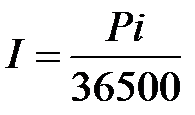 ; (1.7)
; (1.7)
доход за t – дней 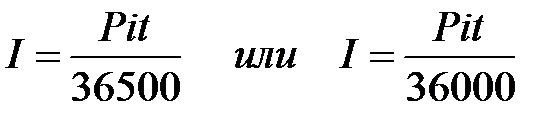 . (1.8)
. (1.8)
Эти формулы справедливы если процентная ставка выражается в процентах, если ставка выражена в виде десятичной дроби, то знаменатель необходимо разделить на 100.
Когда применяется переменная процентная ставка, дискретно изменяющаяся во времени, то наращенная сумма находится по формуле:
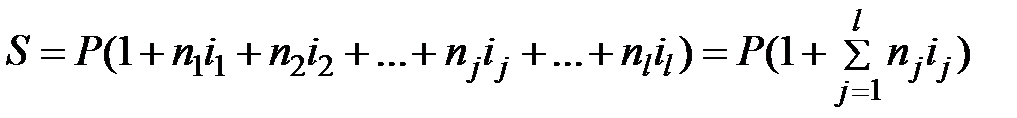 . (1.9)
. (1.9)
При антисипативном методе начисления процентов за базу принимается сумма возврата долга, тогда наращенная сумма определяется по формуле:
S= 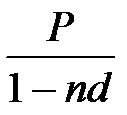 ,(1.10)
,(1.10)
где d – учетная ставка, выраженная десятичной дробью,
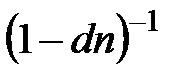 - множитель наращения простых антисипативных процентов.
- множитель наращения простых антисипативных процентов.
Если d выражается в процентах, то формула примет вид:
S= 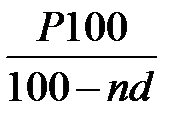 . (1.11)
. (1.11)
При математическом дисконтировании современная величина суммы S находится по формуле 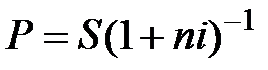 , (1.12)
, (1.12)
где (1 + ni)-1 является дисконтным множителем.
При банковском дисконтировании сумма, получаемая клиентом в результате учета долгового обязательства, находится по формуле:
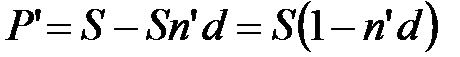 , (1.13)
, (1.13)
где n' – временной интервал между датой учета и датой погашения векселя.
Дисконтный множитель здесь равен ( 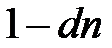 ). Учет посредством учетной ставки чаще всего осуществляется при временной базе K=360 дней, число дней финансовой операции обычно берется точным. Дисконт
). Учет посредством учетной ставки чаще всего осуществляется при временной базе K=360 дней, число дней финансовой операции обычно берется точным. Дисконт 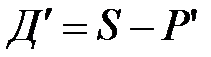 .
.
Срок финансовой сделки и величина процентной ставки находятся из формул наращенных сумм:
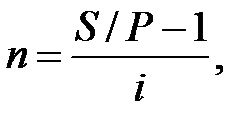
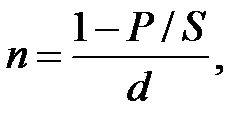 (1.14)
(1.14)
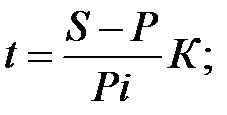
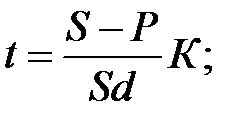 (1.15)
(1.15)
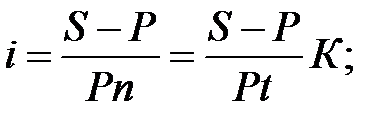
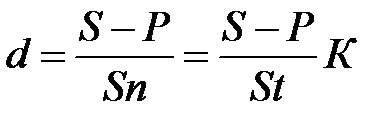 . (1.16)
. (1.16)
Задачи для самостоятельного решения
1.1 Банк выдал клиенту кредит в сумме 200000 руб. на 2 года, при процентной ставке 14,6 %. Определите, какую сумму должен вернуть клиент банку и процентный доход банка.
1.2 Определите проценты и сумму накопленного долга, если ссуда равна 700 тыс.руб., начисляются простые декурсивные проценты по ставке 15 % годовых, при сроке ссуды: 45 дней; 90 дней; 6 месяцев; 10 месяцев; 1 год.
1.3 Ссуда выдана сроком на: 30 дней, 100 дней; 4 месяца; 8 месяцев; 1 год. По данным таблицы 1.1. Определить сумму к возврату ссуды и процентный доход, если при расчетах использовалась: а) процентная ставка; б) учетная ставка.
Таблица 1.1 – Размер ссуды и ставка
| Вариант | Ссуда, тыс. руб. | Ставка, % | Вариант | Ссуда, тыс. руб. | Ставка, % |
| 16,0 | 17,4 | ||||
| 18,5 | 15,0 | ||||
| 16,3 | 16,2 | ||||
| 14,9 | 17,0 | ||||
| 15,7 | 15,9 | ||||
| 19,0 | 15,2 | ||||
| 18,0 | 16,4 | ||||
| 14,1 | 15,2 | ||||
| 13,7 | 14,9 | ||||
| 18,2 | 16,4 | ||||
| 19,7 | 14,8 | ||||
| 14,8 | 17,5 | ||||
| 13,7 | 16,9 | ||||
| 15,9 | 15,7 | ||||
| 16,8 | 18,5 |
1.4 При известной годовой ставке простых процентов определить через сколько лет начальная сумма увеличится: в 1,2 раза; 1,5 раза; 1,8 раза; в 2 раза; 2,5 раза; в 3 раза; в 4 раза; в 5 раз. Как изменятся сроки ссуды, если при расчетах также использовалась простая учетная ставка.
Таблица 1.2 – Размер ставки, по которой производится начисление
| Вариант | Ставка, % | Вариант | Ставка, % |
| 16,0 | 17,4 | ||
| 14,5 | 15,0 | ||
| 16,3 | 16,2 | ||
| 14,9 | 17,0 | ||
| 15,7 | 15,9 | ||
| 14,0 | 15,2 | ||
| 18,0 | 16,4 | ||
| 14,1 | 15,2 |
Продолжение таблицы 1.2
| Вариант | Ставка, % | Вариант | Ставка, % |
| 13,7 | 14,9 | ||
| 16,2 | 16,4 | ||
| 15,7 | 14,8 | ||
| 14,8 | 17,5 | ||
| 13,7 | 16,9 | ||
| 15,9 | 15,7 | ||
| 16,8 | 15,5 |
1.5 Банк выдал клиенту кредит. Определите сумму, подлежащую возврату по английской, французской и германской практике по данным таблицы 1.3
Таблица 1.3 – Параметры кредитных сделок
| Вариант | Дата выдачи кредита | Срок возврата | Процентная ставка, % | Сумма основного долга, руб. | Вариант | Дата выдачи кредита | Срок возврата | Процентная ставка, % | Сумма основного долга, руб. |
| 10.01 | 20.08 | 10,2 | 16.01 | 11.09 | 13,4 | ||||
| 19.01 | 30.10 | 14,0 | 1.02 | 13.08 | 11,0 | ||||
| 5.02 | 18.09 | 12,6 | 28.03 | 30.10 | 18,5 | ||||
| 9.01 | 1.06 | 18,0 | 12.02 | 5.12 | 14,3 | ||||
| 30.01 | 10.11 | 14,9 | 14.03 | 5.06 | 20,4 | ||||
| 24.03 | 15.09 | 10,0 | 16.01 | 26.10 | 17,0 | ||||
| 16.02 | 20.11 | 14,3 | 11.04 | 24.11 | 18,9 | ||||
| 18.03 | 3.12 | 18,7 | 9.01 | 12.09 | 12,0 | ||||
| 16.04 | 23.10 | 21,2 | 6.04 | 7.12 | 14,3 | ||||
| 3.01 | 19.10 | 13,0 | 5.02 | 6.10 | 16,7 | ||||
| 18.01 | 19.05 | 16,5 | 7.01 | 5.05 | 10,9 | ||||
| 12.02 | 19.11 | 13,7 | 12.02 | 14.12 | 13,5 | ||||
| 2.03 | 14.07 | 12,0 | 24.02 | 16.09 | 21,3 | ||||
| 10.04 | 17.12 | 16,2 | 2.01 | 24.11 | 16,0 |
1.6 Движение средств на счете характеризуется следующими данными: 09.01 поступило 350000 рублей, 18.04 снято 45000 рублей, 28.08 поступило 130000 рублей, 7.10 снято 74000 рублей, 27.11 поступило 95000 рублей. Найдите сумму на счете на конец года. Процентная ставка 11 % годовых. При расчетах использовалась английская практика.
Методические указания
1) Процентный делитель (дивизор) определяется по формуле:
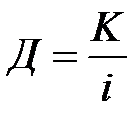 .
.
2) Определим процентные числа за j- тый период (таблица 1.4)
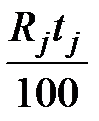 , j = 1, 2, …, l .
, j = 1, 2, …, l .
Таблица 1.4 – Определение сумм процентных чисел
| Дата | Движение средств, тыс. руб. | Остаток ( 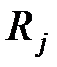 ), тыс. руб. ), тыс. руб.
| Срок (  ) )
| Процентное число ( 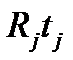 ), тыс. руб. ), тыс. руб.
|
| 09.01 | ||||
| 18.04 | ||||
| 28.08 | ||||
| 07.10 | ||||
| 27.11 | ||||
| 31.12 | - | - | - | |
| Итого | - | - |
3) Найдем сумму процентов за весь период:
 .
.
1.7 Движение средств на счете характеризуется данными представленными в таблице 1.5. Найдите сумму на счете на конец года, если процентная ставка составляет 9,5 % годовых. При расчетах использовалась французская практика.
Таблица 1.5 – Движение средств на счете
| Вариант | Сумма на счете на 10.01, тыс. руб. (открытие счета) | Движение средств на счете («+» поступление; «–» выбытие) | |||||
| 20.03 | 19.04 | 5.06 | 10.08 | 19.10 | 6.12 | ||
| +800 | -680 | -120 | +300 | -90 | +270 | ||
| -200 | -130 | -90 | +280 | +80 | -100 | ||
| -190 | -320 | +180 | -410 | +390 | +110 | ||
| -80 | +120 | -20 | +215 | +80 | -90 | ||
| +200 | +180 | -310 | +90 | +110 | -290 | ||
| -350 | -120 | +240 | +420 | -370 | +100 | ||
| -450 | +200 | +280 | -370 | +130 | -90 | ||
| +400 | +190 | +210 | -150 | -205 | +95 | ||
| -280 | +290 | +110 | -170 | -85 | +95 | ||
| +130 | +310 | -150 | -300 | +290 | +80 | ||
| +220 | +300 | +200 | -150 | -50 | +90 | ||
| +110 | +205 | -280 | -200 | +80 | +130 | ||
| -620 | -100 | +260 | +505 | -490 | +320 | ||
| -480 | -390 | +190 | +210 | +520 | -290 | ||
| +170 | -700 | -180 | +380 | +250 | -480 |
Продолжение таблицы 1.5
| Вариант | Сумма на счете на 10.01, тыс. руб. (открытие счета) | Движение средств на счете («+» поступление; «–» выбытие) | |||||
| 20.03 | 19.04 | 5.06 | 10.08 | 19.10 | 6.12 | ||
| -380 | -800 | +510 | +290 | +500 | -710 | ||
| +130 | -90 | -200 | +300 | -150 | +250 | ||
| -130 | -210 | +200 | -310 | +205 | -150 | ||
| +190 | -90 | -170 | -100 | +280 | +180 | ||
| +130 | -320 | -270 | +180 | +320 | -240 | ||
| -250 | +310 | -200 | +450 | -130 | +150 | ||
| -120 | +180 | +120 | -210 | -225 | +190 | ||
| +110 | -210 | -255 | +185 | -325 | +200 | ||
| +100 | -200 | +380 | -470 | -170 | +270 | ||
| -280 | -150 | +295 | +185 | -80 | -100 | ||
| -170 | +180 | +200 | -250 | +80 | +150 | ||
| -200 | +50 | -180 | +300 | -450 | -100 | ||
| -150 | +210 | -370 | -180 | +205 | +175 | ||
| +180 | +50 | -280 | +310 | -420 | +170 | ||
| -100 | +295 | -315 | -185 | +275 | -325 |
1.8 Банк предлагает клиенту следующие условия срочного годового депозита: в первом квартале процентная ставка 8 % годовых, каждые следующие три месяца ставка повышается на 0,8 %. Определите наращенную за год сумму 287000 рублей.
1.9 Контракт предусматривает следующий порядок начисления процентов: первые пять месяцев ставка – 10 %, в каждом последующем месяце ставка повышается на 0,5 %. Необходимо определить множитель наращения за: полгода; один года.
1.10 Клиентом в банке 19 февраля открыт счет на сумму 400000 рублей, при ставке 9,5 % годовых. 10.04 снято 118000 рублей, 24.07 внесено 224000 рублей, 7.09 снято 97000 рублей, 18.11 внесено 109000 рублей, а в конце года счет был закрыт. Какую сумму получит клиент, если 1.10 процентная ставка была повышена до 10,5 %.
1.11 Фирма получила кредит с оговоренной суммой возврата (таблица 1.6). Определите процентную и учетную ставку, если срок кредита составляет: 60 дней; 120 дней; 5 месяцев; 8 месяцев; 1 год (К = 360).
Таблица 1.6 – Сумма выдачи и возврата кредита
| Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. | Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. |
Продолжение таблицы 1.6
| Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. | Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. |
1.12 Фирма планирует получение кредита в сумме 150000 рублей, при условии возврата 200000 рублей. На какой срок фирма может взять кредит, если процентная ставка равна: 9 %; 14 %; 19 %; 25%.
1.13 По данным таблицы 1.7, определить на какой срок (в днях и годах) была выдана ссуда, если использовалась: 1) простая процентная ставка; 2) простая учетная ставка; в размере: 10,0%; 12,5%; 13,0%; 14,9%; 15,7%; 17,8%.
Таблица 1.7 – Сумма выдачи и возврата кредита
| Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. | Вариант | Первоначальная сумма, тыс. руб. | Сумма возврата, тыс. руб. |
1.14 Клиентом в банке взят кредит под 18 % годовых. В конце периода клиент должен выплатить определенную сумму (таблица 1.8). Определите процентный доход и сумму кредита, если срок кредита составляет: 65 дней; 90 дней; 110 дней; 4 месяца; 9 месяцев; 1 год (К = 365).
Таблица 1.8 – Сумма возврата кредита
| Вариант | Сумма возврата кредита, тыс. руб. | Вариант | Сумма возврата кредита, тыс. руб. |
1.15 На какой срок фирма может взять кредит в банке в размере 190000 рублей с условием, что сумма возврата кредита не превысит 220000 рублей, если банк применит учетную ставку в размере: 10 %; 15 %; 21 %. (Временная база – 365 дней).
1.16 Банк предоставил клиенту ломбардный кредит сроком на 3 месяца с 7.03 по 7.06 под залог акций. Сумма кредита равна 75 % от курсовой стоимости акций. Определите размер кредита, полученного клиентом в момент его обращения в банк, с учетом того, что проценты и комиссионные удерживаются из суммы выдаваемого кредита, по условиям, представленным в таблице 1.9.
Таблица 1.9 – Условия ломбардного кредита
| Вариант | Количество акций | Курсовая стоимость одной акции, руб. | Процентная ставка, % | Процент за обслуживание кредита | Вариант | Количество акций | Курсовая стоимость одной акции, руб. | Процентная ставка, % | Процент за обслуживание кредита |
| 14,0 | 0,60 | 15,0 | 0,60 | ||||||
| 14,5 | 0,65 | 16,5 | 0,65 | ||||||
| 18,0 | 0,70 | 15,5 | 0,70 | ||||||
| 18,5 | 0,75 | 19,5 | 0,75 | ||||||
| 12,0 | 0,80 | 17,0 | 0,80 | ||||||
| 20,0 | 0,85 | 20,5 | 0,85 | ||||||
| 24,0 | 0,90 | 20,0 | 0,90 | ||||||
| 16,0 | 0,95 | 19,5 | 0,95 | ||||||
| 17,5 | 1,00 | 16,0 | 1,00 |
Продолжение таблицы 1.9
| Вариант | Количество акций | Курсовая стоимость одной акции, руб. | Процентная ставка, % | Процент за обслуживание кредита | Вариант | Количество акций | Курсовая стоимость одной акции, руб. | Процентная ставка, % | Процент за обслуживание кредита |
| 13,5 | 1,05 | 18,5 | 1,05 | ||||||
| 21,0 | 1,10 | 17,0 | 1,10 | ||||||
| 19,0 | 1,15 | 13,5 | 1,15 | ||||||
| 17,0 | 1,20 | 21,0 | 1,20 | ||||||
| 19,5 | 1,25 | 13,5 | 1,25 |
1.17 Ссуда в размере 150000 руб. выдана 20.03 под 19 % годовых. Ее нужно погасить 15.11. Определите наращенную сумму при условии, что проценты начисляются по простой учетной ставке.
1.18 Предоставлен потребительский кредит на 12 месяцев. Определите сумму возврата кредита, используя различные варианты расчета. Составьте план погашения потребительского кредита.
Таблица 1.10 – Варианты потребительского кредита
| Вариант | Сумма кредита, руб. (Р) | Процентная ставка, % (i) | Вариант | Сумма кредита, руб. (Р) | Процентная ставка, % (i) |
| 15,0 | 12,5 | ||||
| 15,5 | 13,0 | ||||
| 16,0 | 13,5 | ||||
| 16,5 | 14,0 | ||||
| 17,0 | 14,5 | ||||
| 17,5 | 15,0 | ||||
| 18,0 | 15,5 | ||||
| 18,5 | 16,0 | ||||
| 19,0 | 16,5 | ||||
| 19,5 | 17,0 | ||||
| 20,0 | 17,5 | ||||
| 20,5 | 18,0 | ||||
| 11,0 | 18,5 | ||||
| 11,5 | 19,0 | ||||
| 12,0 | 19,5 |
Методические указания:
1) Сумма начисленных процентов за каждый период:
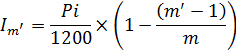
где:
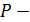 первоначальная сумма долга, руб.
первоначальная сумма долга, руб.
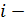 процентная ставка, %.
процентная ставка, %.
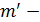 порядковый номер периода начисления процентов и выплаты основного долга.
порядковый номер периода начисления процентов и выплаты основного долга.
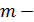 число периодов начислений процентов и выплат основного долга.
число периодов начислений процентов и выплат основного долга.
2) Выплата основного долга за один период:
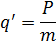
3) Общая сумма начисленных процентов за весь период:
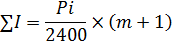
4) Вспомогательная таблица для расчетов:
Таблица 1.11 - План погашения кредита
| Месяц | Непогашенная сумма основного долга, руб. | Процентный платеж, руб. | Месячная выплата основного долга, руб. | Месячная сумма всей погасительной задолженности, руб. |
| - | - | - | ||
| Итого | - |
1.19 Вексель номинальной стоимостью 150000 руб. со сроком погашения 6.09 учтен 6.06 по учетной ставке 11,0 % годовых. Найдите дисконтированную величину векселя и сумму дисконта.
1.20 Вексель учтен 10.04 со сроком погашения 10.07. Определите номинальную стоимость векселя, если процентная ставка дисконтирования – 7,5 % годовых, а должник получил 10.04 – 248750 рублей.
Вопросы для самоконтроля
1. Дайте определение процентов и процентной ставки.
2. Какие виды процентных ставок применяются в финансовых расчетах и в чем их различие?
3. Как определяется наращенная сумма по формулам простых процентов?
4. Какие варианты расчета простых процентов применяются в мировой практике?
5. Что понимается под дисконтированием? Охарактеризуйте виды дисконтирования?
6. Как определяется современная стоимость платежа при применении математического и банковского дисконтирования?
7. Найдите срок финансовой сделки и величину процентной ставки из формул наращенных сумм по простым процентам.
| <== предыдущая страница | | | следующая страница ==> |
| Консолидация платежей | | | Тема 2. СЛОЖНЫЕ ПРОЦЕНТЫ |
Дата добавления: 2014-09-08; просмотров: 915; Нарушение авторских прав

Мы поможем в написании ваших работ!